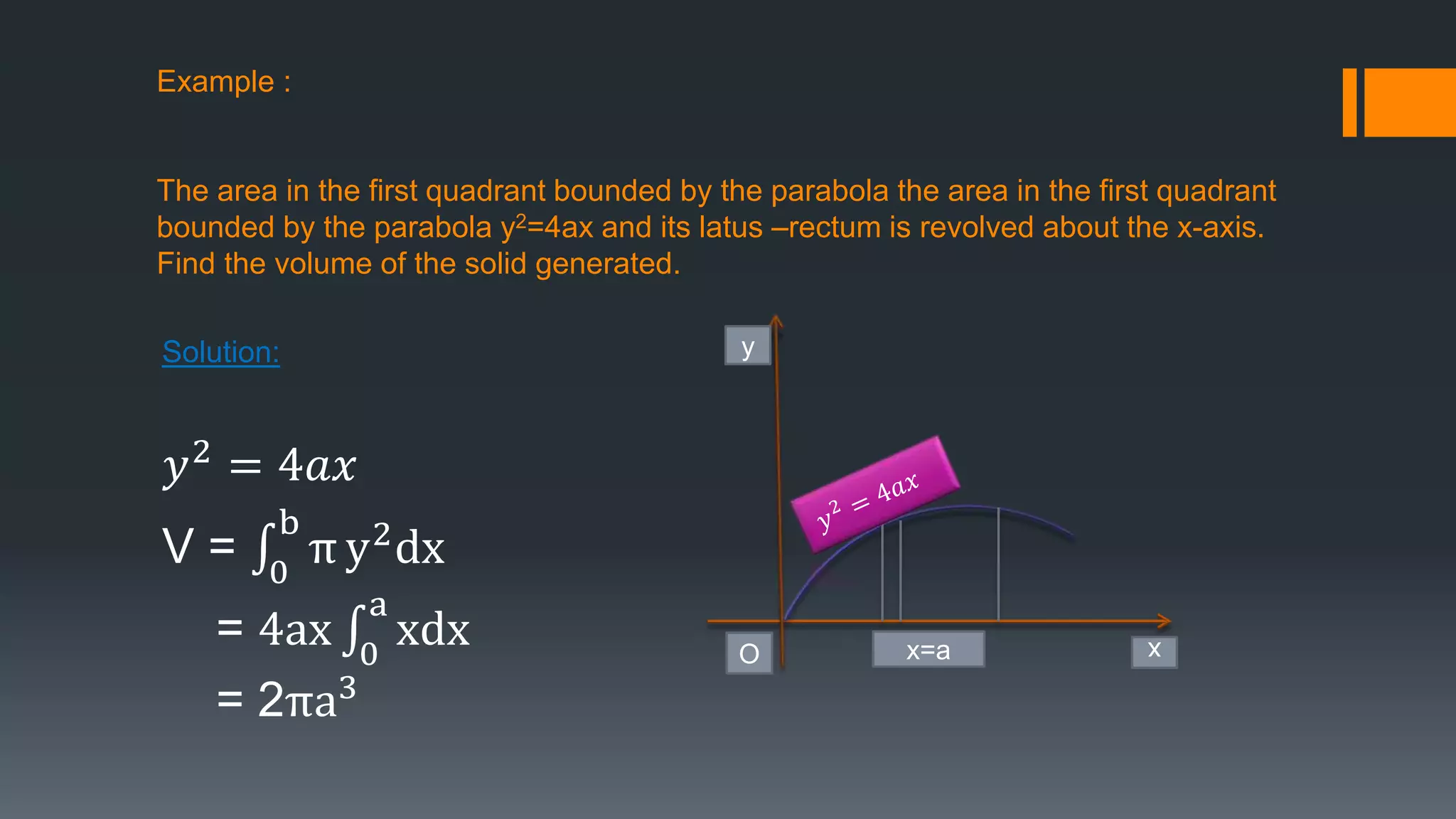
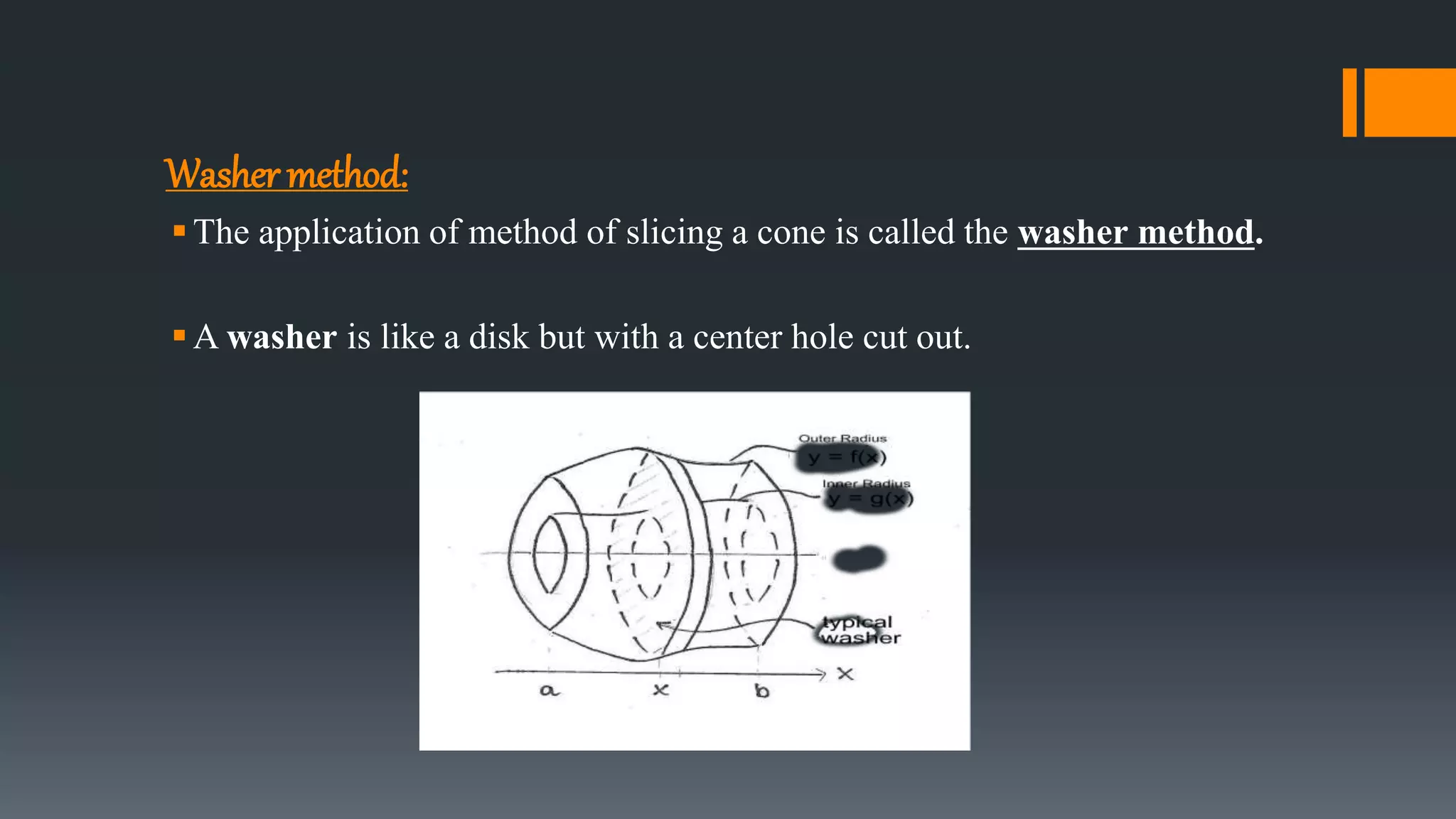
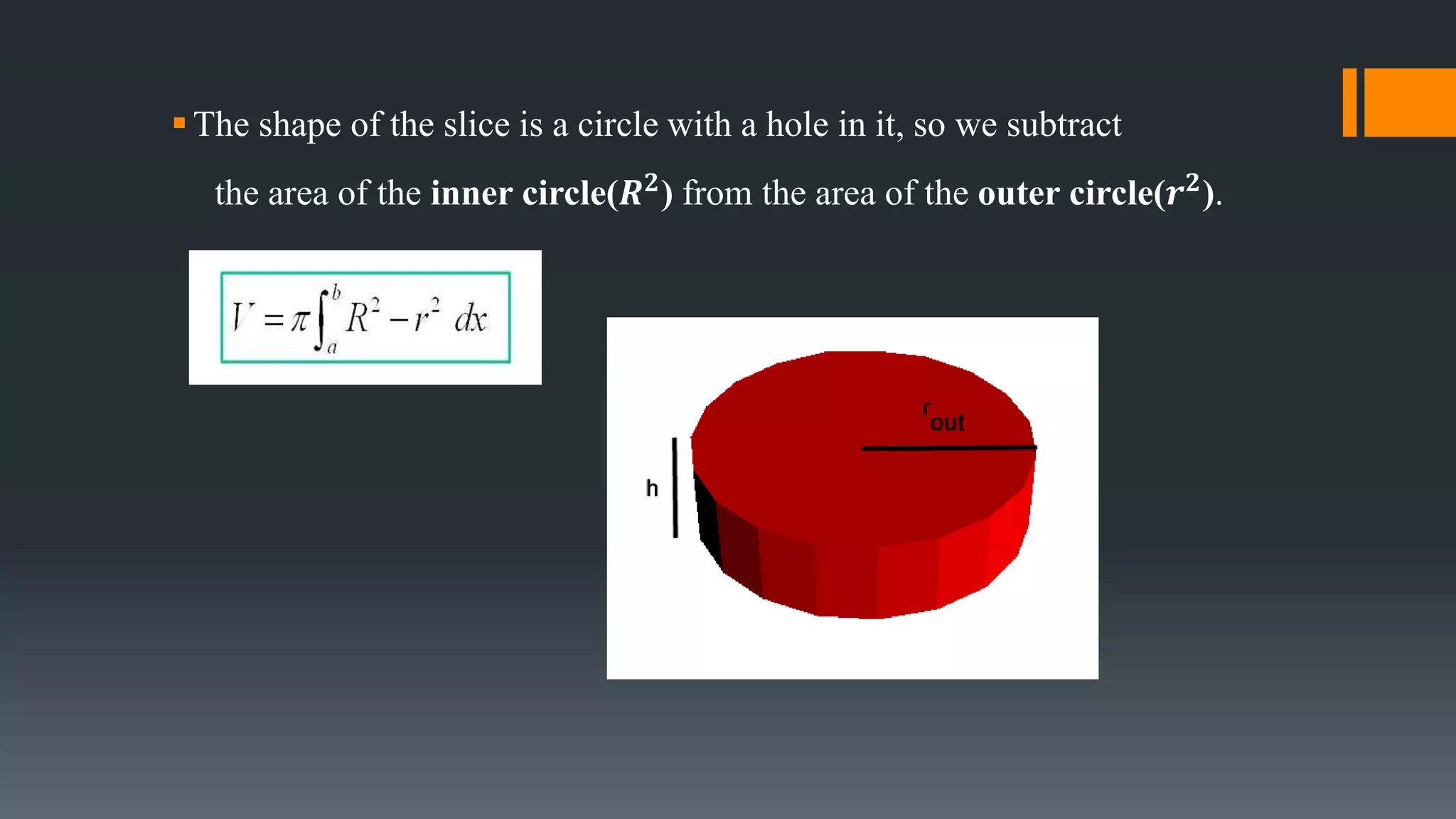
The document discusses different methods for calculating the volume of a solid of revolution: disk method, washer method, and shell method. It provides examples of applying each method to find the volume generated when an area bounded by curves is revolved around an axis. The disk method calculates volume by summing the volumes of thin circular disks. The washer method accounts for holes by subtracting the inner circular area from the outer. The shell method imagines the solid as nested cylindrical shells and sums their individual volumes.

2. Volume of solid revolution
Submitted to:
 Mam Mehwish
Submitted by:
 Beenish Ebad
 Amna javed
Course :
 BS.Ed -3

3. Volume of solid of revolution:
“A solid of revolution is a three-dimensional object
obtained by rotating a function in the plane about a line
in the plane. The volume of this solid may be calculated
by means of integration.’’

4. Real life use of volume of solid revolution:
Engineering, medical imaging, and geometry.
 The manufacturing of machine parts and the creation
of MRI images both require understanding of these
solids.

5. Common methods for finding the volume are:
Disc methods
Washer method
Shell method

6.  The disk method, also known as the method of disks or rings, is a way to calculate the
volume of a solid of revolution by taking the sum of cross-sectional areas of infinitesimal
thickness of the solid.
 To find the volume of solid of revolution by disc method is,
V = 𝒂
𝒃
𝝅 𝒇 𝒙 𝟐
𝒅𝒙

7. Example :
The area in the first quadrant bounded by the parabola the area in the first quadrant
bounded by the parabola y2=4ax and its latus –rectum is revolved about the x-axis.
Find the volume of the solid generated.
Solution:
𝑦2
= 4𝑎𝑥
V = 0
b
π y2
dx
= 4ax 0
a
xdx
= 2πa3
O
x
y
x=a

8. find the volume generated by revolving the
area in the first quadrant bounded by the
𝑦2
= 8𝑥 and its latus-rectum about the x-axis.
 Solution :
 Given equation of parabola is,
 𝑦2
=8x
 And e.q of latus rectum is
 x = 2
 Let v be the required volume then.
 V = π 0
2
y2
dx
 V = π 0
2
8𝑥dx
 =8𝜋
𝑥2
2 0
2
 = 4𝜋 (2)2
−(0)0
 = 4𝜋 4 − 0
 = 16𝜋 𝑐𝑢𝑏𝑖𝑐 𝑢𝑛𝑖𝑡
Y-axis
X-axis
S(2,0)
o

9. Washer method:
The application of method of slicing a cone is called the washer method.
A washer is like a disk but with a center hole cut out.

10. The shape of the slice is a circle with a hole in it, so we subtract
the area of the inner circle(𝑹 𝟐) from the area of the outer circle(𝒓 𝟐).

11. We’ll need to know the volume formula for a single washer.
V = π (r2
2 – r1
2) h = π (f(x)2 – g(x)2) dx.
As before, the exact volume formula arises from taking the limit as
the number of slices becomes infinite.

12.  Washer along x-axis: Washer along y-axis:

14. Example:
 Solve question by using washer method.
𝑦 = x, y = 1, x = 0.
Solution:
Given equation are 𝑦 = 𝑥, … … . 1 , 𝑦 = 1 … … (2)
To find the point of intersection compare eq(1) and (2)
𝑥 = 1 and we know 𝑥 = 0.
outer radius = R(x) = 1, inner radius = r(x) = x
V = 𝑎
𝑏
𝜋 𝑅2
− 𝑟2
𝑑𝑥
= 𝜋 0
1
1 − 𝑥2
𝑑𝑥
= 𝜋 𝑥 −
𝑥3
3
1
0
= 𝜋[(0 −
0
3
) − (1 −
1
3
)]
=
2
3
𝜋 ANS.

15. Example: Determine the volume of the solid. Here, the bounding curves for the generating
region are outlined in red. The top curve is y = x and the bottom one is y = x2
SOLUTION:
Given equation are 𝑦 = 𝑥, … … . 1 , 𝑦 = 𝑥2 … … (2)
To find the point of intersection compare eq(1) and (2)
𝑥 = 𝑥2 ⇒ 𝑥 − 𝑥2=0 ⇒ 𝑥 1 − 𝑥 = 0
𝑥 = 0 𝑎𝑛𝑑 𝑥 = 1
outer radius = R(x)= b = 𝑥2
, inner radius = r(x)= a = x

16. Shell method:
Introduction:
Suppose you need to find the volume of a solid of revolution. First we
have to decide how to slice the solid. If you wanted to slice perpendicular to
the axis of revolution, then you would get slabs that look like thin cylinders
(disks) or cylinders with circles removed (washers). However, the Shell
Method requires a different kind of slicing.

17. Imagine that your solid is made of cookie dough. And you have a set of
circular cookie cutters of various sizes. Starting with the smallest cookie
cutter and progressing to larger ones, let’s slice through the dough in
concentric rings.
Making sure to slice in the same direction as the axis of revolution, you
will get a clump of nested shells, or thin hollow cylindrical objects.

18. Now let’s take a closer look at a single shell.
Cylindrical shell with height h, radius r, and thickness w.
As long as the thickness is small enough, the volume of the shell can
be approximated by the formula:
V = 2πrhw

19. we have the following info about each shell:
 Its radius is r = x (distance from a typical point to the y-axis).
 The height is h = y = f(x).
 Its thickness is a small change in x, which we label as Δx or dx.
Therefore, the approximate volume of a typical shell is:
V = 2πx × f(x) × dx

20. Integration:

21. EXAMPLE: Find the volume of the solid generated by revolving the region under f(x) = x2 + 1,
where 2 ≤ x ≤ 6, around the y-axis.
Solution:
First identify the dimensions of a typical shell.
r = x
h = f(x) = x2 + 1
Thickness = dx
In addition, we use a = 2 and b = 6 because we have 2 ≤ x ≤ 6. Now set up the Shell Method integral and
evaluate to find the volume.