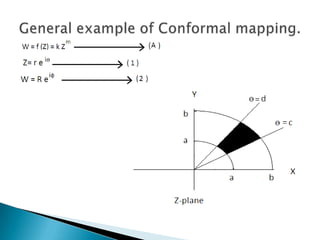
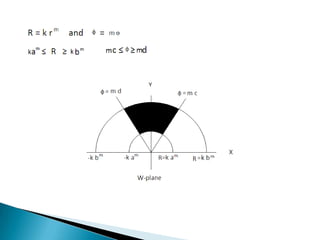
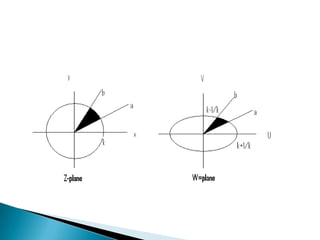
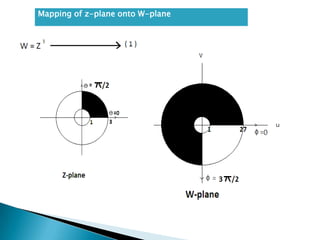
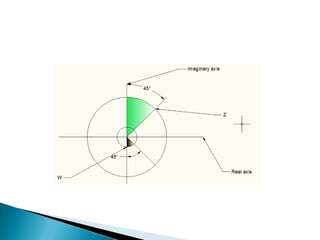
The document discusses the history and uses of mapping and conformal mapping. It provides examples of some of the oldest known maps dating back to 6200 BC. It then discusses how conformal mapping originated from rejecting the idea that the Earth is flat, and how conformal mapping preserves angles to give a realistic view of the physical world on a map. Some key uses of conformal mapping mentioned are finding inverses of complex numbers, solving Laplace equations, and determining heat conduction.

1. Name ID
JamAbdulSattar k11-2251 (c)
Sadiq Shah K11-2395 (c)
Nazim Khan K11-2410 (c)
Akhtar Afzal k11-2441 (A)
Muhammad Ishtiaq K11-2442 (c)

3.  Mapping:
To give realistic view to the physical
world.
 Conformal Mapping:
Advanced method of forming maps
preserving angles and to give the realistic view to
the image or map.

4.  According to many historians,
“Mapping is older than “the written word “.
 Mapping is used to give life to the physical world
on a piece of paper.
 And to prove this statement that mapping is very
old science, a lot of examples are present in the
history.

5.  A map of planned town is found on the wall of 9ft
in Ankara, Turkey which is 6200 B.C old.
 A map of South Africa is found which was made by
the Chinese Great Ming Empire in 1389.
 Different maps of the world were drawn by
different travelers to help others in sea journey.

6.  All these mappings were done to help improving
the life style and travelling.
 But at old times there were also the quest of
improving different sciences.
 In 1999, the oldest known map of the moon is
discovered in Ireland, which is 3000 B.C old.

7.  There are different drawings found in France which
are about “Summer triangle” changes in weather
and are 14000 B.C old.

8.  The history of Conformal mapping is traced back to
16th century.
 G-Mercator was the mathematician who
contributed the first in conformal mapping.
Origination:
 Its origination was from the rejection of idea that
earth is flat.

9.  Firstly it was thought that earth is flat but this idea
was rejected because there is no Isometry (distance
preserving),as one position and travelled distance
can’t be exactly shown, it was the origination of
Conformal mapping which supports the idea that
earth is sphere by preserving angles.

10.  Theorem
If f: A → B is analytic and f '(z) ≠ 0 for all z in A,
then f is conformal.
“If a function is harmonic over a particular space
where it satisfies certain boundary conditions, and
it is transformed via a conformal map to another
space, the transformation is also harmonic and
satisfies corresponding boundary conditions”.
uxx + uyy = 0 ( Laplace equation)
 It is a geometric approach to a complex analysis.
 Applicable at all the points where function is
analytic except the critical points.

11.  In conformal mapping we define another plane W
which is also a complex plane and then convert Z-
plane to W-plane to get conformal map.

15. Mapping of z-plane onto W-plane

16.  Failure of conformality points
 W = Sin
 To find the points at which the conformality
fails, we take derivative and then find the critical
points which are the points of failure of
conformality
 So taking derivative on both sides
 dw = d/dz(Sin )
 dw= cos -----(1)

 for finding the critical points we get
 dw= 0
 put it in eq (1)
 cos = 0
 So Z= 1/2 , 3/2,5/2 , 7/2,……
 Z=(2n-1)/2 where n E N

17. We can find the inverse of complex number by
using Conformal Mapping.
Procedure:
.Let Z=2 as in general here π/4<α<π/2
Also r=2
Required: W=1/Z ?
Solution:
β is the angle of conformal mapping,
and R Is the radius of the circle in which we draw conformal
map.
putting the value of Z in equation which is to be determined.
we get

18.  W=1/(2eiα) , W=0.5e-iα (1) π/4< α< π/2
also
by comparing equation (1) and (2) we get
R=0.5, β=-α to find limit of β putting value of α
if α=π/4 β=-π/4
if α=π/2 β=-π/2 thus -π/4<β<-π/2
thus we can easily determine inverse of Z by using conformal
map.

20. (1)We can find the inverse of complex number with the help of conformal
mapping.
(2)Integration can also be determined by conformal mapping.
(3)Laplace equations can also be solved with the help of conformal
mapping.
(4)We can also determine the conduction of heat by it.
(5)Conformal mapping has also advantages in fluid dynamics.