The document discusses the concept of double integrals, particularly over rectangular regions, and their applications in calculating volumes. It provides definitions, properties, examples, and theorems related to double integrals and iterated integrals. Additionally, the document touches upon integration in polar coordinates and presents exercises for evaluation.

1. Multiple Integral

2. Double Integrals over Rectangles
Remark ：
)(point.sample
acalledisx1,2,...n,i],x,[xxChoose4.
Pofnorm}Thex,,x,xmax{|P|3.
n,1,2,i,x-xxDefine2.
b],[aofpartitionacalledisPThen
bxxxaand}x,,x,{xPLet1.
ii1-ii
n21
1-iii
n10n10
取樣點
=∈
∆∆∆=
==∆
=<<<==




3. ∑∫ =
→
=∆=
n
1i
ii
b
a 0P||
SofareaThex)xf(limf(x)dx
b],[aonfofintegraldefiniteThe5.
f(x)}y0b,xa|y){(x,S ≤≤≤≤=

4. [2,3][1,2]2.
4}y21,x0|Ry){(x,[2,4][0,1]1.
Rectangle:Example
d}ycb,xa|Ry){(x,d][c,b][a,R
RrectangleclosedA6.
2
2
×
≤≤≤≤∈=×
≤≤≤≤∈=×=

5. Double Integrals and Volumes
V(S)-SofvolumethefindTo
y)}f(x,zR,0y)(x,|Rz)y,{(x,Sd],[c,b][a,RLet 3
≤≤∈∈=×=
lssubintervaintoRrectangletheDivide
f(x)dxdefinetoSimilarly
b
a∫

6. ∑∑
∑∑
= =
= =
∆≈
∆
∆∆=∆
==×=
==∆
=∆=
n
1j
m
1i
ij
*
ij
*
ij
n
1j
m
1i
ij
*
ij
*
ij
ij
*
ij
*
ij
jiijij
j1-ji1-iij
1-jjjj1-j
1-iii
i1-i
A)y,f(xV(S)i.e
A)y,f(xeapproximatcanSofvolumeThe
Reachin)y,(xpointsampleachoose
yxAisRofareaThe
n1,j;m1,i]y,[y]x,[xRDefine
n1,2,j,y-yy],y,[ylsubintervaninto
dividedisd][c,and,x-xxm,1,2,i
]x,[xlsubintervamintodividedisb][a,




7. n1,2j;m1,2i,R
diagonallongesttheoflengththedenote|P|Let
ij  ==

8. ∑∑∫∫
∫∫
= =
→
∆=
m
1i
n
1j
ij
*
ij
*
ij
0P||
R
R
A)y,f(xlimy)dAf(x,
y)dAf(x,isRrectangleover thefofintegraldoubleThe
:Definition

9. ∫∫ ∫∫
∫∫ ∫∫ ∫∫
∫∫ ∫∫
≥
∈∀≥
+=+
=
R R
R R R
R R
y)dAg(x,y)dAf(x,
thenR,y)(x,y)g(x,y)f(x,If3.
y)dAg(x,y)dAf(x,y))dAg(x,y)(f(x,2.
y)dAf(x,cy)dAcf(x,1.
:properties
existslimitthisif

10. Ronintegrableisfthencurves,smooth
ofnumberfiniteaonexceptRoncontinuousisfIf(ii)
RonintegrableisfthenR,oncontinuousisfIf(i)
Rrectabgleclosedon theboundedbefLet
1Theorem
Roverfofintegraldoublethecalledisy)dAf(x,2.
existA)y,f(xlimifR,onintegrableisf1.
:Definition
R
m
1i
n
1j
ij
*
ij
*
ij
0P||
∫∫
∑∑= =
→
∆

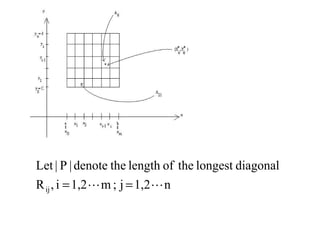
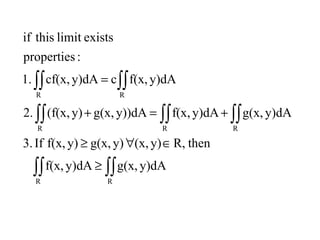
11. ww),(o,oncontinuousnotisf
(0,1)oncontinuousnotisf
0x0,
0x,
x
y
y)f(x,3.
Roncontinuousisf
)[0,)[0,Rx,yxy)f(x,2.
Roncontinuousisf
][0,2][0,Ry)(x,sinxy,y)f(x,1.
:Example
RoncontinuousisfthenR,b)(a,allatcontinuousisfIf2.
b)(a,atcontinuousisfthenb),f(a,y)f(x,limIf1.
:Definition
2
b)(a,y)(x,
∀




=
≠
=
∞×∞=+=
×=∈=
∈
=
→
ππ

12. Iterated Integrals
integraliteratedancalledis)dxy)dyf(x,(A(x)dx
y)dxf(x,B(y)y)dy,f(x,A(x)Let1.
d][c,b][a,Ry),f(x,functionFor
:Remark
)dyydxx(A(y)dyConsider
y
3
26
1
3
3
x
yydxxA(y)Lety,Fixed
b
a
d
c
b
a
d
c
b
a
2
0
3
1
2
2
0
3
3
1
2
∫ ∫∫
∫ ∫
∫ ∫∫
∫
=
==
×=
=
=⋅==

13. ∫ ∫
∫ ∫
∫ ∫
∫ ∫∫ ∫
∫ ∫∫ ∫
∫ ∫∫ ∫
+
+
+
=
=
3
0
2
1
8
0
4
0
2
4
0
8
0
2
3
0
4
1
2
3
0
4
1
2
d
c
b
a
d
c
b
a
b
a
d
c
b
a
d
c
2y)dxdy(3x(v)
)dxdyy8x-(64
4
1
(iv)
)dydxy8x-(64
4
1
(iii)
ydydxx(ii)ydxdyx(i)
evaluate:Example
)dxy)dyf(x,(y)dydxf(x,3.
)dxy)dyf(x,(y)dydxf(x,2.

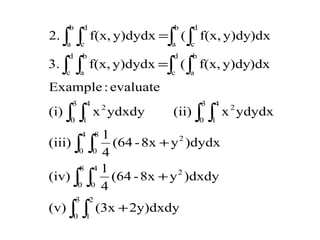
14. 1}y02,x-1|y){(x,Rwhere,dA
x1
y1
Find4.
][0,][0,Rwhere,xcosxydAFind3.
0-)
0
sin2y
2
1
(-
cos2y)dy-(1dy
0
2
(-cosxy)ysinxydxdyBut
?ysinxydydxysinxydA:Ans
][0,[0,2]Rwhere,ysinxydAFind2.
[1,3][0,2]RwheredA,)3y-(xFind1.
:Ex
y)dydxf(x,y)dxdyf(x,y)dAf(x,
thed],[c,b][a,RoncontinuousisfIf
Theorem)s(Fubini'2Theorem
R
R
000
2
0
2
0 0
R
R
R
2
b
a
d
c
d
c
b
a
R
≤≤≤≤=
+
+
×=
===
==
==
×=
×=
==
×=
∫∫
∫∫
∫∫∫ ∫
∫ ∫∫∫
∫∫
∫∫
∫ ∫∫ ∫∫∫
ππ
ππ
π
π
π
πππ
π

15. { }
1y)dAsin(xD
thatshow[0,1],[0,1]RIf2.
2y14,x34,
2y13,x11,
1y04,x12,
y)f(x,2.
2y04,x33,
2y03,x12,
y)f(x,1.
functiongiventheisfwherey)dA,f(x,
Evaluate,2y03,x1|y)(x,RLet1.
Exercises
R
R
≤+≤
×=





≤≤≤≤
≤≤<≤
≤≤≤≤
=



≤≤≤<
≤≤≤≤
=
≤≤≤≤=
∫∫
∫∫

16. ∫∫
∫∫
∫∫
∫∫
∫∫ ∫∫ ∫∫
+
+
===
≤≤≤≤=
×=≤≤≤≤=
R
R
R
R
R R R
2
1
y))dA4g(x,y)(3f(x,4.
4)dAy)(2f(x,3.
y)dA3g(x,2.
y))dAg(x,-y)(4f(x,1.
Evaluate
2y)dAg(x,6,y)dAg(x,4,y)dAf(x,thatSuppose
2}y12,x0|y){(x,R
[0,2][0,2]R1},y02,x0|y){(x,RLet3.
1
2

17. ∫ ∫
∫ ∫
∫ ∫
∫ ∫
∫ ∫
∫ ∫
∫ ∫
+
=
2
2-
1
1-
2
2-
3
1
1-
2
2
2-
1
1-
32
2
0
2
0 2
0
1
0
1
0
1
0
xy
2
0
3
1
2
dydx|y|[x](vii)
dydxy][x(vi)
dydx|yx|(v)
dydx
x1
y
(iv)
xsinydxdy(iii)
dxdyxe(ii)
yxy)f(x,wherey)dydx,f(x,(i)
integralsinteratedtheofeachEvaluate4.
π

18. { }
2}y,13x0|y){(x,R,dAx1xy(v)
[0,1][0,1]R,dAxye(iv)
1}y02,x-1|y){(x,RdA,
y2
x1
(iii)
]
3
[0,]
6
[0,Ry)dA,xcos(x(ii)
3y02,x1y)(x,R)dA,3xy-(2y(i)
integraldoubletheCalculate5.
R
2
R
yx
R
R
R
32
22
≤≤≤≤=+
×=
≤≤≤≤=
+
+
×=+
≤≤≤≤=
∫∫
∫∫
∫∫
∫∫
∫∫
ππ

19. ∫ ∫ ∫∫
∫ ∫∫ ∫
∫ ∫ ∫∫
+
≤≤≤≤
++=
+
1
0
4
0
3
2x
y
y
0
x
1
0
1
y
3
1
0
3
3y
x
1
0
1
0
x2
x-1
2
x
0
2
dydxe(vi)dxdy2ye(v)
dxdyx1(iv)dxdye(iii)
)dydxy-(3x(ii)dydxcosx(i)
integralinteratedtheEvaluate7.
4)y10,x(-1|y){(x,
rectangletheaboveand15y2xZ
planeunder thelyingsolidtheofvolumetheFind6.
2
2
2

20. 1zyxand
0z0,y0,xplanesby theBounded(ii)
2zy
and2yxcylindersby theBounded(i)
solidgiventheofvolumetheFind9.
1}yx|y){(x,DwheredA,y-x-1Evaluate8.
222
222
22
D
22
=++
===
=+
=+
≤+=∫∫

21. 

 ∈
=
DinnotbutRinisy)(x,if0
Dy)(x,ify)f(x,
y)F(x,
Double Integral over General Regions
functionnewaDefineD.on
definedfunctionaisfR,DandregionboundedabeDLet ⊂

22. function.continuoustwoareh,hwhere
d},yc(y),hx(y)h|y){(x,D
ifIItypeofbetosaidisDregionplaneA3.
function.continuoustwoareg,gwhere
(x)},gy(x)gb,xa|y){(x,D
ifItypeofbetosaidisDregionplaneA2.
y)dAF(x,y)dAf(x,
isDoverfofintegraldoubleThe1.
:Definition
21
21
21
21
D R
≤≤≤≤=
≤≤≤≤=
=∫∫ ∫∫

23. d}yc(y),hx(y)h|y){(x,Dwhere
y)dxdyf(x,y)dAf(x,
thenDregionIItypeaoncontinuousisfIf2.
y)dydxf(x,y)dAf(x,then
(x)},gy(x)gb,xa|y){(x,D
such thatDregionItypeaoncontinuousisfIf1.
:Properties
IIType},y1x2y1,y-1|y){(x,D2.
IType1},ysinx,x0|y){(x,D1.
:Example
21
D
d
c
(y)h
h
D
b
a
(x)g
g
21
22
2
1
2
1(y)
2
1(x)
≤≤≤≤=
=
=
≤≤≤≤=
+≤≤≤≤=
≤≤≤≤=
∫∫ ∫ ∫
∫∫ ∫ ∫
π

24. 2
2
1
-1
2
3
1-
1
)x
2
1
-xx
2
3
x
4
1
-x
2
1
(
dx4x-x
2
3
3x
2
3
2x-xx
)dx)(2x-)x((1
2
3
)2x-xx(1
3y)dydx(x3y)dA(x
:Ans
}x1y2x1,x-1|y){(x,DWhere
3y)dA(xEvaluate1.
:Example
5342
1
1-
44233
1
1-
222222
D
1
1-
x1
2x
22
D
2
2
=+=++=
++++=
+++=
+=+
+≤≤≤≤=
+
∫
∫
∫∫ ∫ ∫
∫∫
+

25. 62xyparabolatheand1-xylinethe
byboundedregiontheisDxydA whereEvaluate2.
2
D
+==
∫∫
36xydxdyxydA
4}y2-1,yx
2
6-y
|y){(x,
}62xy?5,x-3|y){(x,D
:Sol
D
4
2-
1y
2
6-y
2
2 ==
≤≤+≤≤=
+≤≤≤≤=
∫∫ ∫ ∫
+

26. :Sol
2z2yxand0z0,x2y,x
planesby theboundedontetrahedrtheofvolumetheFind3.
=++===
3
1
2y)dydx-x-(22ydA-x-2V
}
2
x-2
y
2
x
1,x0|y){(x,D
D
1
0
2
x-2
2
x
=
==
≤≤≤≤=
∫∫ ∫ ∫所求

27. y}x01,y0|y){(x,
1}yx1,x0|y){(x,D
:Sol
)dydxcos(yEvaluate5.
cos1)-(1
2
1
;)dydxsin(yEvaluate4.
1
0
1
x
2
1
0
1
x
2
≤≤≤≤=
≤≤≤≤=
∫ ∫
∫ ∫

28. Double Integrals in Polar Coordinates
βθαθ ≤≤≤≤= b,ra|){(r,RConsider
Polar rectangle

29. Example ：
3
2
)
3
-
2
()1-(3
2
1
2
3
-
2)1-3(A(R)isRofareaThe
}
23
3,r1|){(r,R3.
}03,r1|){(r,R2.
}201,r0|){(r,R1.
22
22
π
ππ
π
ππ
ππ
π
θ
π
θ
πθθ
πθθ
=
⋅=
⋅⋅=
≤≤≤≤=
≤≤≤≤=
≤≤≤≤=

30. n1,jm;1,i-,r-rrWhere
rr
)r-)(rr(r
2
1
r
2
1
-r
2
1
A
isA-RofareaThe
},rrr|){(r,R4.
1,-jjj1-iii
ji
*
i
j1-ii1-iij
2
1-ij
2
iij
ijij
j1-ji1-iij
 ===∆=∆
∆∆=
∆+=∆∆=∆
∆
≤≤≤≤=
θθθ
θ
θθθ
θθθθ
∫ ∫
∑∑
∑∑
→
∆∆=
∆
= =
= =
β
α
θθθ
θθθ
θθ
b
a
m
1i
n
1j
ji
*
i
*
j
*
i
*
j
*
i
m
1i
n
1j
ij
*
j
*
i
*
j
*
i
)rdrdrsin,f(rcos
r)rsinr,cosf(r
A)sinr,cosf(r
isRonfofsumRiemanuThe

31. ∫∫ ∫ ∫
∫∫ ∫ ∫
=
≤≤≤≤=
=
≤≤
≤≤≤≤=
D
)(h
)(h
21
R
b
a
2
1
)rdrdrsin,f(rcosy)dAf(x,
thenDoncontinuousisfIfregion.
polorabe)}(hr)(h,|){(r,DLet2.
)rdrdrsin,f(rcosy)dAf(x,
thenR,oncontinuousisfIf2-0andrectangle
polarabe}b,ra|){(r,RLet1.
Properties
β
α
θ
θ
β
α
θθθ
θθβθαθ
θθθ
παβ
βθαθ

32. π
θθθ
θθθ
πθθ
π
π
2
15
)d7cos(15sin
)rdrd3rcos)(4(rsin3x)dA(4y
}02,r1|){(r,
4}yx10,y|y){(x,R
:Sol
4}yx10,y|y){(x,Rerewh
3x)dA(4yEvaluate1.
:Example
0
2
R
0
2
1
22
22
22
R
2
=
+=
+=+
≤≤≤≤=
≤+≤≥=
≤+≤≥=
+
∫
∫∫ ∫ ∫
∫∫

33. 2
)rdrdr-(1
)dAy-x-(1V
}201,r0|){(r,D
:Sol
y-x-1zparaboloidtheand
0zplaneby theboundedsolidtheofvolumetheFind2.
2
0
1
0
2
D
22
22
π
θ
πθθ
π
=
=
=
≤≤≤≤=
=
=
∫ ∫
∫∫

34. π
θθ
πθθ
π π
)de
2
1
-
2
1
(limdrdrelim
dAelimdAe
}20n,r0|){(r,DConsider
:Sol
}y-,x-|y){(x,Rewher
dAeEvaluate
:Example
2
0
2
0
n-
n
n
0
r-
n
D
)y(x-
n
R
)y(x-
n
2
R
)y(x-
22
n
22
2
22
2
22
=
==
=
≤≤≤≤=
∞<<∞∞<<∞=
∫ ∫∫
∫∫∫∫
∫∫
∞→∞→
+
∞→
+
+

35. The Cross Product
nofdirectionin thepointsyour thumbthen,btoafromanglethe
throughcurlhandrightyouroffingerstheIf:rulehand-rightby the
givenisdirectionwhoseandbandabothlar toperpendicutorvec
unitaisnand,0,bandabetweenangletheisrewhe
n)sin|b||a(|bavectortheisbandaofproductcrossThe2.
cos|b||a|baisbandaofproductinnerThe1.
vectorsldimensionathreenonzerotwobeba,Let
θ
πθθ
θ
θ
≤≤
=×
=⋅
Definition

36. Example ：
a
θ
bn
.1 .2
a
b
n
ab-ba3.
-jkij,ik(iii)
-ijki,kj(ii)
-kijk,ji(i)
(0,0,1)k(0,1,0),j(1,0,0),i2.
0baifonlyandifparallelarebanda1.
Properties
×=×
=×=×
=×=×
=×=×
===
=×

37. k
bb
aa
j
bb
aa
-i
bb
aa
bbb
aaa
kji
)ba-ba,ba-ba,ba-b(aba
then),b,b,(bb),a,a,(aaIf5.
DbDaD)ba((iii)
Daba)Db(a(ii)
)b(ca)bac(b)a(c(i)
scalarabeacLet4.
21
21
31
31
32
32
321
321
122131132332
321321
3
+==
=×
==
×+×=×+
×+×=+×
×=×=×
.6
a
b
θ
R b |ba|A(R)
isRofareaThe
×=

38. kj-iandjibothtoorthogonalrsunit vectotwoFind4.
baFindk,-jibk,jia3.
k13j-43iba
(2,7,-5)b(1,3,4),a2.
5k3j-6i
021
31-2
kji
ab
5k-3j-6i
31-2
021
kji
ba
(2,-1,3)b(1,2,0),a1.
Example
++
×+=++=
++=×
==
++==×
==×
==

39. Ssurfaceparametricacalledis
RDv)(u,,
v)z(u,z
v)y(u,y
v)x(u,x
such that
Rz)y,(x,pointsallofsetThe2.
t,
y(t)y
x(t)x
:curveparametric1.
:Definition
2
3





⊂∈
=
=
=
∈



≤≤
=
=
βα
Surface Area

40. Rvv,y4,zxhaveweS,z)y,(x,anyFor
surfaceparametricaisS
2sinu}zv,y2cosu,x|z)y,{(x,S1.
:Example
22
∈==+∈
====
x
z
y
)2,0,0(

41. 0)r-(rnplanetheofequationA vector
planetheofvectornormalaisn
z)y,(x,rwhere0)r-(rnbydenotedisplaneThe4.
vectornormalacalledisnvectororthogonalThis
plane.thetoorthogonalisnvectoraandplanethe
in)z,y,(xPrpointabydeterminedisspaceinplaneA3.
:Definition
0
0
00000
=⋅
==⋅
=
x
z
y
r
0r
),,( zyx
n
),,( 00000 zyxpr =

42. 02)-14(z3)-20(y1)-12(x:Sol
R(5,2,0)Q(3,-1,6),P(1,3,2),
pointshethrough tpassesthatplanetheofequationanFind
:Example
(1,2,3)n6},3z2yx|z)y,{(x,S3.
(2,-4,1)n0},z4y-2x|z)y,{(x,S2.
0}4)-z1,y3,-(x(1,2,4)|z)y,{(x,S1.
:Example
=++
==++=
==+=
=+⋅=

43. 
72)
42
2
(cos,
42
2
nn
nn
cos
planesebetween thanglethebeLet
(1,-2,3)n(1,1,1),nareplanestheseofvectorsnormalThe
:Sol
23z2y-xand1zyxplaneebetween thangletheFind
:Example
anglethehavetorsvec
normaltheirifisSandSplanesebetween thangleThe6.
parallelarevectorsnormaltheirifparallelareplaneTwo5.
:Definition
1-
21
21
21
21
≈==
⋅
=
==
=+=++
θθ
θ
θ
θ

44. 9
y
y)f(3,
2x,
x
f(x,1)
y,xy)f(x,z
:Example
2
=
∂
∂
=
∂
∂
==
1L
2L
)1,(:1 xfzC =
),3(:2 yfzC =
x
y
z
ii Coflinetangenttheis1,2,i,L =

45. 0rrifsmoothcalledisSsurfaceThe(v)
k
u
)v,z(u
j
u
)v,y(u
i
u
)v,x(u
r
isectortangent vThecoSimlarly t(iv)
k
v
)v,z(u
j
v
)v,y(u
i
v
)v,x(u
r
obtainedis)v,z(uz),v,y(uy
)v,x(uxwhere)z,y,(x-Patcector totangent vThe(iii)
Sonlyingccurvegrida
definesanduparametersingletheoffunctionvectorais)vr(u,(ii)
Sonlyingccurvegrida
definesandvparametersingletheoffunctionvectoraisv),r(ui)(
)v,(uFixedv)kz(u,v)jy(u,v)ix(u,v)r(u,
v)}x(u,xv),y(u,yv),z(u,z|z)y,{(x,S
bydefinedbeandsurfaceparametricabeSLet
:Definition
vu
000000
u
2
000000
v
000000
00000001
2
0
1
0
00
≠×
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
+
∂
∂
=
==
=
++=
====

46. Exercises 2
pageofoutofpage
theintodirectedisuwhether vdetermineand|vu|Find2.
(0,2,4)b(1,2,0),a(iii)
(5,-2,-1)b(1,2,-3),a(ii)
(3,0,1)b(-2,3,4),a(i)
ab,baproductcrosstheFind1.
××
==
==
==
××
5|| =u
6|| =u
6|| =u
)2,0,1(=u
5|| =v
8|| =v
)2,1,1(=v
8|| =v

60 
60

150

47. y)f(x,limFind(ii)
(0,0)atcontinuousnotisy)f(x,thatshow(i)
(0,0)y)(x,if,1
(0,0)y)(x,if,
yx
xy
y)f(x,
functionheConsider t4.
not?or whywhy(0,0)?atcontinuousfIs
(0,0)y)(x,if,0
(0,0)y)(x,if,
yx
yx
y)f(x,
functionheConsider t3.
o)(o,y)(x,
22
24
2
→




=
≠
+=




=
≠
+=

48. followingin theregiontheisDwhere,xydAEvaluate5.
D
∫∫
D
x
y
2
xy =
2
1
y =
2yx =+
∫∫ ≤+≤=
D
222
4}yx1|y){(x,Dwhere)dA,sin(xyEvaluate6.

49. ∫∫
∫∫
=+=+
D
2
2222
D
2
dAxyEvaluate8.
4yxcircletheand42yx
ellipseebetween thregiontheisDwheredA,xEvaluate7.
D
2
4
(2,4)
∫ ∫ ∫ ∫
∫ ∫∫ ∫
π θ π
π θπ θ
θ
θθθθ
0
Sin
0 0
Siny
0
22
0
Cos-1
0
2
0
Cos
0
2
dxdyx(iv)drdr(iii)
drdrSin(ii)drdSinr(i)
integralsiteratedtheEvaluate9.

50. { }
∫ ∫
∫∫∫∫
∫ ∫
∫ ∫
∫∫
≤+=
++
+
+
=+
+
3
4
4
3
5Sec-
0
23
222
D
22
D
22
2
1
x-2x
0
2
1
-
22
1
0
y-1
0
22
22
D
yx
drdSinr
evaluatethenandscoordinaterrectangulaSwitch to12.
4yx|y)(x,D
wheredA,|yxSin|,yxSin(iii)
dydx)y(x(ii)
)dxdyySin(x(i)
Evaluate11.
4yx
byenclosedregiontheisDwhere,dAeEvaluate10.
2
2
22
π
π
θ
θθ
π

51. ∫ ∫ ∫ ∫ ∫ ∫
∫ ∫ ∫∫ ∫ ∫
+
≤≤=
≤≤=
≤+=+==
=+=
3
0
x-9
0
x
0
1
0
2x
x
yx
0
0
2
0
z-4
0
1
0
z
0
y
0
3
22
22
2
2
2xydzdydx(iv)yzdydzdx(iii)
yzsinydxdzd(ii)xyzdxdydz(i)
integraliteratedtheEvaluate16.
9x4,xy(ii)
2x0,xy(i)
axis-xabout the
curvegiventherotatingbyobtainedsurfacetheofareatheFind15.
1vuv,-uzv,uyuv,xsurfacetheofareatheFind14.
9zplanethebelowyxzsurfacetheofareatheFind13.
π

52. ),,(coordinateSpherical1.
:Example
k
v
z
j
v
y
i
v
x
rk
u
z
j
u
y
i
u
x
rwhere
dA|rr|A(S)isSofareasurfacethen theD,domain
parametert thethroughourangesv)(u,asoncejustcoveredisSand
Dv)(u,v)k,z(u,v)jy(u,v)ix(u,v)r(u,
equationby thegivenisandsurfaceparametricsmoothabeSLet1.
Definition
vu
D
vu
φθρ
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
+
∂
∂
=
×=
∈++=
∫∫
x
y
z
0
φ
θ
φ ),,p(
z)y,p(x,
φθρ
cosz
00,sinsiny
cossinx
zyx|op|where 222
φρ
πφρθφρ
θφρ
ρ
=
≤≤≥=
=
++==

53. 4
,cos
4
2sin1cossinx
4
,2cos2cosz
2)2(11zyx(i)
:Sol
,-2)3(0,2(iii),0,1)3((ii))2(1,1,(i)
scoordinatesphericalr torectangulafromChange3.
2
1
3
cos1z
4
6
4
sin
3
sin1y
4
6
4
cos
3
sin1x)
3
,
4
(1,
coordinateSphericalscoordinaterrectangulatheFind.2
222222
π
θθ
π
θφρ
π
φφφρ
ρ
π
ππ
ππππ
==⇒=
==⇒=
=++=++=
=⋅=
=⋅=
=⋅=

54. ksin16cosjsin16sin-icos-16sin
4sin-sin4coscos4cos
0cos4sinsin4sin-
kji
rr
k)4(-sinjsin4cosicos4cosr
k0jcos4sinisin-4sinrcaculate
}0,20|),{(D),(and
k4cosjsin4sinicos4sin),r(
isequationparametricThe:Sol
SofareasurfacetheFind(ii)
4radiusofsphericalaofsurfaceThe-S
20,0
4cosz,sin4siny,cos4sinx|z)y,(x,
S(i)
Ssurfaceparametric.4
22
φφθφθφ
φθφθφ
θφθφ
φθφθφ
θφθφ
πφπθφθφθ
φθφθφφθ
πθπφ
φθφθφ
φθ
φ
θ
+=
=×
⋅+⋅+⋅=
⋅+⋅+⋅=
≤≤≤≤=∈
⋅+⋅+⋅=






≤≤≤≤
===
=

55. ∫∫
∫∫ ∫ ∫
×=
⋅==×=
=
++=×
D
vu
D
0
2
0
22222
dA|rr|A(S)1.
Remark
164dd16sindA|rr|A(S)
16sin
)sin(16cos)sin(-16sin)cos(-16sin|rr|
Thus
π π
φθ
φθ
πφθφ
φ
φφθφθφ
u
v
v∆
u∆
ijR
),( vur
x
y
z
ur
vr
ijS

56. y)k)f(x,yjxiy)r(x,(
dA)
y
z
()
x
z
(1A(S)
isSofareasurfaceThe
D}y)(x,y),f(x,z|z)y,{(x,S2.
dArr
vu)r(r)A(SA(S)
vu|rr||rvru|)A(S
SofareaThe
D
22
D
vu
vuij
vuvuij
ij
++=
∂
∂
+
∂
∂
+=
∈==
×→
∆∆⋅×≈=
∆∆×=⋅∆×⋅∆≈
∫∫
∫∫
∑ ∑


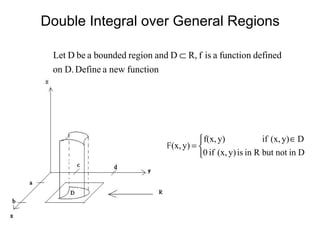
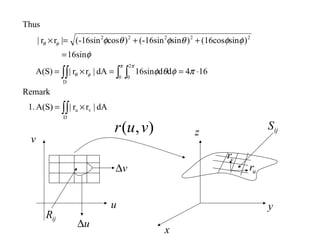
57. Triple Integrals
zwidthequalof]z,[[zlssubinterva
nintodividedaisf][e,y,widthequalof]y,[[ylssubinterva
mintodividedad]is[c,x,widthequalof]x,[xlssubinterval
intodividedisb][a,box.rrectangulaabef][e,d][c,b][a,BLet
:Definition
[0,2][1,3][0,1]B1.
:Example
f][e,d][c,b][a,
f}zed,ycb,xa|z)y,{(x,B
:boxrRectangula
k1-k
j1-j
i1-i
∆
∆
∆
××=
××=
××=
≤≤≤≤≤≤=

58. existslimitthisif
v)z,y,f(xlimz)dvy,f(x,
isBboxover thefofintergraltripleThe4.
v)z,y,f(xsumRiemanntripleThe3.
zyxvBofvolumeThe2.
]z,[z]y,[y]x,[xB1.
*
ijk
*
ijk
l
1i
m
1j
n
1k
*
ijk
B
0nm,l,
*
ijk
*
ijk
l
1i
m
1j
n
1k
*
ijk
ijk
k1-kj1-ji1-iijk
∆=
∆
∆⋅∆⋅∆=∆→
××=
∑∑∑∫∫∫
∑∑∑
= = =
→
= = =

59. ?yzdvxdefinetoHow
y}-x-1zx2,y01,x0|z)y,{(x,E3.
[0,2][1,3][-1,1]Bwhere,yz)dv(xEvaluate2.
[1,2][1,2][0,1]Bwhere,dvxyzEvaluate1.
:Example
z)dxdydzy,f(x,z)dvy,f(x,then
f][e,d][c,b][a,BoncontinuousisfIf
Theorem)sbini'Theorem(Fu
E
2
B
B
2
B
f
e
d
c
b
a
=
≤≤≤≤≤≤=
××=+
××=
=
××=
∫∫∫
∫∫∫
∫∫∫
∫∫∫ ∫ ∫ ∫

60. dydxz)dzy,f(x,z)dvy,f(x,then
y)}(x,zy)(x,(x),gy(x)gb,xa|z)y,{(x,EIf2.
dAz)dzy,f(x,z)dvy,f(x,then
y)}(x,zy)(x,D,y)(x,|z)y,{(x,EIf1.
properties
z)dvy,F(x,z)dvy,f(x,Define
Ez)y,if(x,0
Ez)y,if(x,z)y,f(x,
z)y,F(x,defineandE,B
boxrrectangulaaConsiderE.regionboundedgeneralaFor
E
b
a
g
g
2121
E D
21
E B
1(x)
1(x)
y)2(x,
y)1(x,
y)2(x,
y)1(x,
∫∫∫ ∫ ∫ ∫
∫∫∫ ∫∫ ∫
∫∫∫ ∫∫∫
=
≤≤≤≤≤≤=





=
≤≤∈=
=



∉
∈
=⊃
φ
φ
φ
φ
φφ
φφ

61. }x-yzx-y-4,yx2,x-2|z)y,{(x,E2.
zdzdydxzdv
y}-x-1z0x,-1y01,x0|z)y,{(x,E1.
:Examle
222
1
0
x-1
0
y-x-1
0
E
≤≤≤≤≤≤=
=
≤≤≤≤≤≤=
∫ ∫ ∫∫∫∫
x
z
y
22
zxy +=
15
128
dydzdxxzdvxz
4}yxz,x-4zx-42,-x-2|z)y,{(x,E
2
2-
x-4
x-4-
4
xz
22
E
22
2222
2
2 22
π
=+=+
≤≤+≤≤≤≤=
∫ ∫ ∫∫∫∫ +

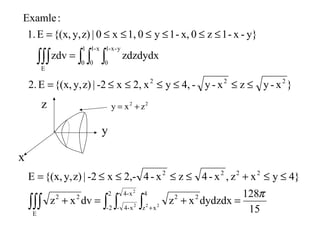
62. Riemann-Stieltjes Integral
integralStieltjes-Riemannnamely theintegral,generalmoreaconsiderWe
)18661826( − )18941856( −
integralRiemanntheofthatsimilar toisb][a,ong(x)
respect towithf(x)ofintegralStieltjes-RiemannThe
?f(x)dg(x)definetoHow2.
integralRiemannx)xf(limf(x)dx1.
:Remark
b
a
i
n
1i
i
0p||
b
a
∫
∑∫
=
←∆=
=
→

63. ∫
∑
∑
<
><
→∆→∆=
=
=∆∆=
=<<<<<=
=
=
=
b
a
n
1i
ii
i1-i
i1-iii
n
1i
ii
n1-n210
n10
|f(x)dg(x)-g)f,S(p,|
such that0aexiststhere0anyforif
b][a,ong(x)respect towithintegrableStieltjes-Riemannisf(x)2.
0pasMg)f(tg)f,S(p,1.
:Definition
n1,2,i],x,[xintervalin the
pointaistand)g(x-)g(xgwhere,g)f(tg)f,S(p,
g)f,S(p,sumtheDefinebxxxxxai.e
b][a,ofpartitionabe}x,x,{xPLet
ε
δε




64. ∫∫
∫∫
∫
∫
+
++
==∈
<∆
4
2-
x
2
0.5
3
1
x2
0
2
b
a
b
a
i1-ii
p
1)d(sinxe,cosxdlnx
1)de(x,1)dcosx(x1.
:Example
b][a,ong(x)to
respectwithfofintegralStieltjes-RiemannThe-f(x)dg(x)1.
:Notation
Mf(x)dg(x)n where1,2,i],x,[xpoint ttheof
choiceanyforand,normawithb][a,ofPpartitionanyfor
2
π
δ


65. 31)-(220)-(11])[x-]([xtlimxd[x]3.
0cos0)-(cos2
4
1
0
cos2x)
2
1
(-
2
1-
dxsin2x
2
1-
x2cosxsinxd
2
1
-)dxcosx(-sinxcosxdcosx2.
5
136
0
2
)xx
5
3
()dx3x(3xdx3x)1(x2))d(x1(x1.
:Example
(x)dxf(x)g'f(x)dg(x)
thenb],[a,on(x)g'derivativecontinuousahasg(x)where
b][a,ong(x)respect towithintegrableStieltjes-Riemannisf(x)thatSuppose
Theorem9.2
b][a,ong(x)respect towithintegrableStieltjes-Riemannisf(x)thenb][a,
oncontinuousisf(x)Ifb].[a,ong)(decreasinincreasingmonotonebeg(x)Let
Theorem9.1
n
1i
1-iii
2
0 0
0000
2
0
35242
2
0
23
2
0
2
b
a
b
a
p
=⋅+⋅==
===
===
=+=+=⋅+=++
=
∑∫
∫∫∫∫
∫∫∫
∫ ∫
=
→∆
π
π
ππππ

66. ∫ ∑=
+
=
=








=
≤≤
≤≤
≤≤
=
=<<<<=
b
a
i
n
1i
i1-i
n21
n1n
n1-nn
212
11
n21n21
))f(c-(f(x)dg(x)Then
,c,c,cat xcontinuousisandb][a,onboundedisf(x)If
xc,
cxc,
cxc,
cxa,
g(x)
such thatb,cccawhere,c,c,cat x
tiesdiscontinujumpwithb][a,ondefinedfunctionstepabeg(x)Let
Theorem9.3
λλ
λ
λ
λ
λ




67. 




<≤
<≤
<≤
=
4x3if2
3x1if4
1x0if1
g(x)1.
:Example
1 2 3 4
1
2
3
4
x
y
-152)-(22.54)-(231)-(41dg(x)x(iii)
34)-(421)-(41
))g(x-)(g(xtlimdg(x)x(ii)
-1518-34)-(231)-(41
))g(x-)(g(xtlimdg(x)x(i)
222
3.5
0
2
22
2
0
n
1i
1-ii
2
i
0
2
22
3
0
n
1i
1-ii
2
i
0
2
p
p
=++⋅=
=+⋅=
=
==+⋅=
=
∫
∫ ∑
∫ ∑
=
→∆
=
→∆

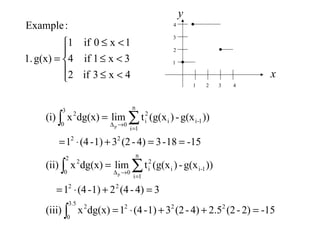
68. [0,1]on1)R(3xe12.
][0,on)R(xcosx1.
:Example
b][a,ong(x)respect to
withintegrableStieltjes-Riemannisfb][a,onR(g)f1.
:Notation
cos3cos2cos1
])[-]([cos2)-(3cos31)-(2cos20)-(1cos1
cosxd[x]cosxd[x]cosxd[x]cosxd[x]cosxd[x]
:Example
f(x)dg(x)f(x)dg(x)f(x)dg(x)f(x)dg(x)1.
:Remark
4x
2
3
3
2
2
10
1
0
c
c
c
c
b
a
c
a
2
n
1-n
2
1
1
+∈+
∈
≡∈
++=
+⋅+⋅+⋅=
+++=
+++=
∫∫∫∫ ∫
∫∫∫ ∫
π
πππ
ππ


69. ∫ ∫
∫ ∫ ∫
∫ ∫ ∫
=
∈∈
=+
=+
∈
b
a
b
a
2
0
2
0
222
c
a
b
c
b
a
g(x)df(x)-f(a)g(a)-f(b)g(b)f(x)dg(x)
haveweandb][a,onR(f)gthenb],[a,onR(g)fIf
Theorem9.5
cosxdxcosxdxcosxdx1.
:Example
f(x)dg(x)f(x)dg(x)f(x)dg(x)
haveweandexistsalsothirdthen the
exist,(1)inintegralsthreetheoftwoIfb),(a,cthatAssume
Theorem9.4
π π
π
π

70. incresingisg(x),(x)dg(x)fdg(x)(x)f(x)f(x)f7.
incresingisgdg(x),f(x)f(x)dg(x)6.
(x)f(x)dg(x)f(x)dg(x))g(x)f(x)d(g5.
(x)dg(x)f(x)dg(x)f(x))dg(x)f(x)(f4.
f(x)dg(x)kkf(x)dg(x)3.
f(x)dg(x)k)f(x)d(g(x)2.
g(a)-g(b)dg(x)1.
:Properties
b
a
2
b
a
121
b
a
b
a
b
a
2
b
a
1
b
a
21
b
a
2
b
a
1
b
a
21
b
a
b
a
b
a
b
a
b
a
∫∫
∫∫
∫∫∫
∫∫∫
∫ ∫
∫ ∫
∫
≤⇒≤
≤
+=+
+=+
=
=+
=

71. ∫
∫
∫
∫
∫
∫
∫
∫
=
=
+
=+
=+
=+
=
=
⋅=



≤<+
=
=∈
4
3
4
1
1
1-
6
0
2
5
0
x
5
0
2
4
6
1
0
2x
b
a
?[x]d[2x]8.
?
x
1-e1
1
|]dx[|7.
?|x-3|[x])d(x6.
?[x])d(xe5.
?)d[x]1(x4.
?xdtanx3.
?xde2.
hf(a)f(x)dg(x)thatShow
bxaifhc
axifc
g(x)b],c[a,f(x)let1.
:Exercise
π
π

72. ∫
∫
∫
∫
∫
∫
∫
∫



=
+
=



>
≤
==
+
→
2
0
2
0
2
0
2
1
t
1x
1
1-
0
4
5
4
1
4
5
4
1
exist?xdf(x)Does(iii)
existnotcanf(x)dxthatShow(ii)
existnotcanf(x)dxthatShow(i)
irrationalisxif1
rationalisxif0
f(x)Let14.
[t])d(telim13.
?|x|xd12.
2xif2
2xif0
g(x)where?cosxdg(x)11.
exist?[x]d[2x]Does10.
exist?[2x]d[x]Does9.
x
π