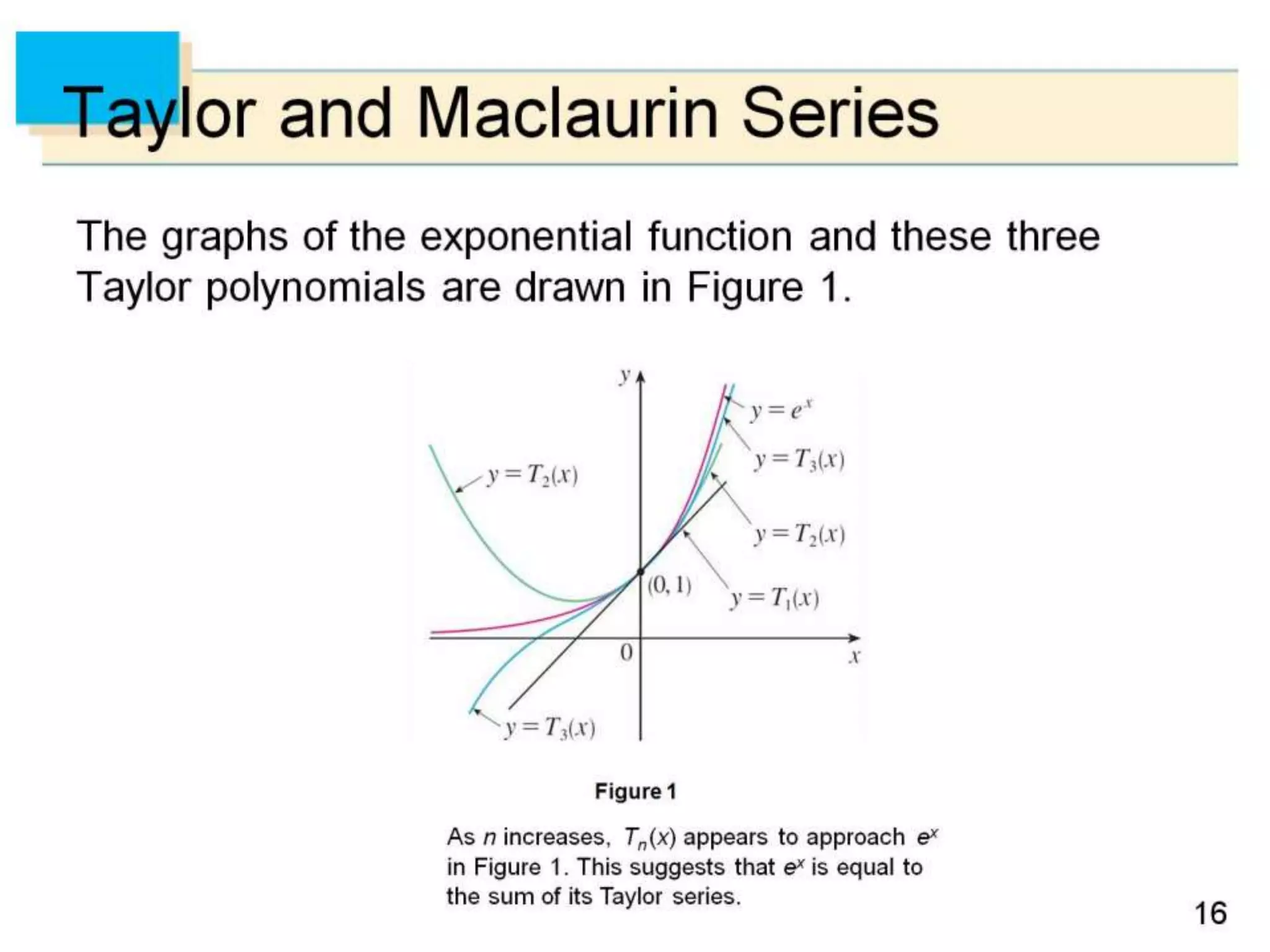
The document defines power series as sums of terms involving constants multiplied by powers of x, where x can be centered at 0 or another constant a. It states the convergence theorem for power series: if a power series converges at a point c ≠ 0, then it converges absolutely for all x within |c|, and if it diverges at a point d, then it diverges for all x outside |d|. It introduces the radius of convergence R, where a power series converges absolutely for |x-a|<R and diverges for |x-a|>R, regardless of what happens exactly at R.

27. DEFINATION
 A power series about x=0 is a series of the form
𝑛=0
∞
𝑐 𝑛 𝑥 𝑛
=𝑐0+𝑐1 𝑥 +𝑐2 𝑥2
+…….+𝑐 𝑛 𝑥 𝑛
+………
 A power series about x=a is a series of the form
𝑛=0
∞
𝑐 𝑛 (𝑥 − 𝑎) 𝑛
=𝑐0+𝑐1(𝑥 − 𝑎) +𝑐2(𝑥 − 𝑎)2
+….+𝑐 𝑛(𝑥 − 𝑎) 𝑛
+….
 In which the center a and the coefficieants 𝑐0, 𝑐1, 𝑐2,….,
𝑐n, … … … …
are constants.

28. THE CONVERGENCE THEOREM FOR
POWER SERIES
 If the power series 𝑛=0
∞
𝑎 𝑛 𝑥 𝑛=𝑎0+𝑎1 𝑥 +𝑎2 𝑥2+…….
Converges for x=c ≠0,then it converges absolutely for all x with
|x|<|c|. If the series diverges for x=d , then it diverges for all x
with |x|>|d|..

29. RADIUS OF CONVERGENCE
 In previous explainations there is a number R so that power
series will converge for , |x – a|< R and will diverge for |x –
a|> R.This number is called the radius of convergence for the
series.Note that the series may or may not converge if |x – a|
=R .What happens at these points will not change the radius
of cnvergencce.