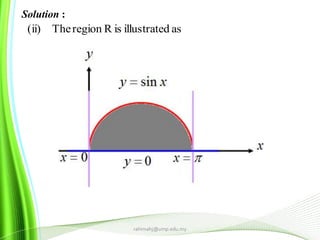
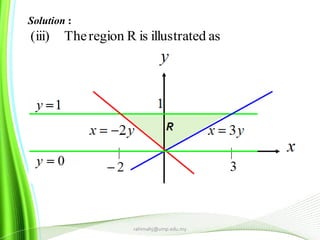
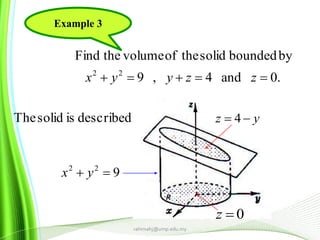
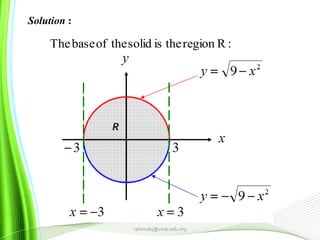
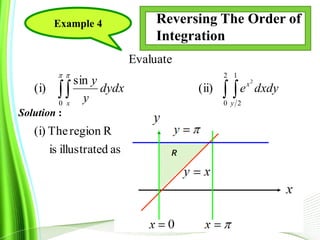
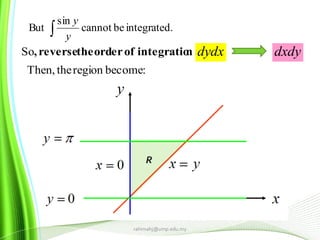
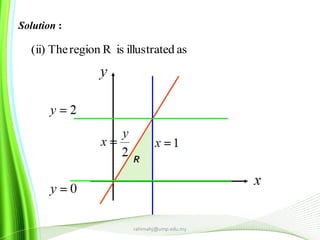
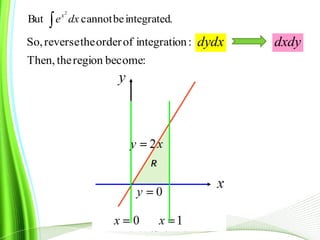
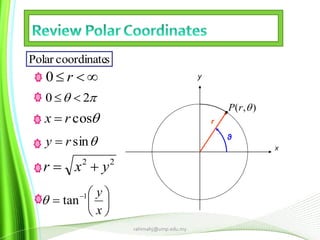
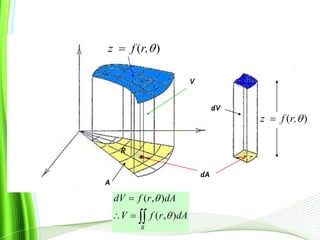
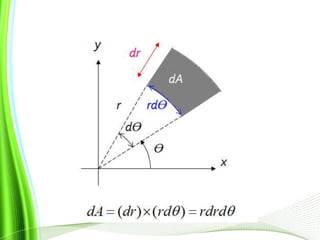
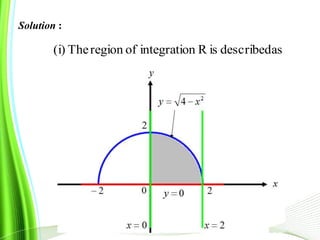
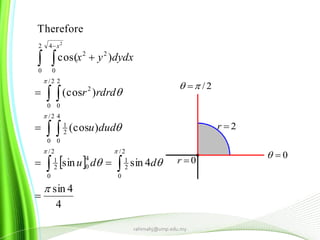
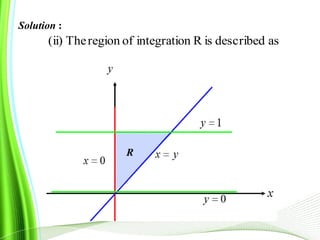
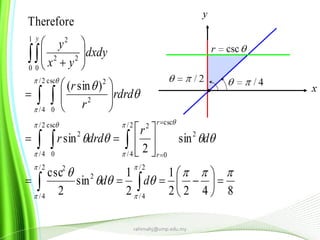
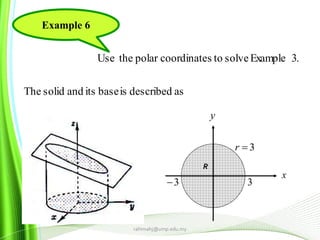
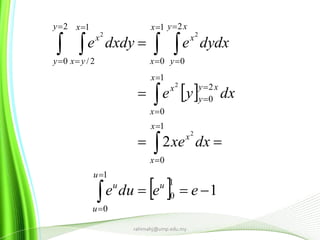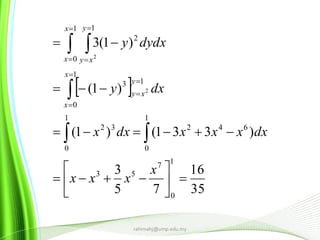This document provides information about multiple integrals and examples of evaluating them. It begins by defining multiple integrals and iterated integrals. It then gives 4 examples of evaluating double and triple integrals over different regions. These regions include rectangles, triangles, and solids. The document also discusses Fubini's theorem, which allows reversing the order of integration in certain cases. It concludes by providing an example of converting an integral from Cartesian to polar coordinates.


![
14
)1(2)2(226
])1()1(3[])1()1(3[
3)23(
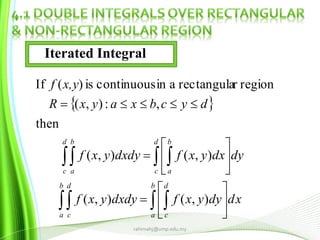
obtainweintegrals,iteratedofdefinitiontheUsing(i)
332
1
3
2
1
2
2
1
2222
2
1
1
1
22
2
1
1
1
2
xdxx
dxxxxx
dxxyyxdydxxyx
y
y
rahimahj@ump.edu.my
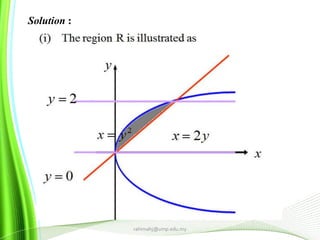
Solution :](https://image.slidesharecdn.com/chapter4multipleintegrals-150105021233-conversion-gate02/85/Applied-Calculus-Chapter-4-multiple-integrals-4-320.jpg)


![
5
36
5
2
4
2
)26(
]})(2[]2)2(2{[
2)4()4(
2
0
54
3
2
0
432
2
0
32222
2
0
22
2
0
2
2
2
yy
y
dyyyy
dyyyyy
dyxyxdxdyyxdAyx
yx
yx
y
y
yx
yxR
rahimahj@ump.edu.my](https://image.slidesharecdn.com/chapter4multipleintegrals-150105021233-conversion-gate02/85/Applied-Calculus-Chapter-4-multiple-integrals-10-320.jpg)