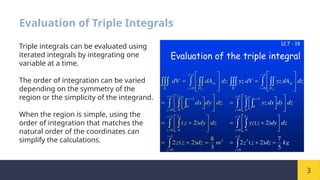
Triple integrals extend double integrals into three-dimensional space, used for calculating volume, mass, and average values of functions over a region. They can be evaluated through iterated integrals, with the order of integration adaptable to streamline calculations. Understanding their properties and methods of evaluation allows for effective use in various mathematical and physical applications.

1. Triple Integrals
SlideMake.com

2. 1
Introduction
Triple integrals are an extension of
double integrals in three dimensions.
They are used to calculate the volume,
mass, or average value of a function over
a three-dimensional region.
Triple integrals are denoted by f(x, y, z)
∭
dV, where f(x, y, z) is the integrand and
dV represents the infinitesimal volume
element.

3. 2
Triple Integral Bounds
The bounds of a triple integral define the
region of integration in three-
dimensional space.
The region can be defined using
Cartesian, cylindrical, or spherical
coordinates.
Cartesian coordinates: x_min x
≤ ≤
x_max, y_min y y_max, z_min z
≤ ≤ ≤ ≤
z_max.

4. 3
Evaluation of Triple Integrals
Triple integrals can be evaluated using
iterated integrals by integrating one
variable at a time.
The order of integration can be varied
depending on the symmetry of the
region or the simplicity of the integrand.
When the region is simple, using the
order of integration that matches the
natural order of the coordinates can
simplify the calculations.

5. 4
Applications of Triple Integrals
Volume calculation: Triple integrals can
be used to calculate the volume of
irregular shapes or solid objects.
Mass calculation: By incorporating a
density function into the integrand, triple
integrals can be used to calculate the
mass of an object.
Average value calculation: Triple
integrals can also be used to calculate
the average value of a function over a
three-dimensional region.

6. 5
Properties of Triple Integrals
Linearity: Triple integrals satisfy the
linearity property, allowing for easy
calculations when the integrand can be
expressed as a sum of multiple
functions.
Change of variables: Triple integrals can
be transformed using a change of
variables, which can simplify the
calculations or help to change the
coordinate system.
Symmetry: Sometimes, the symmetry of
the region or the integrand can be
exploited to simplify the triple integral.

7. 6
Conclusion
Triple integrals are powerful tools in
mathematics and physics for calculating
volumes, masses, and average values
over three-dimensional regions.
Understanding the bounds, evaluation
methods, and properties of triple
integrals is essential for their successful
application.
With practice and familiarity, triple
integrals can become a valuable tool in
solving a wide range of mathematical
and physical problems.