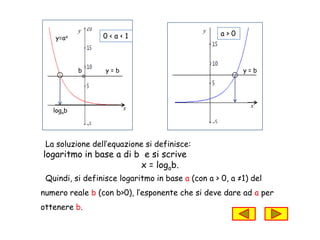
Il documento tratta la funzione esponenziale e il logaritmo, definendo le loro proprietà e relazioni. Viene spiegato che la funzione esponenziale è definita per un numero reale positivo diverso da uno e che il logaritmo è l'inverso dell'elevamento a potenza. Sono presentate le proprietà fondamentali dei logaritmi, tra cui il logaritmo del prodotto, quoziente e potenza, oltre alla dimostrazione del teorema del cambiamento di base.

1. Funzione esponenziale
Il Logaritmo. Proprietà

2. Dato un numero reale a positivo (a > 0 e a ≠ 1), si
definisce funzione esponenziale
la funzione che ad x R associa ax :
f: x-> ax (a > 0, a ≠ 1).
In base alla definizione, la funzione esponenziale ha come
dominio R e come codominio R+:
Dom: x (-∞; +∞ ); coDom: x (0; +∞ );

3. RIPASSO
Proprietà delle potenze: Proprietà inverse:
(a > 0, b > 0; R) (a > 0, b > 0; R)
1. a • a =a . 1. a =a • a
2. a :a = a . 2. a = a :a
3. (a ) = a . 3. a = (a ) = (a )
4. (a • b) = a • b 4. a • b = (a•b)
5. a = a . 5. a = a
b b b b
Casi particolari:
.a0 = 1;
.a-n = 1/an -> a -n - b n
b a

4. Bisogna distinguere i due casi:
1) 0 < a < 1; 2) a > 1.
1 caso: y = ax 0<a<1
la funzione y = ax risulta sempre
positiva:
ax > 0 , per Vx R.
ax1
e decrescente
per V x1, x2 con x1 < x2
ax2 ne segue ax > ax .
1 2
x1 x2

5. 2 caso: y = ax a>1
la funzione y = ax risulta sempre
positiva:
ax > 0 , per Vx R
ax2
e crescente:
per V x1 , x2, con x1 < x2
ax1
ne segue ax < ax .
1 2
x1 x2

6. In base alla definizione, la funzione esponenziale ha come
dominio R e come codominio R+:
Dom: x (-∞; +∞ ); coDom: x (0; +∞ );
1 1
y = ax 0<a<1 y = ax a>1

7. Equazioni esponenziali
Si definisce equazione esponenziale un’equazione in cui l’incognita
figura all’esponente, cioè un’equazione del tipo:
aP(x) = aQ(x)
Es.: 43x – 1 = 83 + x
Procedura risolutiva: si devono scrivere i due membri
dell’equazione sotto forma di potenze della stessa base.
22(3x – 1)= 23(3 +x) ; 26x – 2= 29 +3x ; da cui 6x – 2= 9 +3x .
Es.: 3x(3x-2) = 1
3x(3x-2) = 30 ; x(3x-2) = 0
3x+2 = 4•2x; 3x • 32 = 4•2x; 3x/2x= 32/22; (3/2)x = (2/3)-2; x = -2

8. Definizione di Logaritmo

9. Data l’equazione ax = b
si dimostra che, per a > 0, a ≠ 1 e b > 0, ammette una ed una
sola soluzione x R.
Dimostrazione grafica: l’equazione data si associa al sistema:
y = ax
y = b.
Graficamente la soluzione del sistema è rappresentata
dall’intersezione del grafico della funzione esponenziale y = ax
con la retta y = b. Tali grafici si intersecano in uno ed un solo
punto.

10. y
0<a<1
y
a >y=ax
0
y=ax
b y=b b y=b
logab x logab x
La soluzione dell’equazione si definisce:
logaritmo in base a di b e si scrive
x = logab.
Quindi, si definisce logaritmo in base a (con a > 0, a ≠1) del
numero reale b (con b>0), l’esponente che si deve dare ad a per
ottenere b.

11. Le basi dei logaritmi notevoli sono: la base 10, in questo caso,
convenzionalmente si scrive Log e si parla di logaritmi decimali;
la base e; in questo caso si scrive log oppure ln in questo caso
si parla di logaritmo neperiano o naturale.
Casi particolari:
loga a = 1; loga 1 = 0;
Esempi:
calcolare log2 8;
si indica log2 8 = x, da cui 2x=8, 2x = 23, quindi x=3.
calcolare log½ 8;
si indica log½ 8 = x, da cui (½)x=8, (½ )x = 23, (2)-x =23
quindi x=-3.

12. Dalla definizione di logaritmo si hanno le due seguenti
identità:
Per definizione di logaritmo logab = x (1)
si ha ax = b, (2)
1. ora, se si sostituisce b, dato dalla (2) nella (1), si ha:
loga ax= x
Questa identità si utilizza per scrivere un numero reale x in
forma logaritmica.
2. Se si sostituisce x, dato dalla (1) nella (2), si ha:
a logab = b,
Questa identità si utilizza per scrivere un numero reale
b, positivo, in forma esponenziale.

13. Proprietà dei logaritmi.
Prima proprietà:
Il logaritmo del prodotto di due numeri reali è uguale alla somma
dei logaritmi dei moduli dei due fattori.
loga(p•q) = loga|p| + loga|q|.
Osservazione: al 1 membro deve valere la condizione: p•q > 0;
il fatto che sia p•q > 0, implica la doppia
conseguenza:
o (p>0 e q>0) opp. (p<0 e q<0).
quindi, al secondo membro è necessario considerare il valore
assoluto di p e di q.

14. Seconda proprietà:
Il logaritmo del quoziente di due numeri reali è uguale alla
differenza dei logaritmi dei moduli dei due numeri.
loga( p ) = loga|p| - loga|q|.
q
Osservazione:al 1 membro deve essere p/q > 0;
il fatto che sia p/q > 0, implica la doppia
conseguenza:
o (p>0 e q>0) opp. (p<0 e q<0).
quindi al secondo membro è necessario considerare il valore
assoluto di p e di q.

15. Terza proprietà:
Il logaritmo della potenza di un numero reale positivo è uguale al
prodotto dell’esponente per il logaritmo della base della
potenza:
loga pk = klogap con p>0; k R
Es.:
loga n√pm = (m/n)logap .

16. Dimostrazione della 1A proprietà: supponendo p>0; q>0,
loga(p•q) = logap + logaq.
si sostituisce
loga p = x e loga q = y, (*)
Per la definizione di logaritmo risulta:
ax = p e ay = q , si moltiplicano membro a membro le due
uguaglianze: ax•ay = p•q, per la 1A proprietà delle potenze si ha:
ax + y = p•q.
In questa uguaglianza x + y rappresenta l’esponente che bisogna
dare ad a per ottenere p•q. Quindi per definizione di logaritmo,
risulta: x + y = loga (p•q).
Per le sostituzioni (*), si ha: loga p + loga q = loga (p•q).

17. Dimostrazione della 2A proprietà: supponendo p > 0; q > 0,
loga(p/q) = loga p - loga q.
si sostituisce
loga p = x e loga q = y, (*)
Per la definizione di logaritmo risulta:
ax = p e ay = q, si dividono membro a membro le due
uguaglianze: ax /ay = (p/q), per la 2A proprietà delle potenze si ha:
ax - y = p/q.
In questa uguaglianza x - y rappresenta l’esponente che bisogna
dare ad a per ottenere (p/q). Quindi per definizione di
logaritmo, risulta: x - y = loga (p/q).
Per le sostituzioni (*), si ha: loga p – loga q = loga (p/q).

18. Dimostrazione della 3A proprietà:
loga pk = klogap con p>0 e con k R
si sostituisce
logap = x (*)
Per la definizione di logaritmo risulta:
ax = p; si elevano entrambi i membri a potenza k :
(ax) k = pk,
per la 3A proprietà delle potenze si ha:
akx = pk.
In questa uguaglianza kx rappresenta l’esponente che, dato ad a,
dà come risultato pk. Quindi per definizione di logaritmo, risulta:
kx = loga pk
Per la sostituzione (*), si ha: kloga p = loga pk.

19. SCHEMA PROPRIETA’ DEI LOGARITMI
Proprietà dirette: Proprietà inverse:
loga(p•q) = loga|p| + loga|q|. logap + logaq = loga(p•q)
loga( p/q ) = loga|p| - loga|q|. loga p - loga q = loga( p/q )
loga pk = kloga |p|. kloga p = loga pk .
a>0; a≠1; k R a>0; a≠1; p>0; q>0; k R
o (p>0 e q>0) opp. (p<0 e q<0).

20. Teorema del cambiamento della base.
Passaggio dal logaritmo in base a di un numero b
al logaritmo in base k di b.
Il logaritmo in una nuova base k del numero b è uguale al
rapporto tra il logaritmo nella base a, di partenza, di b e il
logaritmo nella base di partenza a della nuova base k:
logab
logkb=
logak
a>0, a≠1; b>0, b≠1; k>0, k≠1;

21. Dimostrazione del teorema.
Si pone
logkb = x (*)
per definizione di logaritmo, risulta: kx = b;
ora si calcola il logaritmo in base a di entrambi i membri:
loga kx = loga b,
per la proprietà del logaritmo di una potenza, risulta:
x• loga k = loga b
per la sostituzione (*):
logkb • loga k = loga b
da cui, ricavando logkb, il teorema:
logab
logkb=
logak

22. Caso particolare. Se si pone: b = a
logab
logkb=
logak
La relazione diventa:
logaa
logka=
logak
Da cui:
1 Cioè, scambiando la base k del logaritmo
logka= con il suo argomento a, si ottiene il
logak reciproco del logaritmo in base a di k.

23. La Funzione Logaritmo
Dato un numero reale a positivo (a > 0 e a ≠ 1), si
definisce funzione logaritmica
la funzione che ad x R+ associa logax :
f: x -> logax (a > 0, a ≠ 1; x > 0).
y = logax
In base alla definizione, la funzione logaritmica ha come
dominio R+ e come codominio R:
Dom: x (0; +∞ ); coDom: x (-∞ ; +∞ );

24. Nella definizione di funzione esponenziale:
y = ax , x rappresenta l’esponente che bisogna dare ad a per
ottenere y; questa è la definizione di logaritmo in base a di y:
x = logay.
La funzione esponenziale risulta invertibile.
Ora il grafico di x = loga y coincide con quello di y = ax.
Ma se si opera lo scambio di variabili x <=> y, allora si ottiene
y = logax.
Quindi il grafico della funzione logaritmica risulta
simmetrico del grafico di y = ax, rispetto alla bisettrice del 1
e 3 quadrante.

25. In base alla definizione di logaritmo, si deduce che si tratta
dell’operazione inversa dell’elevamento a potenza.
y = ax y=x
y = ax, a>1
y = logax
y = logax, a>1

26. y = a x, 0<x<1
y=x
y = logax, 0 <a< 1

27. y = logax, 0 <a< 1
y = logax, a>1

28. Esercizio.
Le funzioni:
f(x) = log(x-1)2 e g(x) = 2log(x-1)
Sono la stessa funzione? Spiegare.
Non sono la stessa funzione.
Infatti, le due funzioni hanno domini diversi:
Domf(x): (x-1)2 > 0 -> V x ≠ 1. x {(-∞; 1) v (1; +∞)}
Domg(x): x – 1 > 0 -> x > 1. x (1; +∞).
Per rendere le due funzioni identiche si deve scrivere:
g(x) = 2log|x-1|
tenendo presente la terza proprietà.

29. Calcolare il dominio della funzione:
f(x) = log(x2-1) (2x2 – 3x)
Si tratta di una funzione logaritmica di base (x2-1)
e argomento (2x2 -3x).
Primo modo:
Per la definizione di logaritmo, occorre porre le condizioni sulla
base :
(x2 – 1) > 0 e x2 – 1 ≠ 1
e sull’argomento del logaritmo:
(2x2 – 3x) > 0
Quindi si tratta di risolvere il sistema:
x2 – 1 > 0
x2 – 1 ≠ 1.
2x2 – 3x > 0

30. Secondo modo:
Si applica il teorema del cambiamento di base per scrivere la
funzione nel seguente modo:
f(x) = log (2x2 – 3x)
log (x2- 1)
Si hanno le condizioni sugli argomenti dei due logaritmi:
(2x2 – 3x) > 0; x2 – 1 > 0
E la condizione sul denominatore:
log (x2- 1) ≠ 0 cioè (x2- 1) ≠ 1
Quindi si ritrova il sistema precedente:
x2 – 1 > 0
x2 – 1 ≠ 1.
2x2 – 3x > 0