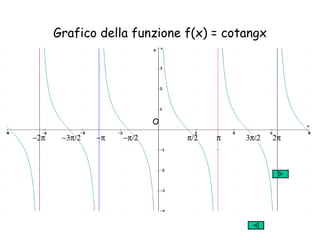
Il documento tratta della goniometria, coprendo le misure di angoli e archi, la definizione di radiante, e le funzioni goniometriche come seno, coseno e tangente. Vengono presentate le relazioni tra misure in radianti e gradi, nonché i valori notevoli di seno e coseno per angoli specifici. Infine, il documento esplora la definizione e le variazioni delle funzioni tangente e cotangente in relazione alla circonferenza goniometrica.

1. GONIOMETRIA. MISURE DI ANGOLI ED ARCHI LE FUNZIONI GONIOMETRICHE.

2. Definizione di misura in radianti di un arco di circonferenza. Dalla definizione di misura in radianti di un arco si ricava la misura dell’arco di crf.nza: Dato un arco di circonferenza AB, si definisce misura in radianti dell’arco il rapporto tra la misura dell’arco rettificato l (rett) e il raggio r della circonferenza: l (rett) = r α rad α rad l A B O r r arco (rettificato) l (rett) α rad = = raggio r

3. Premessa. Teorema. Archi di circonferenze aventi la stessa ampiezza sono proporzionali ai raggi delle corrispondenti crf.nze. α r 1 r 2 r 3 r n l n l 3 l 2 l 1 l 1 l 2 l 3 l n = = =…= r 1 r 2 r 3 r n

4. α O Dal teorema precedente si perviene alla definizione di misura in radianti di un angolo. l Dato l’ angolo ab , di vertice O, si considera una circonferenza di centro O. (1clic) a b Si definisce misura in radianti dell’angolo ab la misura in radianti dell’arco l di crf.nza. L’angolo intercetta sulla circonferenza un arco l . (1clic) l (rett) α rad = r

5. Relazione tra misura in radianti e in gradi sessagesimali. Premessa. Gli archi di una stessa circonferenza o di crf.nze congruenti sono proporzionali alle rispettive ampiezze. l 1 : l 2 = α 1 : α 2 Data una circonferenza, consideriamo come arco l 1 l’intera circonferenza, quindi la sua ampiezza è di 360° e come arco l 2 un arco l ampio α ° gradi. La proporzione diventa: 2 π r : l = 360° : α ° Dividendo i termini del primo rapporto per r , si ha: 2 π r l : = 360° : α ° r r

6. si ottiene: 2 π : α rad = 360° : α ° e, dividendo per 2 gli antecedenti, si ha la regola di conversione tra i gradi e i radianti: Per la definizione di misura in radianti di un arco: π : α rad = 180°: α ° 180° α ° = α rad π l (rett) α rad = r π α rad = α ° 180°

7. Misura in radianti di angoli notevoli. Se si considera l’angolo di ampiezza 360°, esso individua su una circonferenza un arco pari alla crf.nza stessa. Siccome la crf.nza rettificata misura 2 π r, si ha: Di conseguenza si ricavano i seguenti valori notevoli: crf (rettificata) 2 π r α rad = = = 2 π rad raggio r r 360° GRADI RADIANTI 180° π 90° π 2 45° π 4 GRADI RADIANTI 120° 2 π 3 60° π 3 30° π 6

8. Definizione geometrica di seno, coseno di un arco (angolo) In un sistema di assi cartesiani e si considera la circonferenza di centro O e raggio 1 (crf.nza goniometrica). Dato un arco  , si considera l’arco di crf.nza AP =  , avente il primo estremo nel punto A(1;0); sia P(x;y) il secondo estremo di tale arco. Definizione : si definiscono coseno e seno dell’arco (oppure dell’angolo) ampio  rispettivamente l’ascissa e l’ordinata del punto P, quindi si può scrivere: P(cos  ; sen  )

9. Dato l’arco di circonferenza AP=  , considerando il triangolo rettangolo OPH (in figura), si constata che le misure dei cateti coincidono con le coordinate del punto P della crf.nza goniometrica mentre l’ipotenusa OP è uguale al raggio 1 della crf.nza. (1clic) x y O A(1;0) H PH = y P = sen  . OH = x P = cos  . OP = 1 P(x;y) y P x P  

10. Seno e Coseno O x y  cos  sen  P(x;y) P( cos  ; sen  ) A(1;0) 

11. Valori notevoli di Seno e Coseno   4   6   3 Ricordando le regole dei triangoli rettangoli con un angolo acuto rispettivamente di 30°; 45°; 60°: si ha la tabella:    6   4   3 1clic   6 ½ √ 3 2 1   4 √ 2 2 √ 2 2 1   3 √ 3 2 ½ 1 x y seno coseno ½ √ 2 2 √ 3 2 √ 2 2 ½ √ 3 2

12. Valori notevoli degli archi (angoli) da 0 a 2 π rad. 2  3   2   4   6   3 3  4 5  6 7  6 5  4 4  3 3  2 5  3 7  4 11  6    1 clic Verso positivo degli archi

13. Valori notevoli degli archi (angoli) da 0 a -2 π rad. - 2  3    2    4    6    3 - 3  4 - 5  6 - 7  6 - 5  4 - 4  3 - 3  2 - 5  3 - 7  4 - 11  6  0 -2  1 clic Verso negativo degli archi

14. Variazioni di Seno e Coseno 1°quadr. Se 0 <  < ½  P possiede ascissa POSITIVA e ordinata POSITIVA. Quindi cos  >0 e sen  >0 x P >0; y P >0 x P <0; y P >0 x P >0; y P <0 x P <0; y P <0 2°quadr. Se ½        P  possiede ascissa NEGATIVA e ordinata POSITIVA. Quindi cos  <0 e  sen  0 3°quadr. Se      (3/2)  P possiede ascissa NEGATIVA e ordinata NEGATIVA. Quindi cos  <0 e  sen  0 4°q. Se (3/2)          P  possiede ascissa POSITIVA e ordinata NEGATIVA. Quindi cos  >0 e  sen  0 1CLIC 1CLIC 1CLIC 1CLIC O x y P(x P ;y P ) A    2 3  2   

15. In conclusione: al variare di  da 0 rad. a 2  rad. sia il seno che il coseno di  variano tra -1 e +1 (compresi tali valori) 0 <  < ½  ½        <  < ( 3/2)  (3/2)  <  < 2  Seno 0 < sen  <  1 < sen  < 0 0 < sen  <  -1 -1 < sen  <  0 Coseno 1 < cos  <  0 0 < cos  <  -1 -1 < cos  < 0 0 < cos  <  1

16. Prima Identità Fondamentale Ma, d’altra parte, abbiamo visto che: x P =cos  , y P =sen  Quindi, sostituendo nella relazione (1), si ottiene: Siccome il punto P(x P ;y P ), introdotto per definire il seno e il coseno dell’arco  , appartiene alla circonferenza goniometrica, le sue coordinate devono soddisfare l’equazione di tale circonferenza, cioè: x P 2 + y P 2 = 1 (1) sen 2  + cos 2  = 1 O x y P(x P ;y P ) A(1;0) 

17. Definizione di Tangente di un arco (angolo) In un sistema di assi cartesiani e si considera la circonferenza di centro O e raggio 1 (crf.nza goniometrica). Dato un arco  , si considera l’arco di crf.nza AP =  , avente il primo estremo nel punto A(1;0); sia P(x;y) il secondo estremo di tale arco. Si traccia la retta tangente alla circonferenza goniometrica nel suo punto A(1;0) e si considera l’intersezione con la retta OP. Detto T tale punto di intersezione, si definisce tangente dell’arco AP l’ordinata del punto T .

18. Tangente x y O x=1 T(1;y)  tang  T(1;tang  ) A(1;0) 1clic P 

19. Campo di Esistenza della Tangente Risulta evidente che la retta per O e P interseca la retta x=1, tangente in A, se e solo se non è parallela a tale retta. Questo fatto si verifica se P coincide con B opp. con C (vedi in fig.) cioè se:  =   oppure    =  3     2  2 Quindi la definizione di tangente di  ha senso se e solo se:  ≠   e    ≠  3     2  2 O x y P A(1;0)  B C x=1 T ¤ ¤

20. Variazioni della Tangente Se 0 <  < ½  (cioè: se P appartiene al 1° quadrante) La tangente varia da 0 a +∞ Se ½       (cioè: se P appartiene al 2° quadr.) La tangente varia da -∞ a  0  . P’’’ Se        . (cioè: se P appartiene al 3° quadr.) La tangente varia da 0 a +∞ Se  3/2      2  . (cioè: se P appartiene al 4° quadr.) La tangente varia da -∞ a  0  . O x y P A(1;0)  B C x=1 T ¤ ¤ P’ P’’ T’

21. Sintesi grafica delle definizioni  x y O x=1 T(1;y)  A(1;0) cos  P(x;y) T(1;tang  ) P(cos  ;sen  ) 1clic tang  sen  

22. I triangoli OAT e OHP sono simili essendo rettangoli e avendo l’angolo in O in comune (1°criterio di similitudine). Si ha la seguente proporzione: AT : AO = PH : OH Sostituendo le misure dei lati: si perviene alla relazione: sen  tang  =  cos  Seconda identità fondamentale T A(1;0) P x y H O cos  sen  tang  PH = sen  OH = cos  AT = tang  OA = 1

23. Definizione di cotangente di un angolo In un sistema di assi cartesiani e si considera la circonferenza di centro O e raggio 1 (crf.nza goniometrica). Dato un arco  , si considera l’arco di crf.nza AP =  , avente il primo estremo nel punto A(1;0); sia P(x;y) il secondo estremo di tale arco. Si traccia la retta tangente alla circonferenza goniometrica nel suo punto B(0;1) e si considera l’intersezione con la retta OP. Detto T tale punto di intersezione, si definisce cotangente dell’arco AP l’ascissa del punto T .

24. Cotangente x y O  T(cotang  ) A(1;0) 1clic B(0;1) y = 1 P 

25. Variazioni della Cotangente Se 0 <  < ½  (cioè: se P appartiene al 1° quadrante) La cotangente varia da +∞ a   Se ½        (cioè: se P appartiene al 2° quadr.) La cotangente varia da 0  a -∞ Se        . (cioè: se P appartiene al 3° quadr.) La cotangente varia da +∞ a  Se  3/2        2  . (cioè: se P appartiene al 4° quadr.) La cotangente varia da  0 a -∞  O x y P A(1;0)  D y=1 T B ¤ ¤ T’ P’ P’’’ P’’

26. Campo di Esistenza della Cotangente Risulta evidente che la retta per O e P interseca la retta y=1, tangente in B, se e solo se non è parallela a tale retta. Questo fatto si verifica se P coincide con A o con D (vedi in fig.) cioè se:  =  =  =    Quindi la definizione di cotangente di  ha senso se e solo se:  ≠ 0  ≠  ≠    O x y P A(1;0)  D y=1 T B ¤ ¤

27. Definizioni di Cosecante Secante Dato l’arco AP =  , per il punto P si traccia la retta tangente alla crf.nza goniometrica. Tale retta interseca l’asse delle ordinate nel punto S. Si definisce cosecante dell’arco  , l’ordinata del punto S . Quindi si può scrivere : S(O; cosec  ) La stessa retta tangente interseca l’asse delle ascisse nel punto C.  Si definisce secante dell’arco  , l’ascissa del punto C . Quindi si può scrivere: R( sec  ; 0) x O  A(1;0) P y S R

28. Campo di esistenza della Cosecante Risulta evidente che la retta tangente in P interseca l’asse delle ordinate y se e solo se non è parallela a tale asse. Questo fatto si verifica se P coincide con A o con D (vedi in fig.) cioè se: S(0; cosec    =  =  =    Quindi la definizione di cosecante ha senso se e solo se:  ≠ 0  ≠  ≠    O x y P A(1;0)  D B ¤ ¤

29. Variazioni della Cosecante Se 0 < a < ½  e ½        . (cioè: se P appartiene al 1° opp. al 2° quadrante) La cosecante varia, rispettivamente da + ∞ a 1 (1°quadr.); e da 1 a + ∞ (2°q.) Se       e         . (cioè: se P appartiene al 3° opp. al 4° quadrante) La cosecante varia da -∞ a  -1 (3°quadr.) e da -1 a   ∞ ∞ (4°q.) O x y P A  D B ¤ ¤ S(0; cosec  

30. Campo di esistenza della Secante Risulta evidente che la retta tangente in P interseca l’asse delle ascisse x se e solo se non è parallela a tale asse. Questo fatto si verifica se P coincide con B o con C (vedi in fig.) cioè se: Quindi la definizione di secante ha senso se e solo se:  =   oppure    =  3     2  2  ≠   e    ≠  3     2  2 O x y P A  C B ¤ ¤ R( sec  

31. Variazioni della secante Se 0 < a < ½  . (cioè: se P appartiene al 1°quadrante) La secante varia da 1 a + ∞ Se        . (cioè: se P appartiene al 4° quadr.) La secante varia da +∞ a 1 . ∞  Se ½       (cioè: se P appartiene al 2° quadr.) La secante varia da -∞ a   -  Se          (cioè: se P appartiene al 3° quadr.) La secante varia da -1 a - ∞  O x y P A  C B ¤ ¤ R(0; sec   R’

32. Relazioni tra Seno,Coseno e Cosecante, Secante x O  cos  sen  A(1;0) P y S C Dato l’arco AP = a, per il punto P si traccia la retta tangente alla crf.nza goniometrica. Applicando il primo teorema di Euclide al triangolo rettangolo OPS si ha: OS: OP = OP : OQ Sostituendo le misure: OS : 1 = 1 : sen  , H Q Applicando il primo teorema di Euclide al triangolo rettangolo OPC si ha: OC : OP = OP : OH Quindi: 1 OS = = cosec  . sen  Quindi: 1 OC = = sec  . cos 

33. Funzioni dirette e reciproche Seno Cosecante Coseno Secante Tangente Cotangente

34. Archi associati Si definiscono archi associati gli archi:  Se l’angolo  è acuto, gli archi associati hanno il secondo estremo coincidente con un vertice di un rettangolo inscritto nella crf.nza goniometrica e avente i lati paralleli agli assi.      

35. Funzioni goniometriche di  Funzioni goniometriche di  sen(  ) = sen  cos(  ) = -cos  tg(  ) = -tg  cotg(  ) = -cotg  sen(  ) = -sen  cos(  ) = -cos  tg(  ) = +tg  cotg(  ) = +cotg 

36. Funzioni goniometriche di  Funzioni goniometriche di  sen(2  ) = -sen  cos(2  ) = +cos  tg(2  ) = -tg  cotg(2  ) = -cotg  sen(  ) = -sen  cos(  ) = +cos  tg(  ) = -tg  cotg(  ) = -cotg 

37. In conclusione. Le funzioni goniometriche degli angoli:         in valore assoluto, coincidono con le stesse funzioni di  . Regola pratica: Per quanto riguarda il segno occorre considerare in quale quadrante si trovano i secondi estremi degli archi, a partire dal quadrante in cui  si trova.

38. Altri archi (angoli) particolari x y Altri archi (angoli) associati ad  :  il complementare di  )  e  inoltre:     2    2   2 3  2 3  2 3  2   2 3  2

39. sen = +cos  cos =+sen  tang = +cotg  cotg =+tang  sen = +cos  cos = -sen  tang =-cotg  cotg =-tang  Funzioni goniom. di  Funzioni goniom. di    2   2   2   2   2   2   2   2   2   2

40. Funzioni goniom. di  Funzioni goniom. di  3  2 3  2 sen = -cos  cos =-sen  tang = +cotg  cotg =+tang  sen = -cos  cos = +sen  tang =-cotg  cotg =-tang  3  2 3  2 3  2 3  2 3  2 3  2 3  2 3  2

41. In conclusione. Le funzioni goniometriche degli archi (angoli):  in valore assoluto, coincidono con le rispettive cofunzioni goniometriche di  . [seno <-> coseno; tangente <-> cotangente] Regola pratica: Per quanto riguarda il segno occorre considerare in quale quadrante si trovano i secondi estremi degli archi, supponendo che  si trovi nel primo quadrante. (ad es.: supponendo   1°q. ->   2°q.;    3°q.)   2 3  2   2 3  2

42. TABELLA VALORI DELLE FUNZIONI GONIOMETRICHE PER ARCHI NOTEVOLI seno 0 1 coseno tangente cotg.nte   2   4   6   3 0 √ 2 2 √ 3 2 √ 2 2 √ 3 2 √ 3 3 √ 3 √ 3 √ 3 3 ½ ½ 1 0 1 1 0 0  

43. 1clic 1clic √ 2 2 - √3 2 - √3 2 - √3 2 + √3 2 √ 3 2 √ 3 2 √ 2 2 - √2 2 √ 2 2 - √2 2 - √2 2 - √2 2 √ 2 2 rad sen cos tg ctg 2  3   2   4   6   3 3  4 5  6   √ 3 2 ½ 1 √ 3 3 0 0 -1 0 0 √ 3 1 1  ½ √ 3 √ 3 3 1 0  √ 3 2 ½ - √3 3 -√3 -1 -1  0 -½ -√3 - √3 3 rad sen cos tg ctg 5  3 3   2 5   4 7   6 4   3 7  4 11  6 2  - ½ + √3 3 +1 0 0 +√3 +1 +1 - ½ √ 3 √ 3 3 -1 0  -½ - √3 3 -√3 -1 -1  0 + ½ -√3 - √3 3

44. Grafico della funzione f(x) = senx         O

45. Grafico della funzione f(x) = cosx        O 

46. Grafico della funzione f(x) = tangx        O 

47. Grafico della funzione f(x) = cotangx O        

48. Grafico della funzione f(x)=cosecx

49. Grafico di f(x)= secx x O y = 1 y = -1