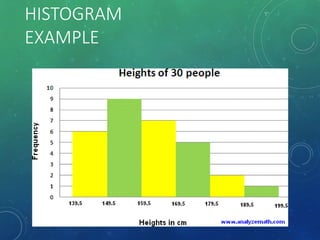
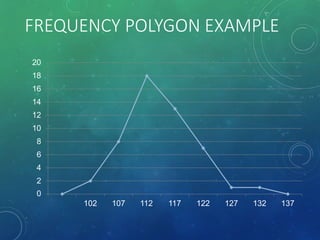
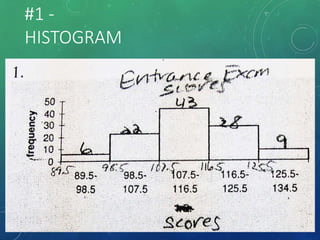
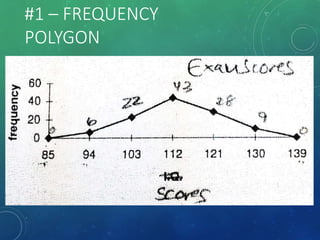
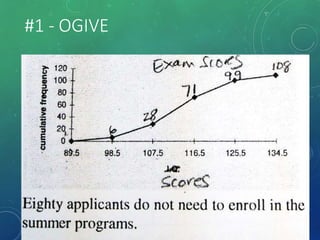
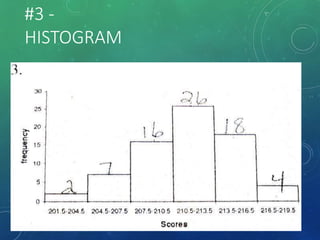
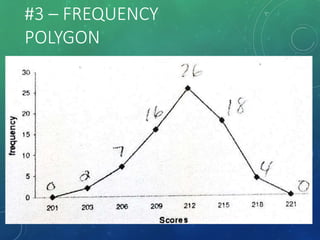
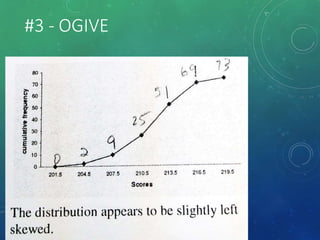
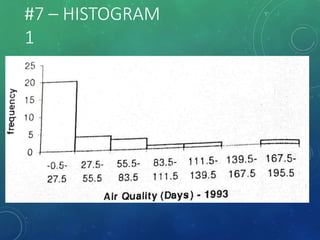
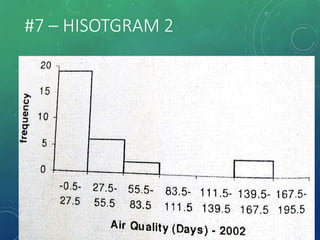
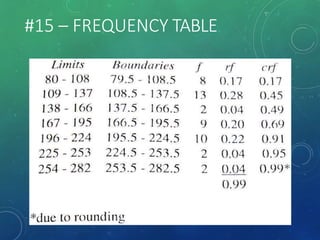
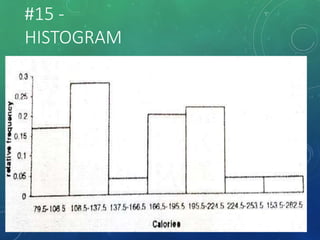
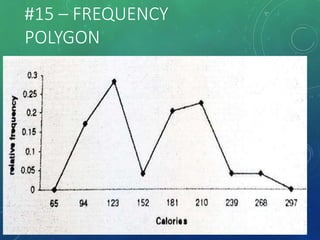
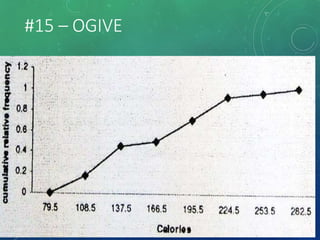
The document provides an overview of graphical representations of frequency distributions, including histograms, frequency polygons, and ogives. It outlines the construction methods for each type of graph, their purposes, and various distribution shapes. The objective is to effectively analyze and summarize data while engaging the audience visually.

1. FACULTY OF EDUCATION
ELSA QAZI CAMPUS
PREPAIRED BY : KUBRA
SEAT NO: 28
TOPIC: Frequency polygon
ASSIGNED BY:
DR. AMJAD ALI ARAIN

2. OBJECTIVE
:
 To represent data in frequency distributions
graphically using histograms, frequency
polygons, and ogives.
a] What % of Americans find life dull?
b] What % of Americans are color blind?
c] How many gallons of soda does the average
American drink during a year?

3. GRAPHS
 Purpose: To display data to viewer in pictorial
form
 Used to: Describe or analyze data
Discuss an issue
Reinforce a critical point
Summarize a data set
Discover a pattern or trend over time
 Useful in getting the attention of the audience

4. THREE MOST COMMON TYPES OF GRAPHS
 Histogram
 Frequency Polygon
 Cumulative Frequency Graph (Ogive)

5. HISTOGRAM
 histogram: graph that displays the data by
using contiguous vertical bars (unless the
frequency of a class is 0) of various heights to
represent the frequencies of the classes
 To construct a histogram:
Draw and label the x and y axes.
Represent the frequency on the y-axis and the
class boundaries on the x-axis.
Using the frequencies as heights, draw vertical
bars for each class.

6. HISTOGRAM
EXAMPLE

7. FREQUENCY POLYGON
 frequency polygon: graph that uses lines that connect
points plotted for the frequencies at the midpoints of
the classes; frequencies are represented by the
heights of the points
 To construct a frequency polygon:
Find the midpoints of each class
Draw the x and y axes. Label the x-axis with the midpoint
of each class then use a suitable scale for the frequencies
on the y-axis.
Using the midpoints for the x values and the frequencies
as the y values, plot the points.
Connect adjacent points with line segments. Draw a line
back to the x-axis at the beginning and end of the graph
(where the next midpoints would be located)

8. FREQUENCY POLYGON EXAMPLE
20
18
16
14
12
10
8
6
4
2
0
102 107 112 117 122 127 132 137

9. THE OGIVE (CUMULATIVE FREQUENCY POLYGON)
 ogive: graph that represents the cumulative
frequencies for the classes in a frequency
distribution
 To construct an ogive:
Find the cumulative frequency for each class
Draw the x and y axes. Label the x-axis with the class
boundaries. Label the y-axis with an appropriate
frequency (don’t use actual frequency numbers-yields
uneven intervals or classes)
Plot the cumulative frequency at each upper class
boundary
Starting with the first upper class boundary, connect
adjacent points with line segments. Extend the graph
to the first lower class boundary on the x-axis.

10. CONSTRUCTING STATISTICAL GRAPHS- GENERAL
PROCEDURES
 Draw and label the x and y-axes
 Choose a suitable scale for the frequencies or
cumulative frequencies, and label it on the y-
axis.
 Represent the class boundaries for the
histogram or ogive, or the midpoint for the
frequency polygon, on the x-axis.
 Plot the points and then draw the bars or lines.

11. DISTRIBUTION
SHAPES
 Bell-shaped: single peak and tapers off at either end
 Uniform: basically flat or rectangular
 J-Shaped: Few data values on the left side and
increases as one moves to the right
 Reverse J-Shaped: Opposite of J-Shaped
 Right-Skewed: Peak of the distribution is to the left
and the data values taper off to the right (Positively
skewed)
 Left-Skewed: Data values are clustered to the right
and taper off to the left (Negatively skewed)
 Bimodal: Two peaks of the same height
 U-Shaped: Peaks at both ends and decreases

12. #1 -
HISTOGRAM

13. #1 – FREQUENCY
POLYGON

14. #1 - OGIVE

15. #3 -
HISTOGRAM

16. #3 – FREQUENCY
POLYGON

17. #3 - OGIVE

18. #7 – HISTOGRAM
1

19. #7 – HISOTGRAM 2

20. #15 – FREQUENCY TABLE

21. #15 -
HISTOGRAM

22. #15 – FREQUENCY
POLYGON

23. #15 – OGIVE

24. THANKS YOUR SIR