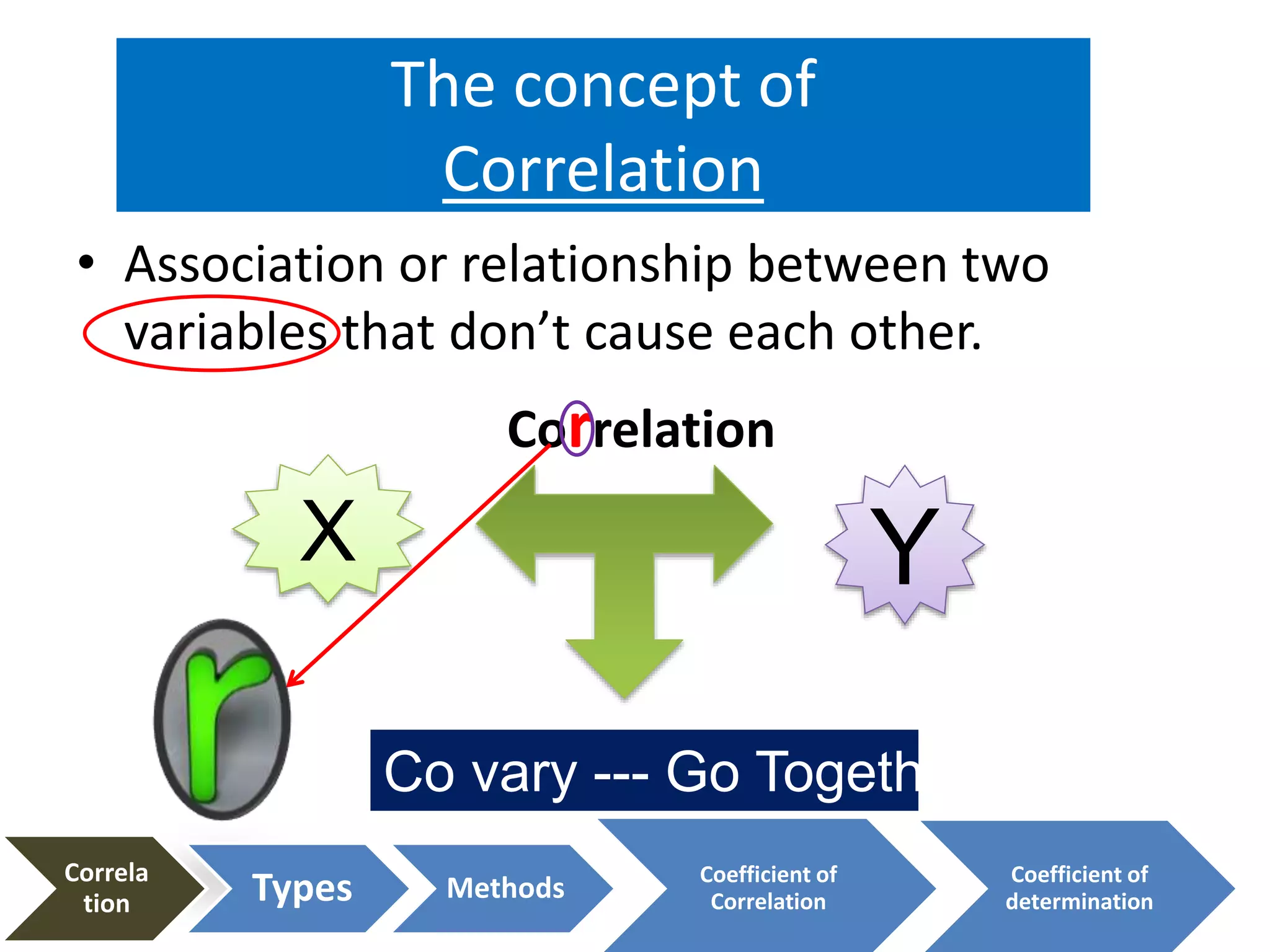
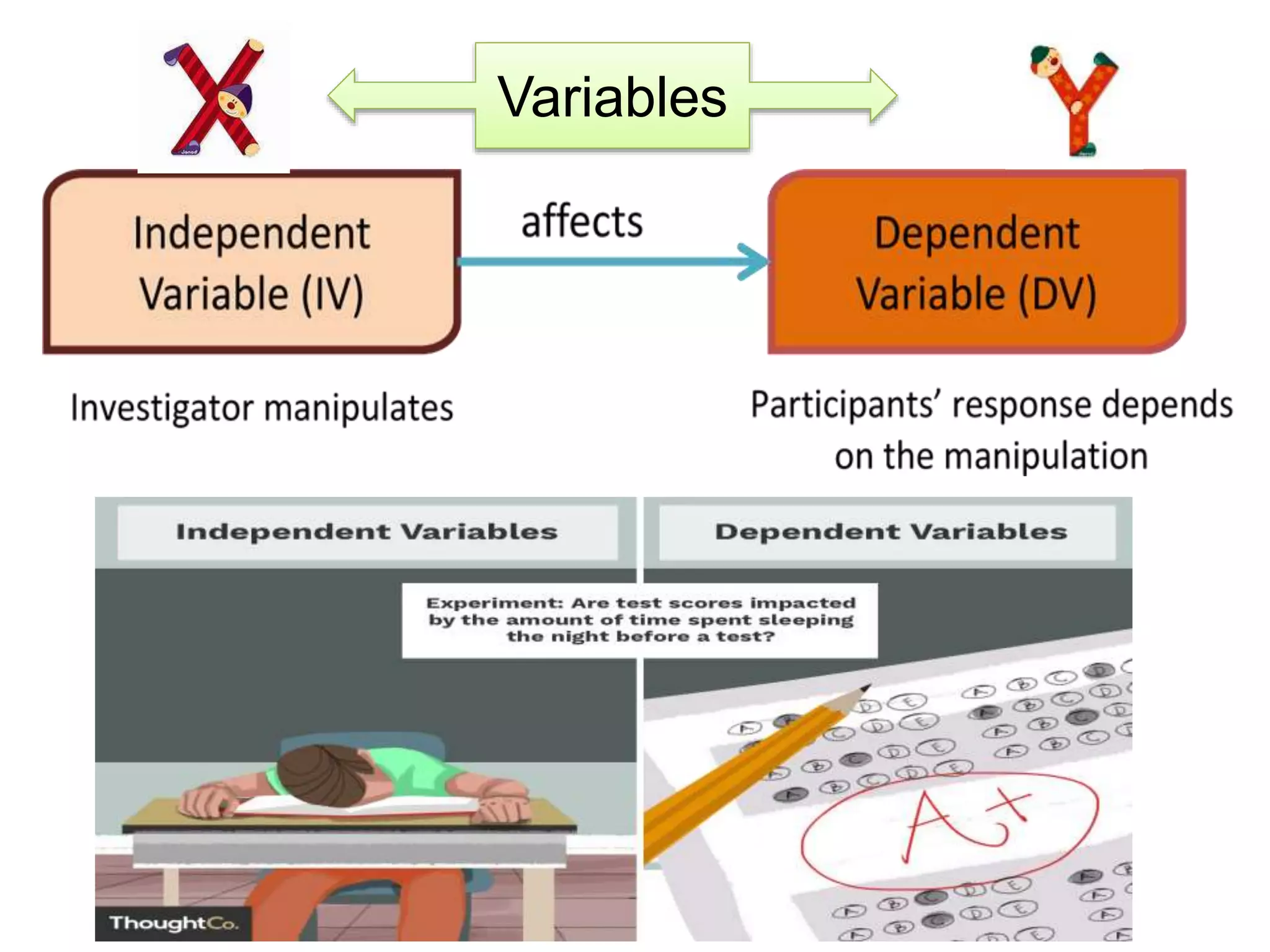
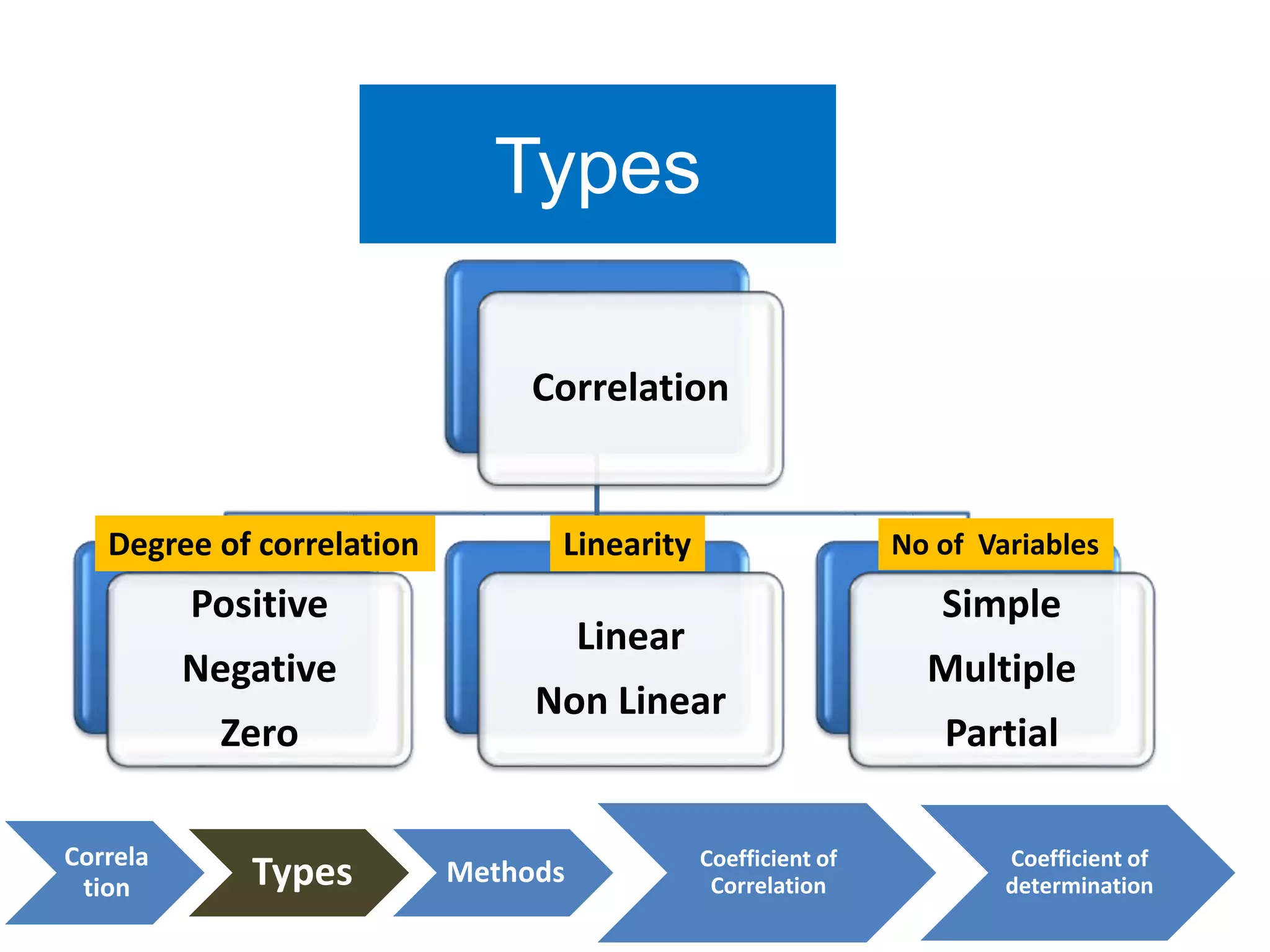
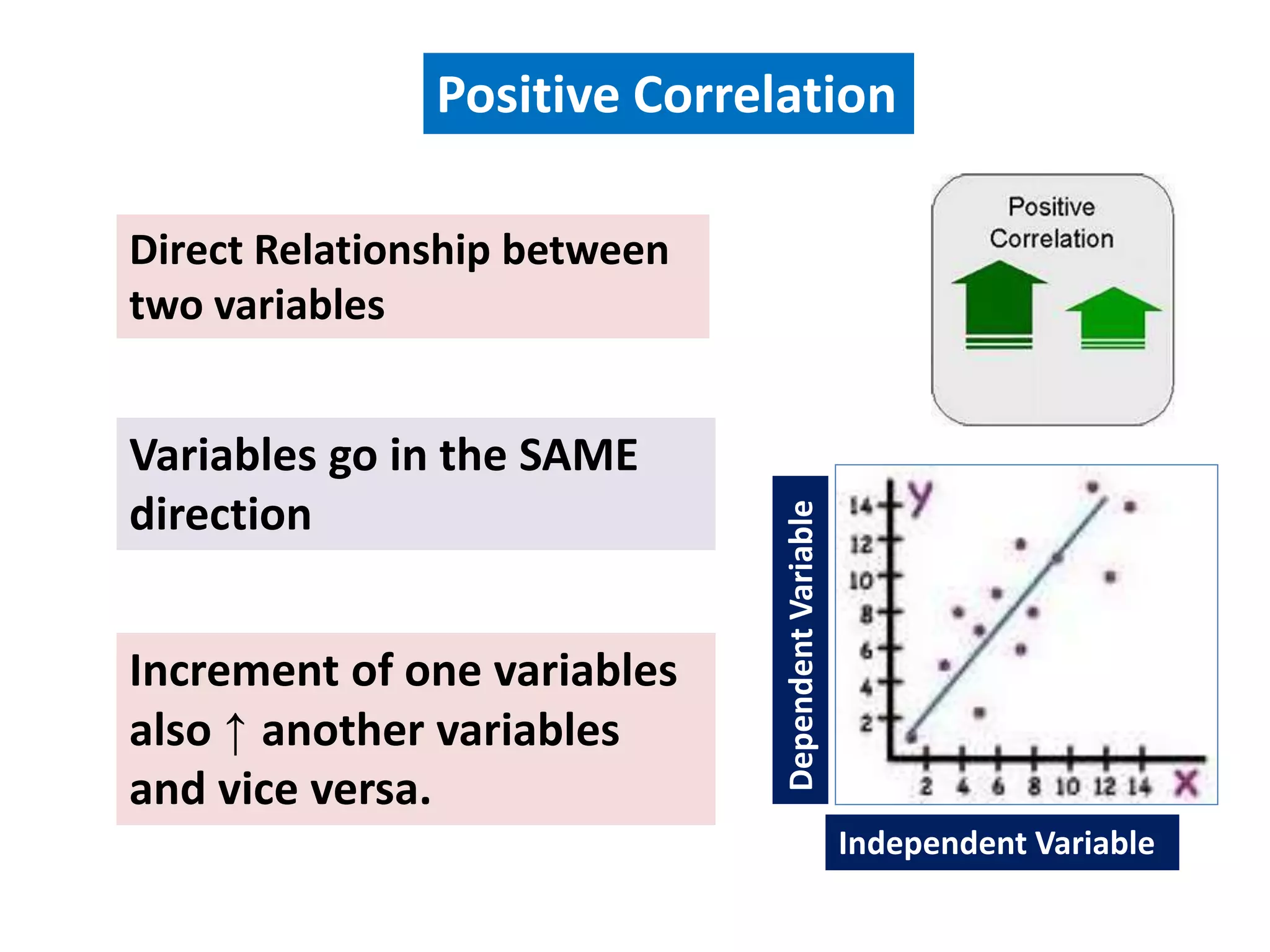
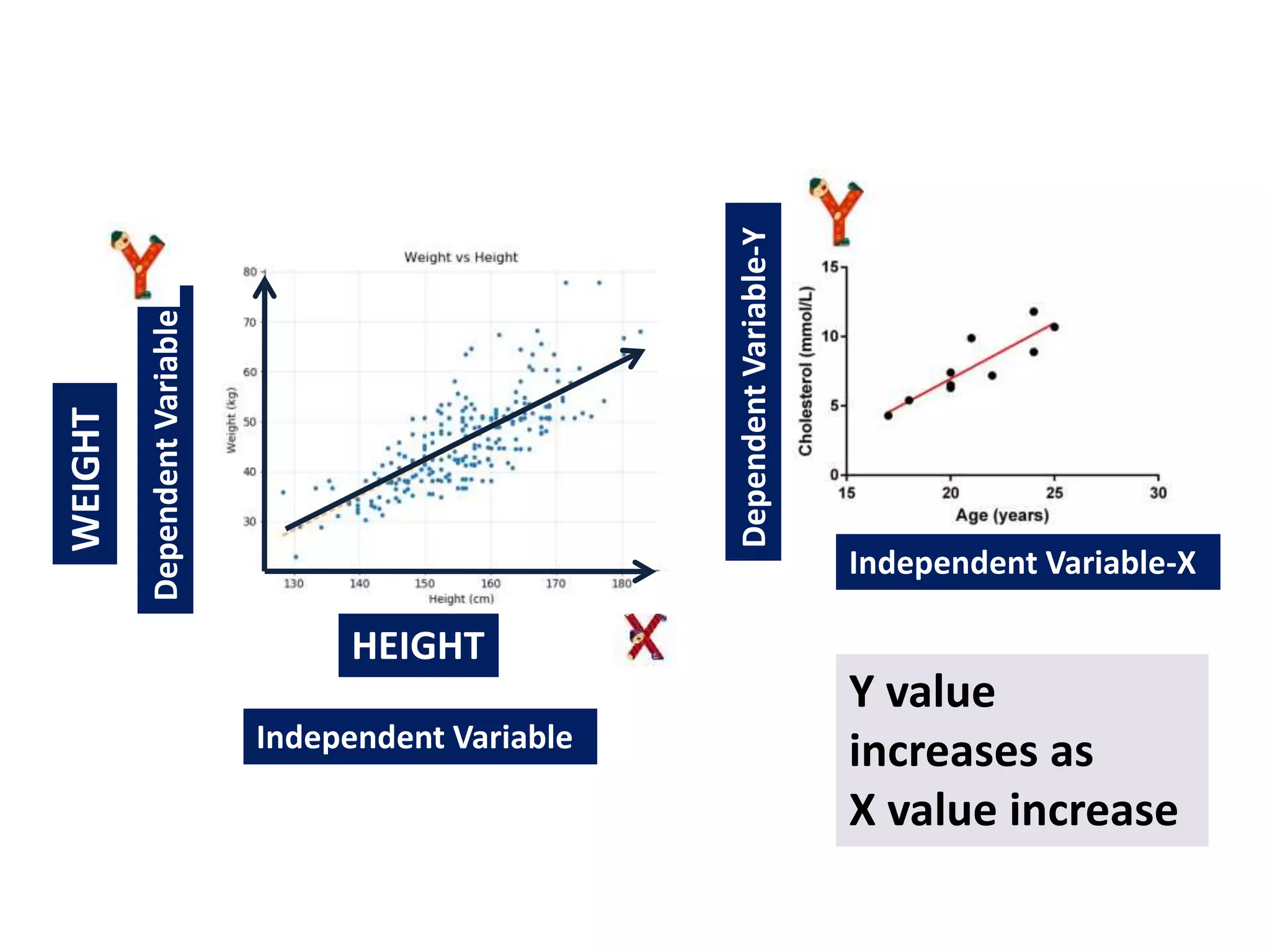
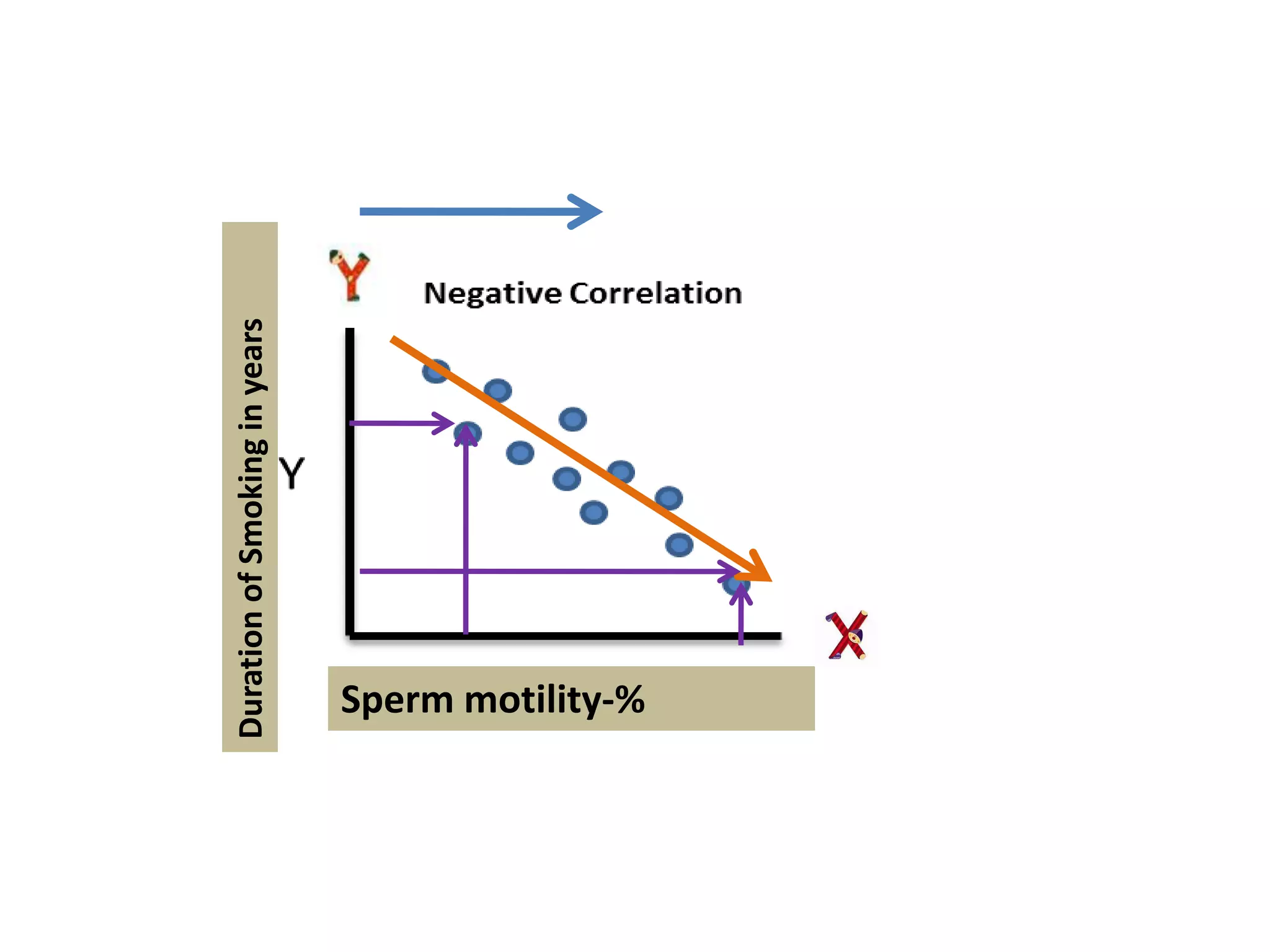
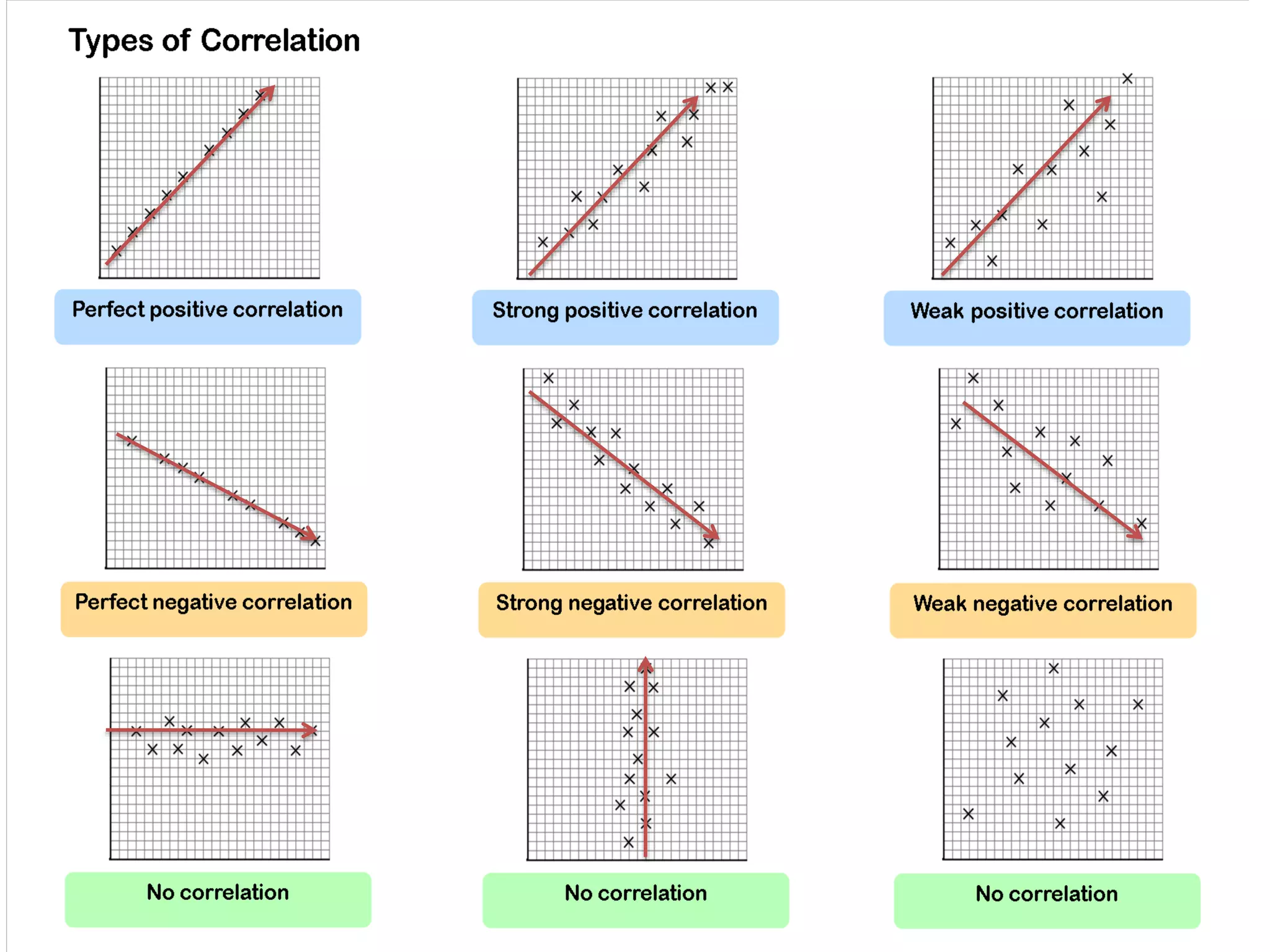
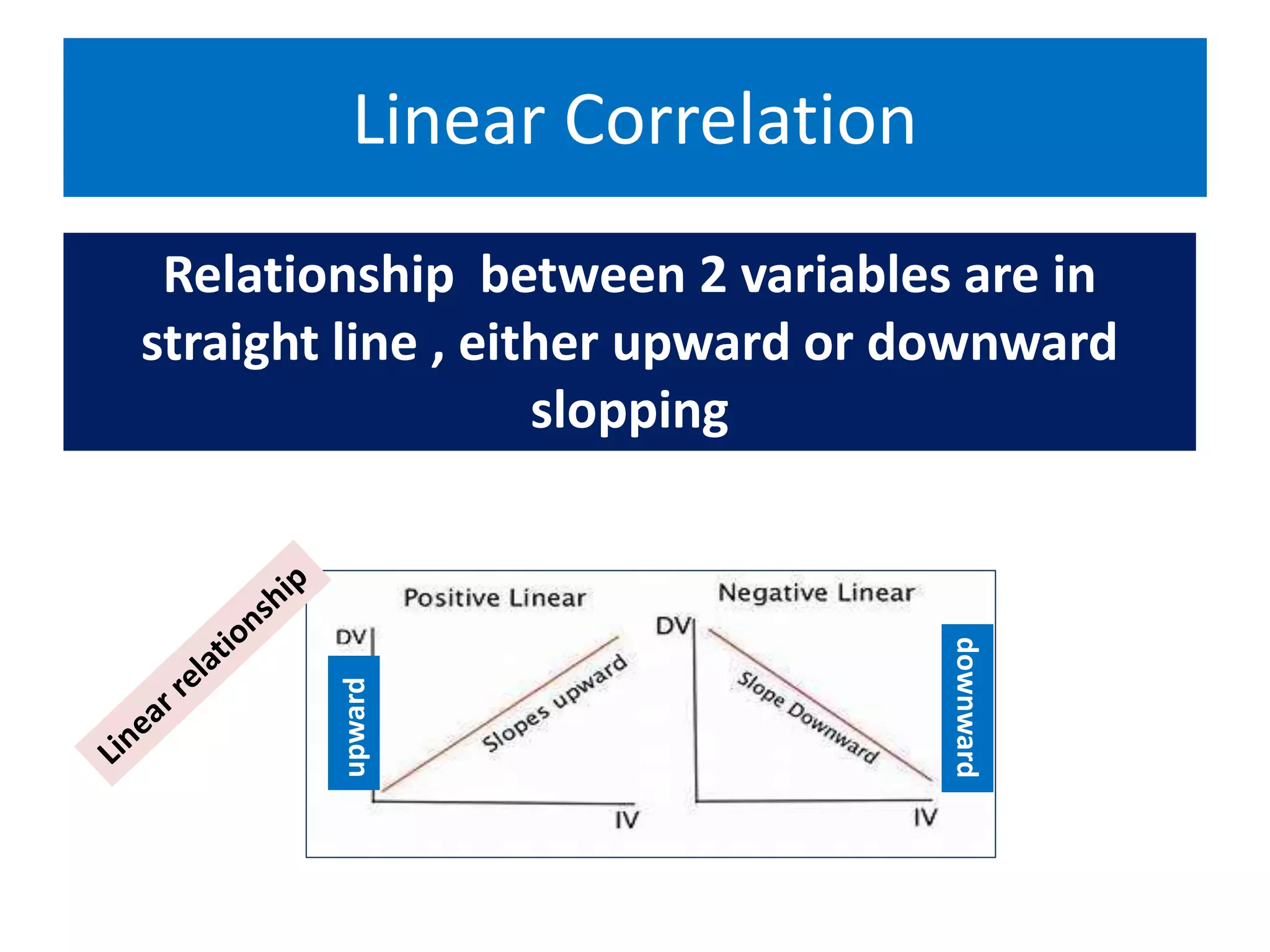
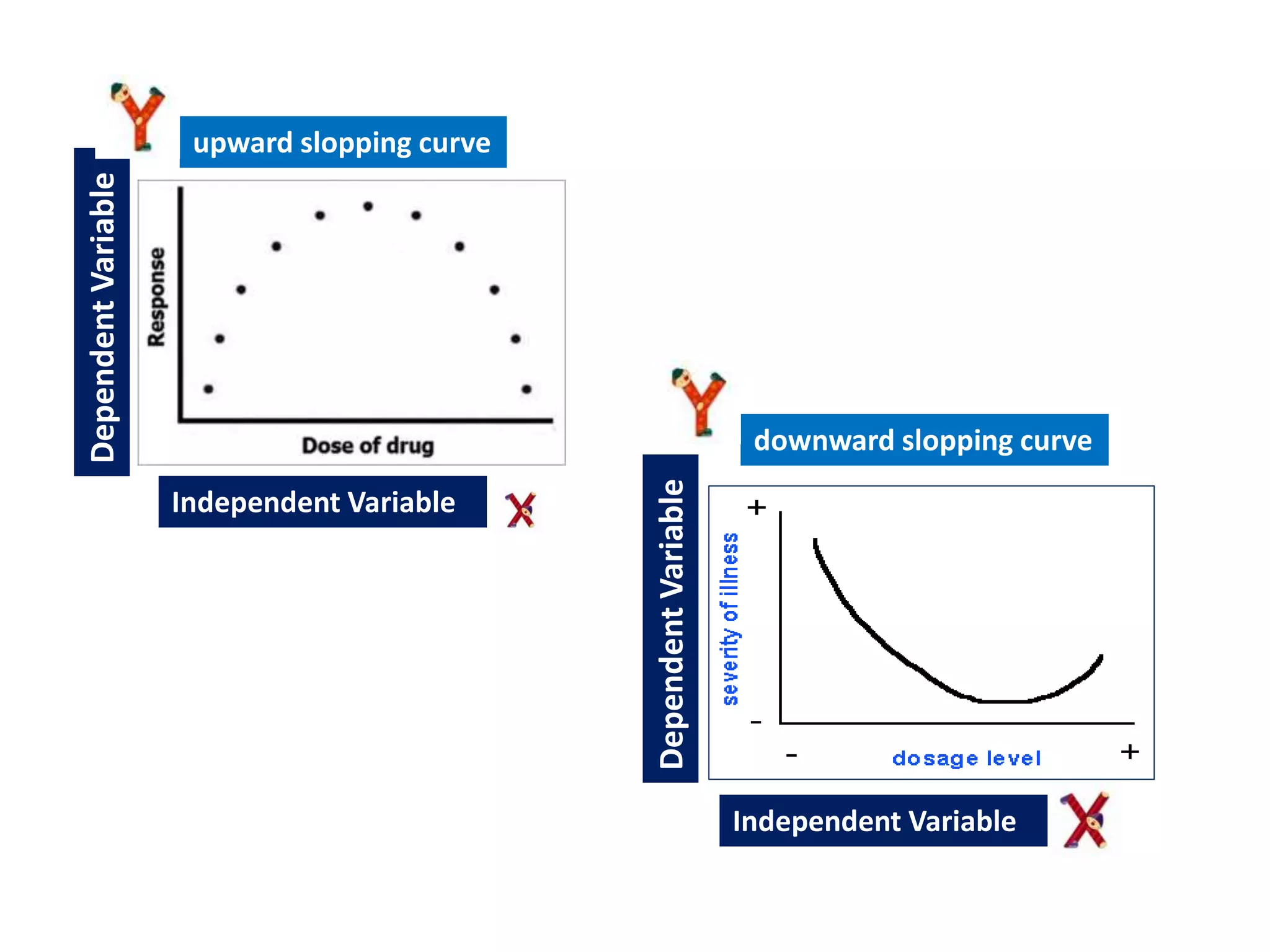
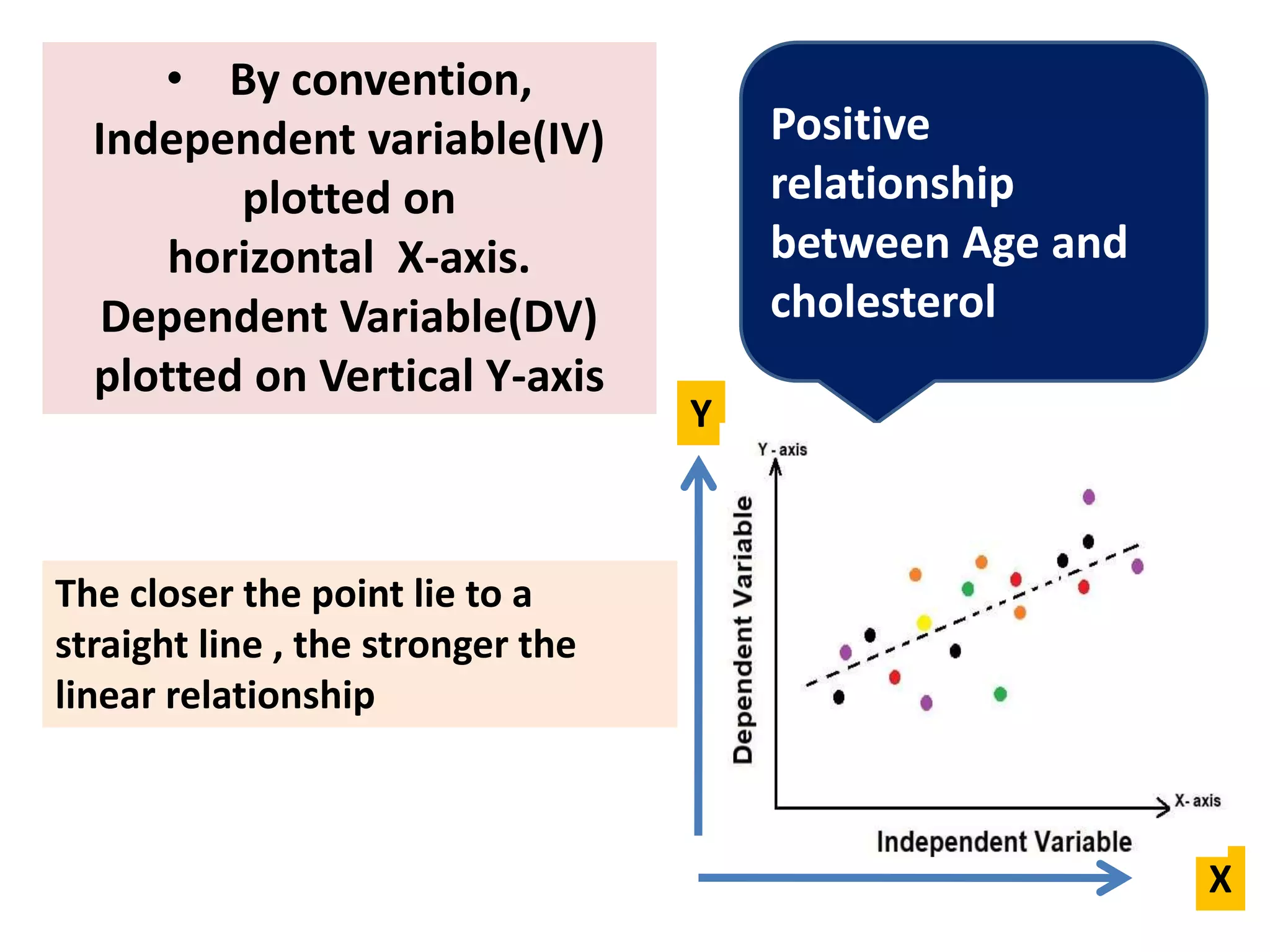
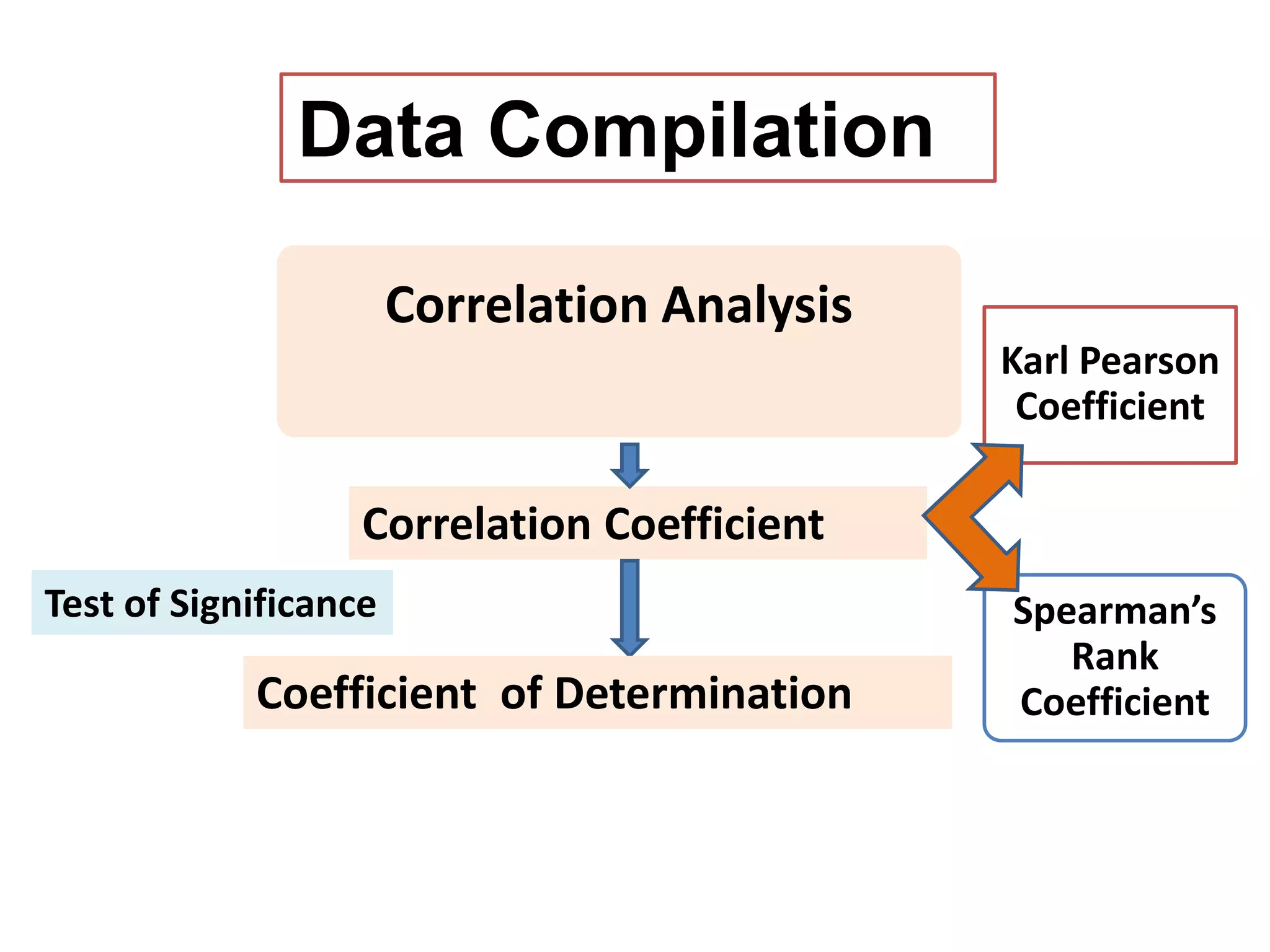
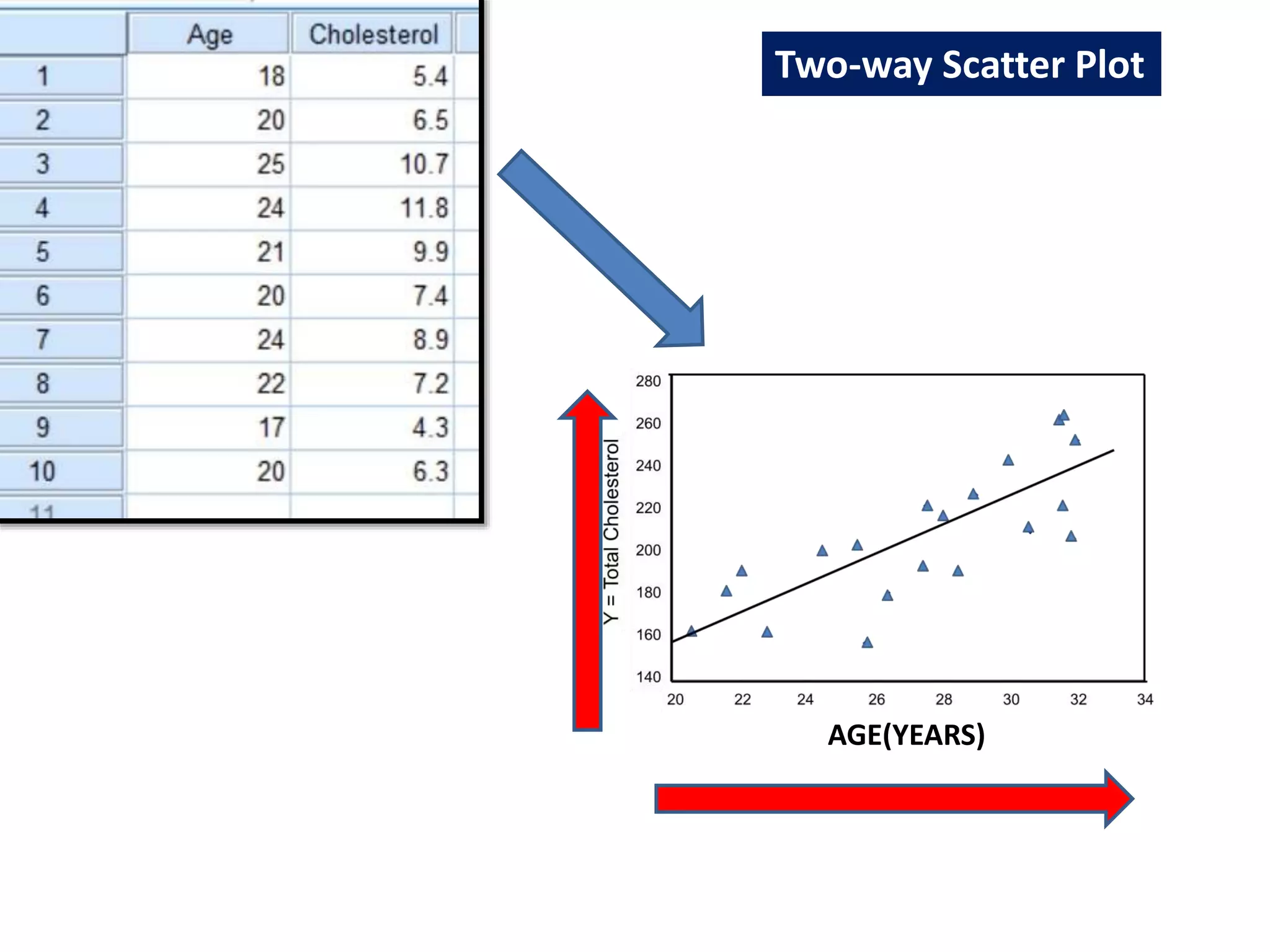
This document provides an overview of correlation, including: - Definitions of correlation and the concept of correlation being introduced in 1888. - The different types of correlation (positive, negative, zero, linear, non-linear, simple, multiple, partial). - Methods of studying correlation including graphic (scatter plots) and algebraic (correlation coefficients). - Karl Pearson's correlation coefficient and Spearman's rank correlation coefficient as measures of the strength and direction of linear relationships between variables. - The coefficient of determination which explains the percentage of variation in one variable explained by the other. 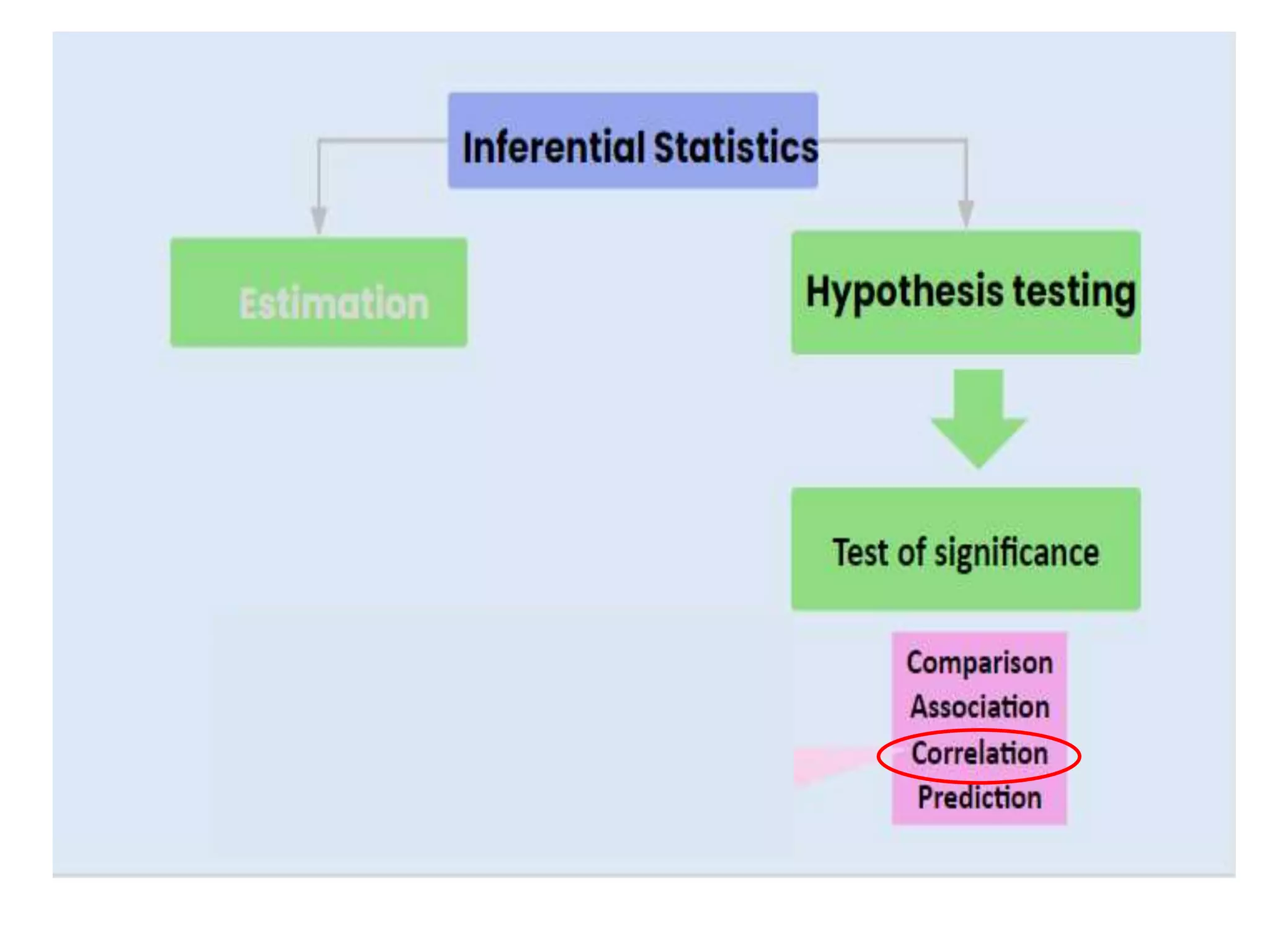- The importance of correlation analysis in determining relationships between variables and reducing uncertainty. - That correlation indicates association

1. CORRELATION
Fahmida Rashid Swati
Assistant Professor
Department of Obstetrics & Gynecology
Chittagong Medical College
Email:dr.fahmidaswati@gmail.com

2. X Y
সবুজ
Independent Dependant

3. Independent
Variables
Dependent
Variable

4. 1st 3rd
2nd
Rank
Independent
Variables
Dependent Variable

5. Quantity
Independent
Variables
Dependent Variable

6. Correlating efficacy and immunogenicity in
malaria vaccine trials.
Correlation of Maternal Age with
Prevalence of Chromosomal
Anomalies
Correlation of non-clinical parameters with
the hematological indices in type 2 diabetic
Mellitus patients
Correlation between Antibiotic
Consumption and Resistance of
Invasive Streptococcus in SSI.

7. Correlation

10. CORRELATION

11. History
1888-Francis Galton
concept of correlation.
kerl Pearson -1896
Reformulated
Correlation coefficient ’ r’
British Physiologist
E. E. Spearman in 1904,
Rank Correlation

12. Contents
Correla
tion Types Methods Coefficient of
Correlation
Coefficient of
determination

13. • Association or relationship between two
variables that don’t cause each other.
Correlation
The concept of
Correlation
X
Co vary --- Go Together
Y
Correla
tion Types Methods Coefficient of
Correlation
Coefficient of
determination

14. Variables

15. Purpose of Correlation
Determines values of one variable are
related to another or not
Y
X

16. Independent
Variables
Dependent
Variables
Grade
depends on
Number of Study Hour
Are these two
variables Related ?

17. Types
Correlation
Positive
Negative
Zero
Linear
Non Linear
Simple
Multiple
Partial
Degree of correlation No of Variables
Linearity
Correla
tion Types Methods Coefficient of
Correlation
Coefficient of
determination

18. Types
Correlation
Positive
Negative
Zero
Linear
Non Linear
Simple
Multiple
Partial
Degree of correlation No of Variables
Linearity
Correla
tion Types Methods Coefficient of
Correlation
Coefficient of
determination

19. Positive
Correlation

20. Positive Correlation
Variables go in the SAME
direction
Direct Relationship between
two variables
Increment of one variables
also ↑ another variables
and vice versa. Dependent
Variable
Independent Variable

21. HEIGHT
WEIGHT
Y value
increases as
X value increase
Independent Variable
Dependent
Variable
Dependent
Variable-Y
Independent Variable-X

22. Labor pain in hour- X axis
Dilatation
of
Cervix
Y-Axis
Independent Variable
Dependent
Variable
x
x
x

23. Negative
Correlation

24. Negative Correlation
Two Variable , X and Y go
In OPPOSITE direction
The ↑ in one variable X
results in the
corresponding ↓ in the
other variables.
Dependent
Variable
Independent Variable

25. Sperm motility-%
Duration
of
Smoking
in
years

26. Zero

27. Zero
• No correlation
Change of X
not associated with
change of Y
X
Y

29. Linear Correlation
Relationship between 2 variables are in
straight line , either upward or downward
slopping
upward
downward

30. Non Linear/Curvilinear
Ratio of changes between two
variables -not constant
• Relationship not in straight line,
• Either upward or downward slopping curve.

31. upward slopping curve
downward slopping curve
Dependent
Variable
Dependent
Variable
Independent Variable
Independent Variable

32. Partial
• Relationship between 2 variables keeping the
other variable constant or fixed
Influence of 3rd variable
Eliminated here.

33. Taking out the effect
of economic state
Mother Child

35. Multiple
• The relationship among 3 or more variables at
the same time.
Fetal Growth
Nutrition
Preeclampsia
Smoking

36. Collect
Data
Compile data
Method of
Studying
Correlation
Graphic
Algebraic
Correlation
Graph
Karl Pearson
Coefficient
Scattered
Diagram
Spearman’s
Rank
Coefficient

37. For this example
Null hypothesis is:
There is no correlation between participant ages
and blood total cholesterol levels.
Alternative hypothesis :
There is a correlation between participant ages
and blood total cholesterol levels.

39. Graphic

40. AGE(YEARS)

41. Scattered Diagram Method
Each points of Graph
represents a
combination value - Xi
& Yi
One of the simplest ways of diagrammatic
representation of the quantitative bi-variate.
cholesterol
age
Dependent
Variable
Independent Variable
Cholesterol

42. Positive
relationship
between Age and
cholesterol
• By convention,
Independent variable(IV)
plotted on
horizontal X-axis.
Dependent Variable(DV)
plotted on Vertical Y-axis
X
Y
The closer the point lie to a
straight line , the stronger the
linear relationship

43. Two information
• Nature &
Strength
Pattern of
Relationship

44. Advantage:
•First Steps in investigating relationship between
two variables.
•Simple & Non mathematical
Disadvantage:
Can not adopt an exact degree of
correlation
Existence of linear relationship between X & Y
determined Via scatter Plot

45. Data Compilation
Correlation Analysis
Correlation Coefficient
Karl Pearson
Coefficient
Spearman’s
Rank
Coefficient
Coefficient of Determination
Test of Significance

46. Examining the relationship between two
variables systematically
Correlation analysis

47. AGE(YEARS)
Two-way Scatter Plot

48. A measure of the strength & direction of a linear
relationship between two variables.
Correlation Coefficient
Strength Direction
values closer to -1
or +1 indicate
greater strength -ive -
inverse
/indirect
relation
+ive
same
direction/
direct relation

49. Correlation Coefficient
Computed from sample data
‘r’
p (rho)
‘r’ has no unit

50. Within SPSS, go to Analyze > Correlate >
Bivariate.

51. Association Between
Height & Weight
Association between
Hb% with Socio-
economic status
Two continuous Variables
Pearson
One continuous and One
categorical
Variable(Ordinal)/Ranked
order scale
Spearman
Decide And Calculate Correlation Coefficient:

52. Most
Popular
Normally
distributed
linear
relationship
Quantitative
variable

53. Gives precise numerical value of degree of
linear relationship between two variable.
‘r’- value has nothing to do with 90% CI

54. Non parametric
Represent paired observations
Assumptions of the Pearson
correlation are markedly violated

55. • ‘r’ and rs similar Meaning
• Difference is :

56. A new window will open called Bi-variate Correlations.
Here, specify which variables want to include in the
analysis.
Ensure that Pearson is ticked under the
title Correlation Coefficients
Since prior assumptions was not made,
tick -Test of Significance as
Two-tailed
Click
Here

57. Output:
By going to the SPSS Output window, there will be a
new heading of Correlations with a correlation matrix
displayed
This is the Pearson Correlation
Coefficient (r) value
The P value for a two-
tailed analysis
N – The number of pairs of data in the
analysis.

58. r= +1= Perfect +ive linear
relationship
Range of Correlation Coefficient
-1 to +1
r= -1=Perfect -ive linear
relationship

59. Interpretation of Value of ‘r’
Larger absolute value of r – stronger relationship

61. Interpretation
By looking at the results, it can be seen that the
correlation between age and blood
cholesterol levels gave a r value of 0.882,
which indicates a strong positive correlation
between the two variables.
Also, the P value of the association was 0.001, thus
indicating a highly significant result.
Therefore, I will reject
the null hypothesis.

62. Reporting

63. Importance of Correlation analysis
Used to derive degree/strength & direction of
relationship between 2 variables.
Useful in presenting average relationship between
2 variables.
Use to ↓ range of uncertainty in matter of
prediction.

65. Coefficient of Determination(CoD)
Used for interpretation of correlation &
comparing 2 or More correlation coefficient
Square of Correlation Coefficient
Explain % of variation in Y that can be explained
in terms of X.
r2

66. If r=0.8 , r2= 0.64
It implies that 64% of total variations in Y occurs
due to X.
The remaining 34% variation occurs due to external
factors.
How strong is relationship
between Predictor &
Outcome.

67. If Pearson r = -0.5 r2= 0.25
Expression:
25% of variability in GPA scores accounted by depression
(remaining 75% of variability is other factors, habits,
ability, motivation, courses studied , etc)
Correlation of Depression with GPA grade:

68. If ‘r’ = 0.5 r2 = 0.25
If ‘r’ = 0.7 r2 = 0.49
r2 tells us that -
r = 0.7 accounts for about 2 fold
variability relative to r= 0.5
While ‘r’ = 0.5 Vs 0.7
might not look so different in terms of
strength.
0.49
0.25

70. Causation:
Cause & Effect Relation
Correlation :
•Interdependency among
Variables for correlating 2
phenomenon.
Two variables vary in such
away that movement in one
accompanied by movement in
other.
Causation always implies
correlation
but
correlation does not
necessarily implies causation.

71. With large sample , even a small correlation can be
statistically significant
Correlation measure association not causation.
Correlation assumes linear relationship.
Take Home Massage :
Statistically significant correlation may not be practically
significant.

72. Values between -1 & +1
Measure strength & direction of the relationship
In simple linear Correlation Coefficient – variables
normally distributed.
In Spearman’s Rank Correlation Coefficient – variables
doesn’t follow normal distribution.

73. Choosing the
‘right Method’ for the data
is the key statistical expertise one
need to have .

74. CMCTA