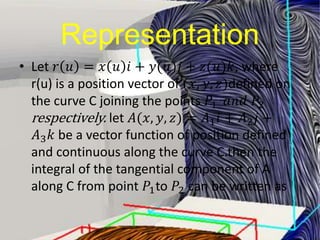
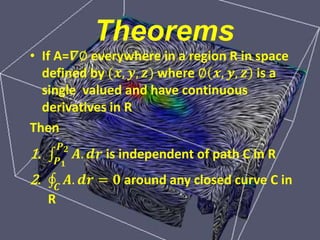
This document defines and explains line integrals. It defines a line integral as the integral of a function along a line or curve, where the function has a continuously varying value along that line. It discusses how line integrals were developed to solve problems involving fluid flow, forces, electricity, and magnetism. It provides representations of line integrals using vector notation and explains that if the vector field is conservative, the line integral is path independent and can be written as the difference of a potential function between two points.

1. Presented By
• Tayyaba Abbas (05)
• Muhammad Ahmad Khan (24)
• Muhammad Farhan Hussain (19)
• Pakeeza jabeen (14)

2. Line integral

3. What is line integral
the integral, taken
along a line, of any
function that has a
continuously varying value
along that line.

4. History
• They were invented in the
early 19th century to solve
problems involving:
Fluid flow
Forces
Electricity
Magnetism

5. Representation
• Let 𝑟 𝑢 = 𝑥 𝑢 𝑖 + 𝑦(𝑢)𝑗 + 𝑧(𝑢)𝑘, where
r(u) is a position vector of (𝑥, 𝑦, 𝑧)defined on
the curve C joining the points 𝑃1 𝑎𝑛𝑑 𝑃2
respectively. let 𝐴(𝑥, 𝑦, 𝑧) = 𝐴1 𝑖 + 𝐴2 𝑗 +
𝐴3 𝑘 be a vector function of position defined
and continuous along the curve C.then the
integral of the tangential component of A
along C from point 𝑃1to 𝑃2 can be written as

6. 𝑃1
𝑃2
𝐴. 𝑑𝑟 =
𝐶
𝐴. 𝑑𝑟 = 𝐶
𝐴1 𝑑𝑥 + 𝐴2 𝑑𝑦 + 𝐴3 𝑑𝑧

7. Note
• If A is the force F on the particle move along
the curve then the line integral is called Work
done.
• In Aerodynamic or fluid mechanics this
integral is called circulation of A along the
curve C , where A represents the velocity of
the fluid

8. Note
• In general line integral is that which is to be
evaluated along the curve. Such integrals are
defined in terms of sum of limits as integrals
of calculus

9. Theorems
• If A=𝜵∅ everywhere in a region R in space
defined by (𝒙, 𝒚, 𝒛) where ∅ 𝒙, 𝒚, 𝒛 is a
single valued and have continuous
derivatives in R
Then
1. 𝑷 𝟏
𝑷 𝟐
𝑨. 𝒅𝒓 is independent of path C in R
2. 𝑪
𝑨. 𝒅𝒓 = 𝟎 around any closed curve C in
R

10. A is conservative when 𝛁 × 𝑨 = 𝟎 𝒐𝒓𝑨 =
𝛁∅𝒊𝒏 𝒔𝒖𝒄𝒉 𝒄𝒂𝒔𝒆𝒔 𝑨. 𝒅𝒓 =
𝒅∅ 𝒆𝒙𝒂𝒄𝒕 𝒅𝒊𝒇𝒇𝒆𝒓𝒆𝒏𝒕𝒊𝒂𝒍
In such case A is called a
conservative field and ∅ is scalar
potential .

11. Conservative vector
field
Conservative vector fields have the
property that the line integral from one
point to another is independent of the
choice of path connecting the two points: it
is path independent. Conversely, path
independence is equivalent to the vector
field being conservative.

12. Role of line integrals in
vector calculus
• The line integral of a vector field plays a crucial role in vector
calculus. Out of the four fundamental theorems of vector
calculus, three of them involve line integrals of vector
fields. Green's theorem and Stokes' theorem relate line
integrals around closed curves to double integrals or surface
integrals. If you have a conservative vector field, you
can relate the line integral over a curve to quantities just at
the curve's two boundary points. It's worth the effort to
develop a good understanding of line integrals.

13. Example Questions