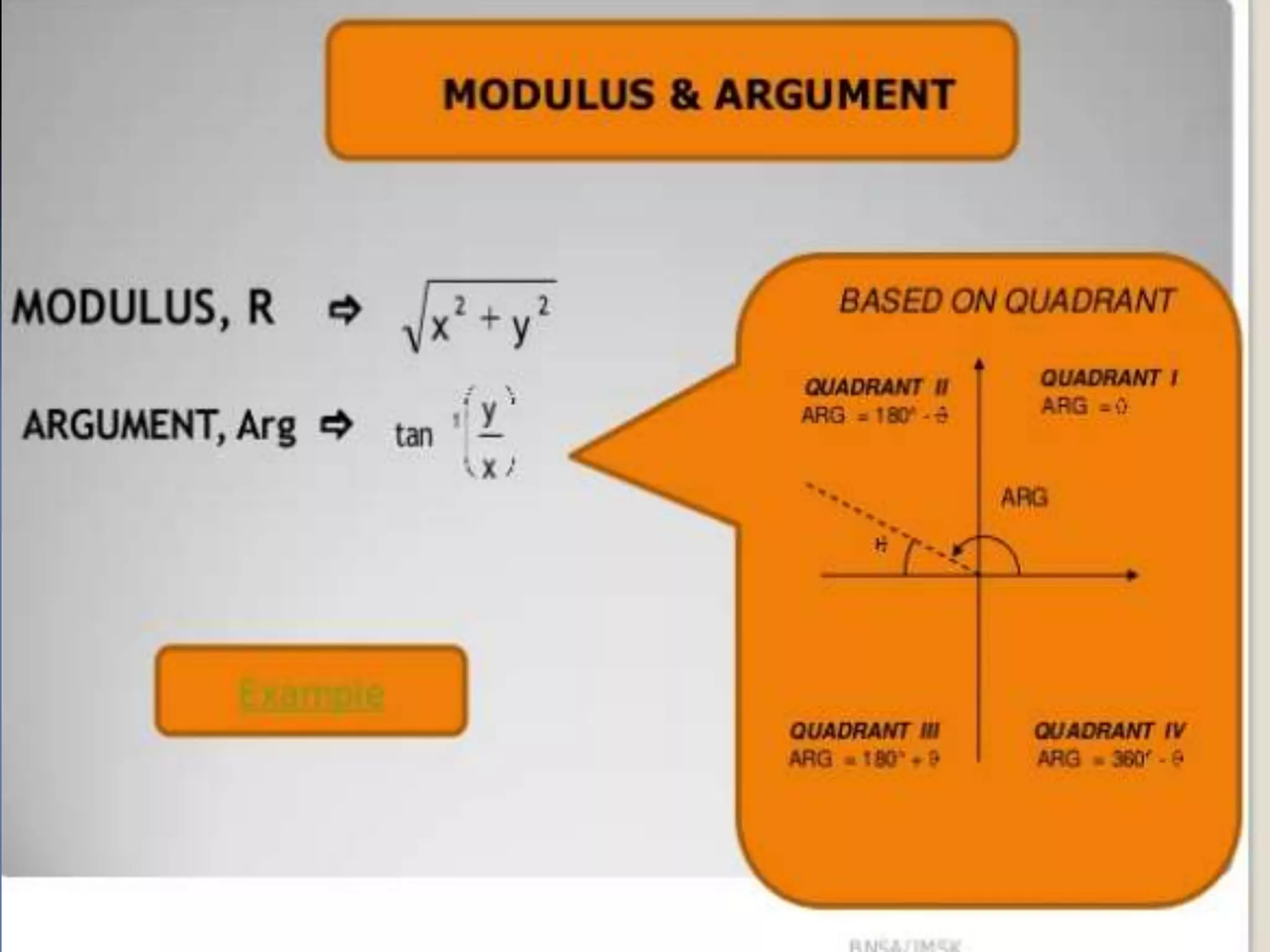
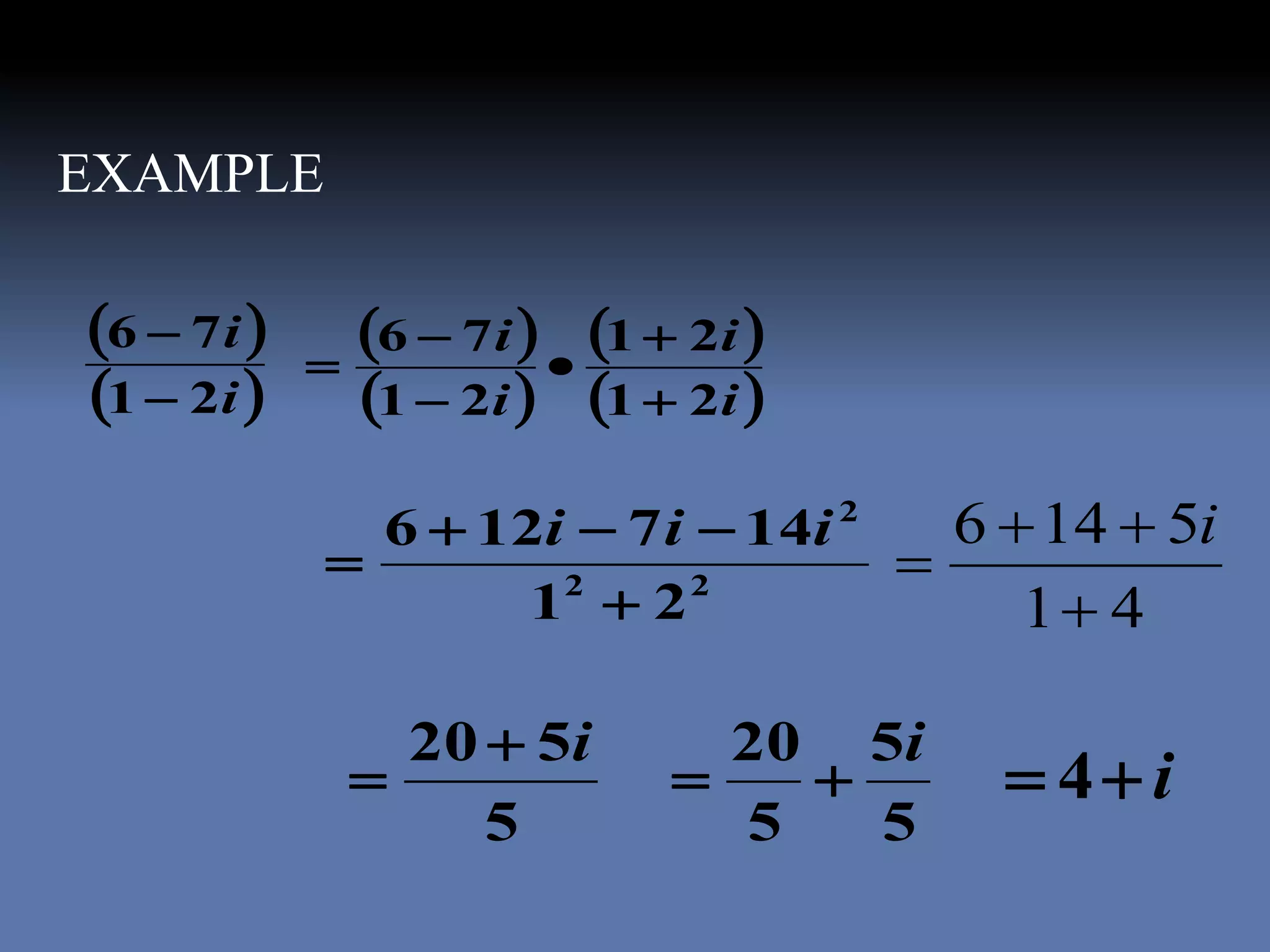This document contains information about Md. Arifuzzaman, a lecturer in the Department of Natural Sciences at the Faculty of Science and Information Technology, Daffodil International University. It includes his employee ID, designation, department, faculty, personal webpage, email, and phone number. The document also provides an overview of complex numbers, including their history, the number system, definitions of complex numbers, operations like addition and multiplication of complex numbers, and applications of complex numbers.

2. Name :
Md. Arifuzzaman
Employee ID
710001113
Designation
Lecturer
Department
Department of Natural Sciences
Faculty
Faculty of Science and Information Technology
Personal Webpage
http://faculty.daffodilvarsity.edu.bd/profile/ns/arifuzzaman.ht
ml
E-mail
zaman.ns@daffodilvarsity.edu.bd
Phone
Cell-Phone
+8801725431992

5.  History.
 Number System.
 Complex numbers.
 Operations.
5(Complex Number)
Contents

6.  Complex numbers were first introduced by G.
Cardano
 R. Bombelli introduced the symbol 𝑖.
 A. Girard called “solutions impossible”.
 C. F. Gauss called “complex number”
6(Complex Number)
History

7. 7(Complex Number)
Number System
Real
Number
Irrational
Number
Rational
Number
Natural
Number
Whole
Number
Integer
Imaginary
Numbers

8. 8(Complex Number)
Complex Numbers
• A complex number is a number that can b express in
the form of "a+b𝒊".
• Where a and b are real number and 𝑖 is an imaginary.
• In this expression, a is the real part and b is the
imaginary part of complex number.

9. Complex Number
Real
Number
Imaginary
Number
Complex
Number
When we combine the real and
imaginary number then
complex number is form.

10. 10(Complex Number)
Complex Number
• A complex number has a real part and an imaginary part,
But either part can be 0 .
• So, all real number and Imaginary number are also
complex number.

11. 11(Complex Number)
Complex Numbers
Complex number convert our visualization into physical things.

12. A complex number is a number consisting
of a Real and Imaginary part.
It can be written in the form
COMPLEX NUMBERS
1i

13. COMPLEX NUMBERS
 Why complex numbers are introduced???
Equations like x2=-1 do not have a solution within
the real numbers
12
x
1x
1i
12
i

14. COMPLEX CONJUGATE
 The COMPLEX CONJUGATE of a complex number
z = x + iy, denoted by z* , is given by
z* = x – iy
 The Modulus or absolute value
is defined by
22
yxz 

15. COMPLEX NUMBERS
Equal complex numbers
Two complex numbers are equal if their
real parts are equal and their imaginary
parts are equal.
If a + bi = c + di,
then a = c and b = d

16. idbcadicbia )()()()( 
ADDITION OF COMPLEX NUMBERS
i
ii
)53()12(
)51()32(


i83 
EXAMPLE
Real Axis
Imaginary Axis
1z
2z
2z
sumz

17. SUBTRACTION OF COMPLEX
NUMBERS
idbcadicbia )()()()( 
i
i
ii
21
)53()12(
)51()32(



Example
Real Axis
Imaginary Axis
1z
2z
 2z
diffz
 2z

18. MULTIPLICATION OF COMPLEX
NUMBERS
ibcadbdacdicbia )()())(( 
i
i
ii
1313
)310()152(
)51)(32(



Example

19. DIVISION OFACOMPLEX
NUMBERS
 
 dic
bia

  
 
 
 dic
dic
dic
bia






22
2
dc
bdibciadiac



 
22
dc
iadbcbdac




20. EXAMPLE
 
 i
i
21
76

  
 
 
 i
i
i
i
21
21
21
76






22
2
21
147126



iii
41
5146



i
5
520 i

5
5
5
20 i
 i 4

21. DE MOIVRE'S THEORoM
DE MOIVRE'S THEORM is the theorm which show us
how to take complex number to any power easily.

22. Euler Formula


j
re
jyxjrz

 )sin(cos
 yjye
eeee
jyxz
x
jyxjyxz
sincos 



This leads to the complex exponential
function :
The polar form of a complex number can be rewritten as

23. So any complex number, x + iy,
can be written in
polar form:
Expressing Complex Number
in Polar Form
sinry cosrx 
irryix  sincos 

24. A complex number, z = 1 - j
has a magnitude
2)11(|| 22
z
Example
rad2
4
2
1
1
tan 1











 
 


 nnzand argument :
Hence its principal argument is : rad
Hence in polar form :
4

zArg








4
sin
4
cos22 4


jez
j

25. EXPRESSING COMPLEX NUMBERS IN POLAR FORM
x = r cos 0 y = r sin 0
Z = r ( cos 0 + i sin 0 )

28. APPLICATIONS
 Complex numbers has a wide range of
applications in Science, Engineering,
Statistics etc.
Applied mathematics
Solving diff eqs with function of complex roots
Cauchy's integral formula
Calculus of residues
In Electric circuits
to solve electric circuits

29.  Examples of the application of complex numbers:
1) Electric field and magnetic field.
2) Application in ohms law.
3) In the root locus method, it is especially important
whether the poles and zeros are in the left or right
half planes
4) A complex number could be used to represent the
position of an object in a two dimensional plane,
How complex numbers can be applied to
“The Real World”???

30. REFERENCES..
 Wikipedia.com
 Howstuffworks.com
 Advanced Engineering
Mathematics
 Complex Analysis