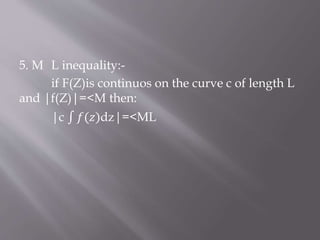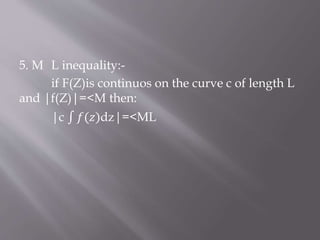
The document discusses line integrals of complex functions along curves. It defines a line integral as the integral of a continuous function f(z) along a curve c from point A to B, which is divided into n parts. It also provides the definition of a line integral in terms of a parameterization z(t) of the curve from a to b. Finally, it lists five properties of line integrals: linearity, sense reversal, partitioning of paths, integral inequality, and the Mean Value inequality.

1. 140410119100 - Jay Rami
140410119101 - Malhar Rana
140410119102 –Raval Harsh
140410119103 – Raval Parth
140410119104 – Ray Bhargav

2.  Let f(z)be a continuous function of the complex
variable z=x+iy defined at every point of a
curve c whose end points are A and B divide
the curve c into n parts at the points
 A=P0(z0),P1(z1)……..Pn(zn)=B
 Line integral of f(z) along the path C and is
denoted by 𝑓(𝑧) dz if c is a closed curve.

4. Suppose that the equation z=z(t) represents the
contour c from point z=a to z=b also f(z) is
piecewise continuous on c then line integral or
contour integral of f along c in terms of
parameter of t is : c 𝑓(𝑧) dz = 𝑓(𝑧(𝑡)).z’(t)dt
Provided z’(t) is piecewise continuous.

5.  PROPERTIES OF LINE INTEGRALS:-
If F(z) and G(z) are integrable along a curve C
then the following properties hold:
1. Linearity
2. Sense reversal
3. Partitioning of path
4. Integral inequality
5. ML inequality

6. 1. Linearity:-
c [ 𝑘1𝑓(𝑧)+k2 G(z)]dz=k1 c 𝑓(𝑧) dz +k2 c 𝐺(𝑧)dz
For example:

7. 2. Sense reversal:-
𝑎
𝑏
𝑓(𝑧)dz=- 𝑏
𝑎
𝑓(𝑧) dz
3.Patitioning of path:-
if the curve C consists of the curve c1 and c2
then:
𝑐 𝑓(𝑧) dz = c1 𝑓(𝑧)dz+c2 𝑓(𝑧)dz
4. Integral inequality:
|c 𝑓(𝑧)dz|=< c |𝑓(𝑧) ||dz|

10. 5. M L inequality:-
if F(Z)is continuos on the curve c of length L
and |f(Z)|=<M then:
|c 𝑓(𝑧)dz|=<ML