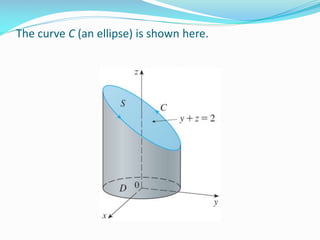
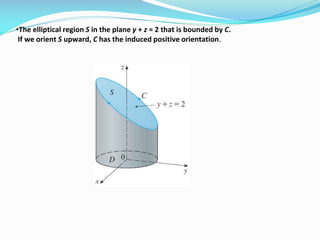
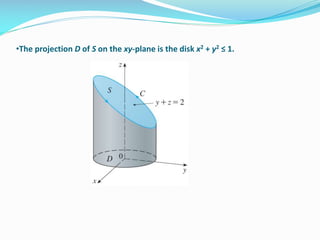
1) Stokes' theorem relates a surface integral over a surface S to a line integral around the boundary curve of S. It states that the line integral of a vector field F around a closed curve C that forms the boundary of a surface S is equal to the surface integral of the curl of F over the surface S. 2) In Example 1, Stokes' theorem is used to evaluate a line integral around an elliptical curve C by calculating the corresponding surface integral over the elliptical region S bounded by C. 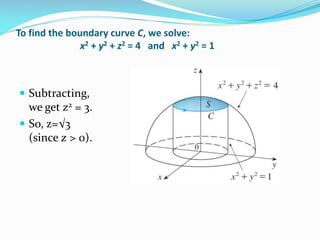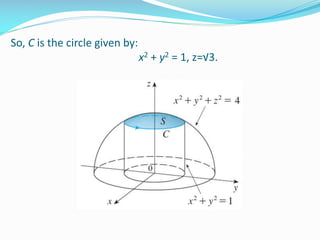3) In Example 2, Stokes' theorem is again used, this time to evaluate a line integral around a circular curve C by calculating the surface integral over the part of a sphere bounded by C.

1. By:
Abhishek Singh Chauhan
Scholar no. 121116087

2. Let S be an open surface bounded by a closed curve C and vector F be any
vector point function having continuous first order partial derivatives. Then
C F. dr = ∫∫s curl F.ň ds
where ň= unit normal vector at any point of S drawn in the sense in which a right
handed screw would advance when rotated in the sense of the description of C.
Stokes’s Theorem relates a surface integral over
a surface S to a line integral around the boundary
curve of S (a space curve).
Statement:

3. Evaluate
∫c F.dr
where:
 F(x, y, z) = –y2 i + x j + z2 k
 C is the curve of intersection of the plane
y + z = 2 and the cylinder x2 + y2 = 1.
(Orient C to be counterclockwise
when viewed from above.)
Example 1

4. The curve C (an ellipse) is shown here.

5. We first compute:
 
2 2
curl 1 2y
x y z
y x z
  
  
  

i j k
F k

6. •The elliptical region S in the plane y + z = 2 that is bounded by C.
If we orient S upward, C has the induced positive orientation.

7. •The projection D of S on the xy-plane is the disk x2 + y2 ≤ 1.

8.  
 
 
 
2 1
0 0
12 3
2
0
0
2
1 2
2 30
1
2
curl 1 2
1 2 sin
2 sin
2 3
sin
2 0
C
S D
d d y dA
r r dr d
r r
d
d



 
 
 
 
    
 
 
  
 
 
  
  
 


F r F S

9. Use Stokes’ Theorem to compute ∫∫ curl F.ds
where:
 F(x, y, z) = xz i + yz j + xy k
 S is the part of
the sphere
x2 + y2 + z2 = 4
that lies inside
the cylinder
x2 + y2 =1
and above
the xy-plane.
Example 2

10. To find the boundary curve C, we solve:
x2 + y2 + z2 = 4 and x2 + y2 = 1
 Subtracting,
we get z2 = 3.
 So, z=√3
(since z > 0).

11. So, C is the circle given by:
x2 + y2 = 1, z=√3.

12. A vector equation of C is:
r(t) = cos t i + sin t j + √3k 0 ≤ t ≤ 2π
Therefore, r’(t) = –sin t i + cos t j
Also we have:
   3cos 3sin cos sint t t t t  F r i j k

13. Thus, by Stokes’ Theorem,
 
2
0
2
0
2
0
curl
( ( )) '( )
3cos sin 3sin cos
3 0 0
C
S
d d
t t dt
t t t t dt
dt



  
 
  
 
 



F S F r
F r r

14. Verify Stokes’ Theorem for the field F =<x2, 2x, z2> on the ellipse S = {(x, y , z) :
4x2 + y 2 6 4, z = 0}.
Solution: We compute both sides in ∫c F · dr =∫∫s curl F · n dσ.
We start computing the circulation
integral on the ellipse x2 + =1.
We need to choose a counterclockwise parametrization,
hence the normal to S
points upwards. We choose, for t ∈ [0, 2π],
r(t) = <cos(t), 2 sin(t), 0>.
Therefore, the right-hand rule normal n to S is n = <0, 0,
Example 3

15. Recall: ∫ c F · dr = ∫∫s curl F · n dσ. r(t) = <cos(t), 2 sin(t), 0>, t ∈ [0, 2π] and n = <0, 0,
1>. The circulation integral is:
∫ F. dr=
∫c F. dr=
The substitution on the first term u = cos(t) and du = − sin(t) dt implies
=
Since = 0, we conclude that ∫c F. dr= 4π

16. We now compute the right-hand side in Stokes’ Theorem.
I = ∫∫s curl F · n dσ.
Solving, we get: curl F=<0,0,2>.
S is the flat surface {x2 + <=1,z= 0} so dσ = dx dy.
Then,∫∫ (curl F).n dσ =
The right-hand side above is twice the area of the ellipse. Since we
know that an ellipse = 1 has area πab, we obtain
∫∫s curl F · n dσ= 4π.
This verifies Stokes’ Theorem.

17. Thank
you!!!!!