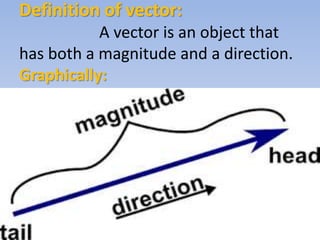
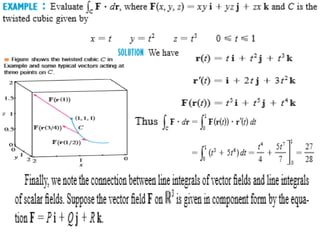
The document defines key concepts related to line integrals of vector fields. It defines a vector as having both magnitude and direction. It then defines a line integral as integrating a function along a line, and defines a vector field as a region where a vector quantity (like magnetic field) assigns a unique vector value to each point. Finally, it discusses the definition of a line integral of a vector field, and three fundamental theorems relating line integrals to other integrals: the gradient theorem relating it to differences of a potential function at endpoints, Green's theorem relating it to a double integral, and Stokes' theorem relating it to a surface integral.

5. Line Integral Of
Vector Field

6. What is Vector?

7. Definition of vector:
A vector is an object that
has both a magnitude and a direction.
Graphically:

8. Suppose your teacher tells you "A bag of gold is
located outside the classroom. To find it, displace
yourself 20 meters." This statement may provide
yourself enough information to pique your interest;
yet, there is not enough information included in the statement
to find the bag of gold. The displacement required to find
the bag of gold has not been fully described. On the other
hand, suppose your teacher tells you "A bag of gold is
located outside the classroom. To find it, displace yourself
from the center of the classroom door 20 meters in a
direction 30 degrees to the west of north." This statement
now provides a complete description of the displacement
vector - it lists both magnitude (20 meters) and direction
(30 degrees to the west of north) relative to a reference or
starting position (the center of the classroom door).

9. What is line Integral?

10. Definition of line integral:
The integral,
taken along a line,
of any function
that has a Continuously
varying value along that line.
A common technique in physics is to integrate
a vector field along a curve, i.e. to determine
its line integral.

11. What is Vector
Field?

12. Definition of Vector Field:
A region of space under the
influence of some vector quantity,
such as magnetic field strength, in
which the quantity takes a unique
vector value at every point of the
region.
Example:
Magnetic field is also
called vector field.

14. Definition of line integral of Vector Field:

16. The line integral of a vector field
plays a crucial role in vector calculus. Out of
the four fundamental theorems of vector
calculus, three of them involve line integrals
of vector fields.
The Gradiant Theorem of line integral,
Green’s Theorem and Stokes' theorem
relate line integrals around closed
curves to double integrals or surface
integrals.

17. The gradient theorem for line integrals relates a line
integral to the values of a function at the “boundary” of
the curve, i.e., its endpoints. It says that
∫C∇f⋅ds=f(q)−f(p),
where p and q are the endpoints of C. In words, this
means the line integral of the gradient of some function is
just the difference of the function evaluated at the
endpoints of the curve. In particular, this means that the
integral of ∇f does not depend on the curve itself. The
vector field ∇f is conservative (also called path-
independent).

18. Often, we are not given the potential function, but just the
integral in terms of a vector field F: ∫CF⋅ds.
We can use the gradient theorem only when F is
conservative, in which case we can find a potential
function f so that ∇f=F. Then,
∫CF⋅ds=f(q)−f(p),
where p and q are the endpoints of C.
Even if you can't find f,but still know that F is
conservative, you could use the gradient theorem for line
integrals to change the line integral of F over C to the line
integral of F over any other curve with the same
endpoints.

19. Green's theorem relates a double integral over a region to a
line integral over the boundary of the region. If a curve C is the
boundary of some region D, i.e., C=∂D, then Green's theorem
says that
∫CF⋅ds=∬D(∂F2∂x−∂F1∂y)dA,
as long as F is continously differentiable everywhere inside D.
The integrand of the double integral can be thought of as the
“microscopic circulation” of F. Green's theorem then says that
the total “microscopic circulation” in D is equal to the
circulation ∫CF⋅ds around the boundary C=∂D. Thinking of
Green's theorem in terms of circulation will help prevent you
from erroneously attempting to use it when C is an open
curve.
In order for Green's theorem to work, the curve C has to be
oriented properly. Outer boundaries must be counterclockwise
and inner boundaries must be clockwise.

20. Stokes' theorem relates a line integral over a closed
curve to a surface integral. If a path C is the boundary of
some surface S, i.e., C=∂S, then Stokes' theorem says
that
∫CF⋅ds=∬ScurlF⋅dS.
The integrand of the surface integral can be thought of as
the “microscopic circulation” of F. Stokes' theorem then
says that the total “microscopic circulation” in S is equal to
the circulation ∫CF⋅ds around the boundary C=∂S. Thinking
of Stokes' theorem in terms of circulation will help prevent
you from erroneously attempting to use it when C is an
open curve.

21. In order for Stokes' theorem to work, the curve C has
to be a positively oriented boundary of the surface S.
To check for proper orientation, use the right hand
rule.
Since the line integral ∫CF⋅ds depends only on the
boundary of S (remember C=∂S), the surface
integral on the right hand side of Stokes' theorem
must also depend only on the boundary of S.
Therefore, Stokes' theorem says you can change the
surface to another surface S′, as long as ∂S′=∂S.
This works, of course, only when integrating the
vector field curlF over a surface; it won't work for any
arbitrary vector field.

25. ANY
QUESTIONS?