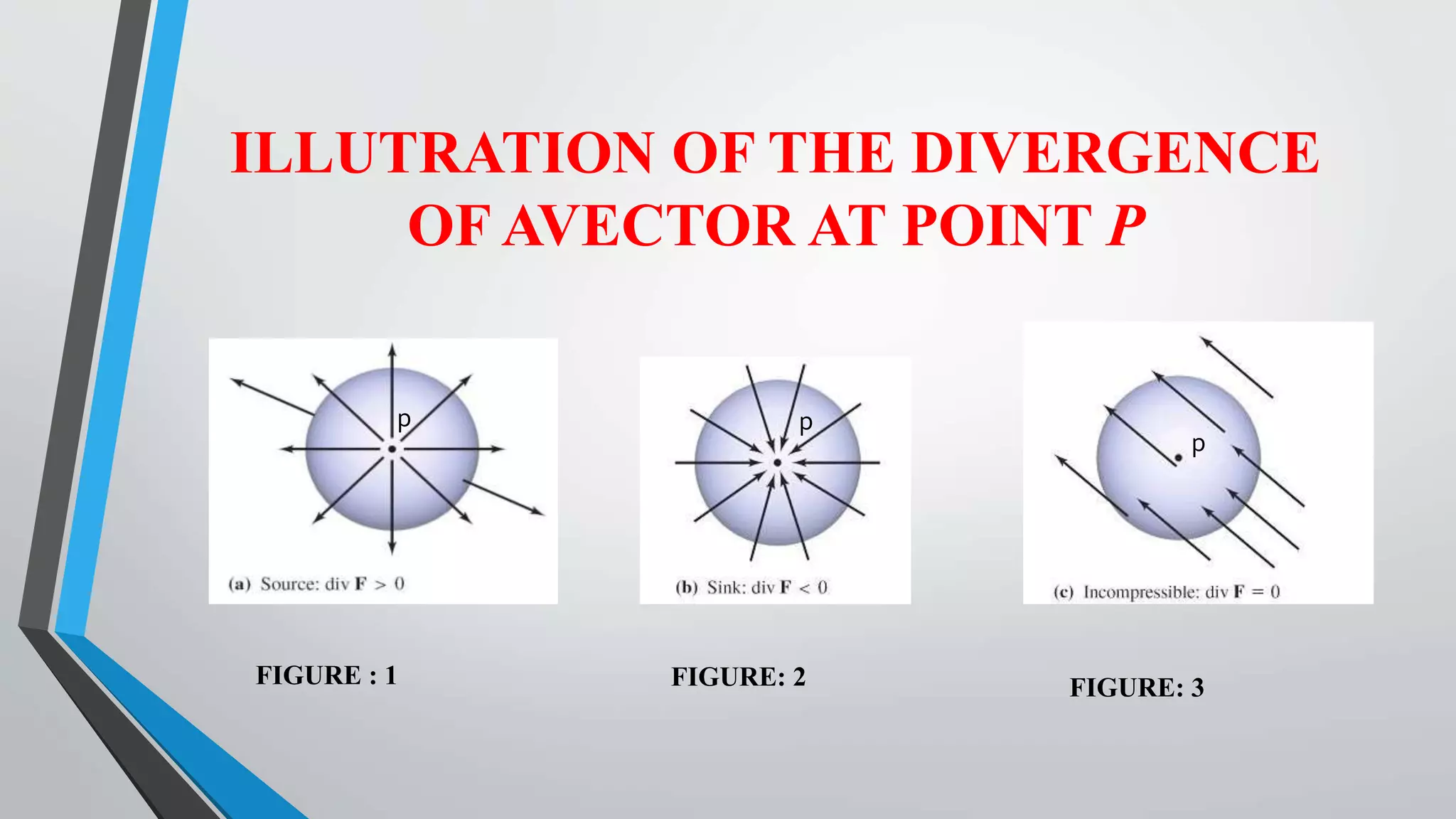
This document discusses the divergence of a vector field and the divergence theorem. It begins by defining the divergence of a vector field as a measure of how much that field diverges from a given point. It then illustrates the divergence of a vector field can be positive, negative, or zero at a point. The document expresses the divergence in Cartesian, cylindrical, and spherical coordinate systems. It proves the divergence theorem, which states that the outward flux of a vector field through a closed surface is equal to the volume integral of the divergence of the field over the enclosed volume. The document provides two examples applying the divergence theorem to calculate outward fluxes.

1. G.H.PATEL COLLEGE OF
ENGINNERING AND
TECHNOLOGY
NAME:
KOTHADIA YASH – 150110109019
LALKIYAABHISHEK -150110109020
VASOYA MAULIK - 150110109060

2. DIVERGENCE OF A VECTOR
AND DIVERGENCE
THEOREM

3. INTRODUCTION
• DEFINITION:-
The divergence theorem sates that the total outward flux of a
vector field A through the closed surface S is the same as the volume integral of
the divergence of A.
• It is denoted by divA.
• It is also know as gauss- ostrogradsky theorem.

4. ILLUTRATION OF THE DIVERGENCE
OF AVECTOR AT POINT P
FIGURE : 1 FIGURE: 2 FIGURE: 3
p p
p

5. • Where ∆v is the volume enclose bye the surface S in which P is located.
• Physically, we may regard the divergence of a vector field A at a given point
as measure of how much the field diverges from that point.
• Figure 1 show that the divergence of a vector field ay point P is positive
because the vector diverges at P.
• Figure 2 a vector field has negative divergence at P.
• Figure a vector field has zero divergence at P.
• The divergence of a vector field can be as simply the limit of the field’s
source strength per unit volume.

6. EXPRESS IN CRTESIAN COORDINATE
SYSTEM
FIGURE : 4

7. • We wish to evaluate the divergence of a vector field A at point P(𝒙 𝟎, 𝒚 𝟎, 𝒛 𝟎).
• We let the point be enclosed by a differential volume as in figure 4.
• The surface integral is obtain from
• 𝐴 ∙ 𝑑𝑆=( 𝑓𝑟𝑜𝑛𝑡
+ 𝑏𝑎𝑐𝑘
+ 𝑙𝑒𝑓𝑡
+ 𝑟𝑖𝑔ℎ𝑡
+ 𝑡𝑜𝑝
+ 𝑏𝑜𝑡𝑡𝑜𝑚
) A∙dS………..(1)
• A three-dimensional Taylor series expansion of Ax about P is
• A(x, y, z)=𝐴 𝑥(𝑥0, 𝑦0, 𝑧0)+(x-𝑥0)
𝜕𝐴 𝑥
𝜕𝑥
∣ 𝑝+(y-𝑦0)
𝜕𝐴 𝑦
𝜕𝑦
∣ 𝑝+(z-𝑧0)
𝜕𝐴 𝑧
𝜕𝑧
∣ 𝑝+higher term....(2)

8. • For the front side, x =𝑥0+dx/2 and dS = dy dz 𝑎 𝑥. Then,
• 𝑓𝑟𝑜𝑛𝑡
𝐴 ∙ 𝑑𝑆 = dy dz[𝐴 𝑥(𝑥0, 𝑦0, 𝑧0)+
𝑑𝑥
2
𝜕𝐴 𝑥
𝜕𝑥
∣ 𝑝]+higher-order term
• For the back side, x =𝑥0 −dx/2 and dS = dy dz (−𝑎 𝑥). Then,
• 𝑏𝑎𝑐𝑘
𝐴 ∙ 𝑑𝑆 = -dy dz[𝐴 𝑥(𝑥0, 𝑦0, 𝑧0)−
𝑑𝑥
2
𝜕𝐴 𝑥
𝜕𝑥
∣ 𝑝]+higher-order term
• Hence ,
• 𝑓𝑟𝑜𝑛𝑡
𝐴 ∙ 𝑑𝑆 + 𝑏𝑎𝑐𝑘
𝐴 ∙ 𝑑𝑆 = 𝑑𝑥 𝑑𝑦 𝑑𝑧
𝜕𝐴 𝑥
𝜕𝑥
∣ 𝑝+higher-order term…(3)
• By tacking similar step , we obtain
• 𝑙𝑒𝑓𝑡
𝐴 ∙ 𝑑𝑆 + 𝑟𝑖𝑔ℎ𝑡
𝐴 ∙ 𝑑𝑆 = 𝑑𝑥 𝑑𝑦 𝑑𝑧
𝜕𝐴 𝑦
𝜕𝑦
∣ 𝑝+higher-order term…..(4)

9. • and
• 𝑡𝑜𝑝
𝐴 ∙ 𝑑𝑆 + 𝑏𝑢𝑡𝑡𝑜𝑚
𝐴 ∙ 𝑑𝑆 = 𝑑𝑥 𝑑𝑦 𝑑𝑧
𝜕𝐴 𝑧
𝜕𝑧
∣ 𝑝+higher-order term….(5)
• Substituting eqs. 3, 4, 5 into eq. 1 and noting that ∆v=dx dy dz, we gate
• lim
∆v
⇾ 0
𝐴∙𝑑𝑆
∆v
= (
𝜕𝐴 𝑥
𝜕𝑥
+
𝜕𝐴 𝑦
𝜕𝑦
+
𝜕𝐴 𝑧
𝜕𝑧
) ∣ 𝑎𝑡 𝑝……(6)
• Because the higher order will vanish as ∆v ⇾ 𝟎. thus, the divergence of A at
point P(𝒙 𝟎, 𝒚 𝟎, 𝒛 𝟎) in Cartesian system is given by
• 𝛻∙A=
𝜕𝐴 𝑥
𝜕𝑥
+
𝜕𝐴 𝑦
𝜕𝑦
+
𝜕𝐴 𝑧
𝜕𝑧
……(7)

10. • similar the expressions for 𝜵∙A in other coordinate system can be obtained
directly or by transforming eq.7 into the appropriate system.
• In cylindrical coordinate, substituting
• 𝛻∙A=
1
𝜌
𝜕
𝜕𝜌
(𝜌𝐴 𝜌)+
1
𝜌
𝜕𝐴∅
𝜕𝜌
+
𝜕𝐴 𝑧
𝜕𝑧
…….(8)
• In spherical coordinate as
• 𝛻∙A=
1
𝑟2
𝜕
𝜕𝑟
(𝑟2 𝐴 𝑟)+
1
𝑟𝑠𝑖𝑛𝜭
𝜕
𝜕𝜭
(𝐴 𝜭sin𝜭)+
1
𝑟𝑠𝑖𝑛𝜭
𝜕𝐴∅
𝜕∅
…….(9)

11. FULX AND DIVERGENCE THEOREM
• The divergence theorem states that the outward flux of vector field A through
the closed surface s is the same as the volume integral of the divergence of A.
• This is called the divergence theorem, otherwise known as the Gauss-
Ostrogradsky theorem.
• To prove the divergence theorem , subdivide volume v into a large number of
small cell. If the kth cell has volume ∆𝒗 𝒌 and is bounded by surface 𝒔 𝒌.

12. • 𝐴 ∙ 𝑑𝑠 = 𝑘 𝑠 𝑓
𝐴 ∙ 𝑑𝑠 = 𝑘
𝑠 𝑘
𝐴∙𝑑𝑠
∆𝑣 𝑘
∆ 𝑣 𝑘………(10)
• Since the outward flux to one cell is inward to some neighboring cell, there is
cancellation on every interior surface , so the sum of the surface integral over
𝒔 𝒌
′
𝒔 is the same as the surface integral over the surface s. Taking the limit of
the right-hand side of above equation.
• 𝑠
𝐴 ∙ 𝑑𝑠 = 𝑣𝛻
𝛻 ∙ 𝐴 𝑑𝑣 … … … (11)
• Which is divergence theorem. The theory applied to any volume v
bounded by the closed surface S such as that shown in fig.5

13. Figure : 5
• It is provided that A and ∇∙A are continuous in the region.
• With little experience, it will soon become apparent that volume
integral are easier the evaluate than surface integral.
• For this region, to determine the flux of A through a closed surface
we simply find the right hand of eq.11 instead of the left hand side
of the equation.

14. EXAMPLES
EXAMPLE:1 Let Q be the region bounded by the sphere x2 + y2 + z2 = 4.
Find the outward flux of the vector field
F(x, y, z) = 2x3i + 2y3j + 2z3k
through the sphere.
Solution:
By the Divergence Theorem, you have

16. EXAMPLE:2 Let Q be the solid region bounded by the coordinate planes and
the plane 2x + 2y + z = 6, and let F = xi + y2j + zk.
Find
where S is the surface of Q.
Solution:
From Figure 15.56,
you can see that Q is bounded
by four subsurface. FIGURE:6

17. So, you would need four surface integrals to evaluate
However, by the Divergence Theorem, you need only one triple integral.
Because
you have