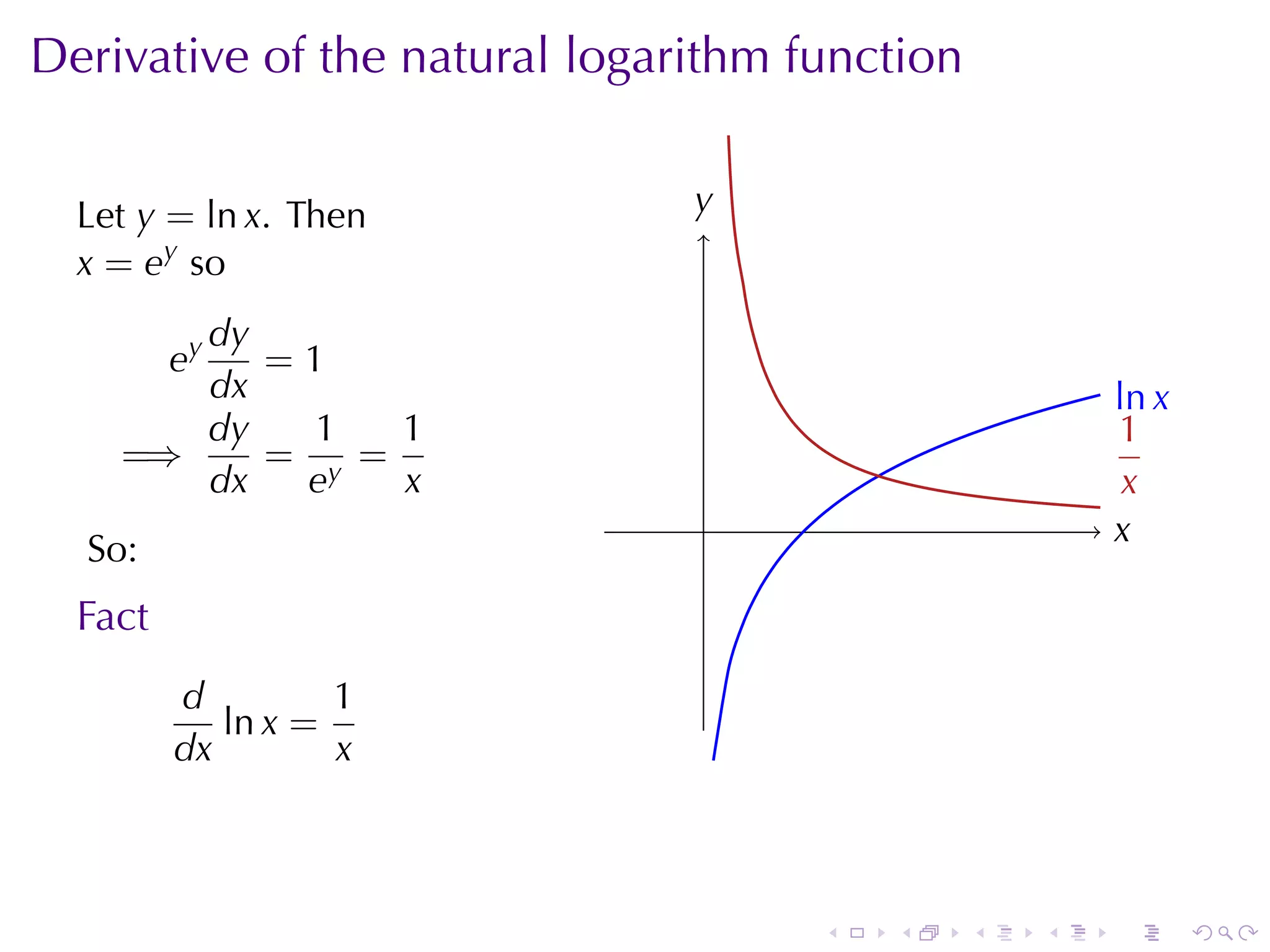
The document discusses the derivatives of exponential and logarithmic functions, outlining key concepts such as the derivative of the natural exponential function, the natural logarithm, and various rules for differentiating exponential and logarithmic expressions. It emphasizes that the derivative of an exponential function is proportional to the function itself and provides examples for finding specific derivatives. Additionally, the document covers techniques like logarithmic differentiation and the power rule for irrational powers.

1. Section 3.3
Derivatives of Exponential and
Logarithmic Functions
V63.0121.027, Calculus I
October 22, 2009
.
.
Image credit: heipei
. . . . . .

2. Outline
Derivative of the natural exponential function
Exponential Growth
Derivative of the natural logarithm function
Derivatives of other exponentials and logarithms
Other exponentials
Other logarithms
Logarithmic Differentiation
The power rule for irrational powers
. . . . . .

3. Derivatives of Exponential Functions
Fact
If f(x) = ax , then f′ (x) = f′ (0)ax .
. . . . . .

4. Derivatives of Exponential Functions
Fact
If f(x) = ax , then f′ (x) = f′ (0)ax .
Proof.
Follow your nose:
f(x + h) − f(x) a x+ h − a x
f′ (x) = lim = lim
h→0 h h→0 h
a x a h − ax a h−1
= lim = ax · lim = ax · f′ (0).
h→0 h h→0 h
. . . . . .

5. Derivatives of Exponential Functions
Fact
If f(x) = ax , then f′ (x) = f′ (0)ax .
Proof.
Follow your nose:
f(x + h) − f(x) a x+ h − a x
f′ (x) = lim = lim
h→0 h h→0 h
a x a h − ax a h−1
= lim = ax · lim = ax · f′ (0).
h→0 h h→0 h
To reiterate: the derivative of an exponential function is a
constant times that function. Much different from polynomials!
. . . . . .

6. The funny limit in the case of e
Remember the definition of e:
( )
1 n
e = lim 1 + = lim (1 + h)1/h
n→∞ n h→0
Question
eh − 1
What is lim ?
h→0 h
. . . . . .

7. The funny limit in the case of e
Remember the definition of e:
( )
1 n
e = lim 1 + = lim (1 + h)1/h
n→∞ n h→0
Question
eh − 1
What is lim ?
h→0 h
Answer
If h is small enough, e ≈ (1 + h)1/h . So
[ ]h
eh − 1 (1 + h)1/h − 1 (1 + h) − 1 h
≈ = = =1
h h h h
. . . . . .

8. The funny limit in the case of e
Remember the definition of e:
( )
1 n
e = lim 1 + = lim (1 + h)1/h
n→∞ n h→0
Question
eh − 1
What is lim ?
h→0 h
Answer
If h is small enough, e ≈ (1 + h)1/h . So
[ ]h
eh − 1 (1 + h)1/h − 1 (1 + h) − 1 h
≈ = = =1
h h h h
eh − 1
So in the limit we get equality: lim =1
h→0 h
. . . . . .

9. Derivative of the natural exponential function
From
( )
d x ah − 1 eh − 1
a = lim ax and lim =1
dx h→0 h h→0 h
we get:
Theorem
d x
e = ex
dx
. . . . . .

10. Exponential Growth
Commonly misused term to say something grows
exponentially
It means the rate of change (derivative) is proportional to the
current value
Examples: Natural population growth, compounded interest,
social networks
. . . . . .

11. Examples
Examples
Find these derivatives:
e3x
2
ex
x 2 ex
. . . . . .

12. Examples
Examples
Find these derivatives:
e3x
2
ex
x 2 ex
Solution
d 3x
e = 3e3x
dx
. . . . . .

13. Examples
Examples
Find these derivatives:
e3x
2
ex
x 2 ex
Solution
d 3x
e = 3e3x
dx
d x2 2 d 2
e = ex (x2 ) = 2xex
dx dx
. . . . . .

14. Examples
Examples
Find these derivatives:
e3x
2
ex
x 2 ex
Solution
d 3x
e = 3e3x
dx
d x2 2 d 2
e = ex (x2 ) = 2xex
dx dx
d 2 x
x e = 2xex + x2 ex
dx
. . . . . .

15. Outline
Derivative of the natural exponential function
Exponential Growth
Derivative of the natural logarithm function
Derivatives of other exponentials and logarithms
Other exponentials
Other logarithms
Logarithmic Differentiation
The power rule for irrational powers
. . . . . .

16. Derivative of the natural logarithm function
Let y = ln x. Then
x = ey so
. . . . . .

17. Derivative of the natural logarithm function
Let y = ln x. Then
x = ey so
dy
ey =1
dx
. . . . . .

18. Derivative of the natural logarithm function
Let y = ln x. Then
x = ey so
dy
ey =1
dx
dy 1 1
=⇒ = y =
dx e x
. . . . . .

19. Derivative of the natural logarithm function
Let y = ln x. Then
x = ey so
dy
ey
=1
dx
dy 1 1
=⇒ = y =
dx e x
So:
Fact
d 1
ln x =
dx x
. . . . . .

20. Derivative of the natural logarithm function
Let y = ln x. Then y
.
x = ey so
dy
ey
=1
dx .n x
l
dy 1 1
=⇒ = y =
dx e x
. x
.
So:
Fact
d 1
ln x =
dx x
. . . . . .

21. Derivative of the natural logarithm function
Let y = ln x. Then y
.
x = ey so
dy
ey
=1
dx .n x
l
dy 1 1 1
=⇒ = y = .
dx e x x
. x
.
So:
Fact
d 1
ln x =
dx x
. . . . . .

22. The Tower of Powers
y y′
The derivative of a
x3 3x2 power function is a
power function of one
x2 2x1
lower power
x1 1x0
x0 0
? ?
x−1 −1x−2
x−2 −2x−3
. . . . . .

23. The Tower of Powers
y y′
The derivative of a
x3 3x2 power function is a
power function of one
x2 2x1
lower power
x1 1x0 Each power function is
x 0
0 the derivative of another
power function, except
? x −1 x−1
x−1 −1x−2
x−2 −2x−3
. . . . . .

24. The Tower of Powers
y y′
The derivative of a
x3 3x2 power function is a
power function of one
x2 2x1
lower power
x1 1x0 Each power function is
x 0
0 the derivative of another
power function, except
ln x x −1 x−1
x−1 −1x−2 ln x fills in this gap
precisely.
x−2 −2x−3
. . . . . .

25. Outline
Derivative of the natural exponential function
Exponential Growth
Derivative of the natural logarithm function
Derivatives of other exponentials and logarithms
Other exponentials
Other logarithms
Logarithmic Differentiation
The power rule for irrational powers
. . . . . .

26. Other logarithms
Example
d x
Use implicit differentiation to find a.
dx
. . . . . .

27. Other logarithms
Example
d x
Use implicit differentiation to find a.
dx
Solution
Let y = ax , so
ln y = ln ax = x ln a
. . . . . .

28. Other logarithms
Example
d x
Use implicit differentiation to find a.
dx
Solution
Let y = ax , so
ln y = ln ax = x ln a
Differentiate implicitly:
1 dy dy
= ln a =⇒ = (ln a)y = (ln a)ax
y dx dx
. . . . . .

29. Other logarithms
Example
d x
Use implicit differentiation to find a.
dx
Solution
Let y = ax , so
ln y = ln ax = x ln a
Differentiate implicitly:
1 dy dy
= ln a =⇒ = (ln a)y = (ln a)ax
y dx dx
Before we showed y′ = y′ (0)y, so now we know that
2h − 1 3h − 1
ln 2 = lim ≈ 0.693 ln 3 = lim ≈ 1.10
h→0 h h→0 h
. . . . . .

30. Other logarithms
Example
d
Find loga x.
dx
. . . . . .

31. Other logarithms
Example
d
Find loga x.
dx
Solution
Let y = loga x, so ay = x.
. . . . . .

32. Other logarithms
Example
d
Find loga x.
dx
Solution
Let y = loga x, so ay = x. Now differentiate implicitly:
dy dy 1 1
(ln a)ay = 1 =⇒ = y =
dx dx a ln a x ln a
. . . . . .

33. Other logarithms
Example
d
Find loga x.
dx
Solution
Let y = loga x, so ay = x. Now differentiate implicitly:
dy dy 1 1
(ln a)ay = 1 =⇒ = y =
dx dx a ln a x ln a
Another way to see this is to take the natural logarithm:
ln x
ay = x =⇒ y ln a = ln x =⇒ y =
ln a
dy 1 1
So = .
dx ln a x
. . . . . .

34. More examples
Example
d
Find log2 (x2 + 1)
dx
. . . . . .

35. More examples
Example
d
Find log2 (x2 + 1)
dx
Answer
dy 1 1 2x
= 2+1
(2x) =
dx ln 2 x (ln 2)(x2 + 1)
. . . . . .

36. Outline
Derivative of the natural exponential function
Exponential Growth
Derivative of the natural logarithm function
Derivatives of other exponentials and logarithms
Other exponentials
Other logarithms
Logarithmic Differentiation
The power rule for irrational powers
. . . . . .

37. A nasty derivative
Example √
(x2 + 1) x + 3
Let y = . Find y′ .
x−1
. . . . . .

38. A nasty derivative
Example √
(x2 + 1) x + 3
Let y = . Find y′ .
x−1
Solution
We use the quotient rule, and the product rule in the numerator:
[ √ ] √
′ (x − 1) 2x x + 3 + (x2 + 1) 1 (x + 3)−1/2 − (x2 + 1) x + 3(1)
2
y =
(x − 1)2
√ √
2x x + 3 (x2 + 1) (x 2 + 1 ) x + 3
= + √ −
(x − 1 ) 2 x + 3(x − 1) (x − 1)2
. . . . . .

39. Another way
√
(x 2 + 1 ) x + 3
y=
x−1
1
ln y = ln(x2 + 1) + ln(x + 3) − ln(x − 1)
2
1 dy 2x 1 1
= 2 + −
y dx x + 1 2(x + 3) x − 1
So
( )
dy 2x 1 1
= + − y
dx x2 + 1 2(x + 3) x − 1
( ) √
2x 1 1 (x2 + 1) x + 3
= + −
x2 + 1 2(x + 3) x − 1 x−1
. . . . . .

40. Compare and contrast
Using the product, quotient, and power rules:
√ √
′ 2x x + 3 (x2 + 1) (x2 + 1) x + 3
y = + √ −
(x − 1) 2 x + 3(x − 1) (x − 1)2
Using logarithmic differentiation:
( ) √
′ 2x 1 1 (x2 + 1) x + 3
y = + −
x2 + 1 2(x + 3) x − 1 x−1
. . . . . .

41. Compare and contrast
Using the product, quotient, and power rules:
√ √
′ 2x x + 3 (x2 + 1) (x2 + 1) x + 3
y = + √ −
(x − 1) 2 x + 3(x − 1) (x − 1)2
Using logarithmic differentiation:
( ) √
′ 2x 1 1 (x2 + 1) x + 3
y = + −
x2 + 1 2(x + 3) x − 1 x−1
Are these the same?
. . . . . .

42. Compare and contrast
Using the product, quotient, and power rules:
√ √
′ 2x x + 3 (x2 + 1) (x2 + 1) x + 3
y = + √ −
(x − 1) 2 x + 3(x − 1) (x − 1)2
Using logarithmic differentiation:
( ) √
′ 2x 1 1 (x2 + 1) x + 3
y = + −
x2 + 1 2(x + 3) x − 1 x−1
Are these the same?
Which do you like better?
. . . . . .

43. Compare and contrast
Using the product, quotient, and power rules:
√ √
′ 2x x + 3 (x2 + 1) (x2 + 1) x + 3
y = + √ −
(x − 1) 2 x + 3(x − 1) (x − 1)2
Using logarithmic differentiation:
( ) √
′ 2x 1 1 (x2 + 1) x + 3
y = + −
x2 + 1 2(x + 3) x − 1 x−1
Are these the same?
Which do you like better?
What kinds of expressions are well-suited for logarithmic
differentiation?
. . . . . .

44. Derivatives of powers
Let y = xx . Which of these is true?
(A) Since y is a power function, y′ = x · xx−1 = xx .
(B) Since y is an exponential function, y′ = (ln x) · xx
(C) Neither
. . . . . .

45. Derivatives of powers
Let y = xx . Which of these is true?
(A) Since y is a power function, y′ = x · xx−1 = xx .
(B) Since y is an exponential function, y′ = (ln x) · xx
(C) Neither
. . . . . .

46. It’s neither! Or both?
If y = xx , then
ln y = x ln x
1 dy 1
= x · + ln x = 1 + ln x
y dx x
dy
= xx + (ln x)xx
dx
Each of these terms is one of the wrong answers!
. . . . . .

47. Derivative of arbitrary powers
Fact (The power rule)
Let y = xr . Then y′ = rxr−1 .
. . . . . .

48. Derivative of arbitrary powers
Fact (The power rule)
Let y = xr . Then y′ = rxr−1 .
Proof.
y = xr =⇒ ln y = r ln x
Now differentiate:
1 dy r
=
y dx x
dy y
=⇒ = r = rxr−1
dx x
. . . . . .