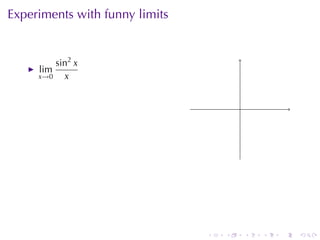
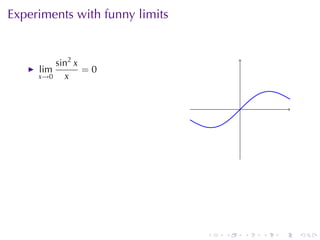
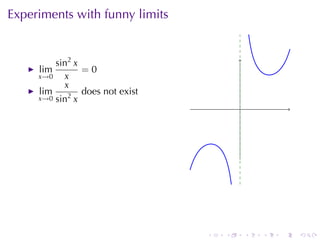
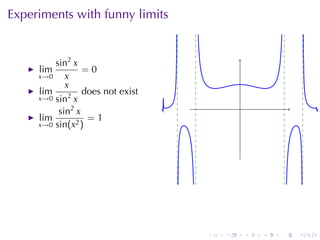
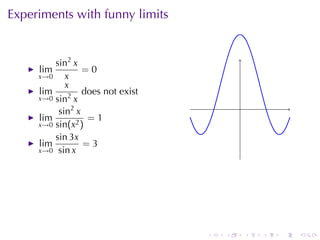
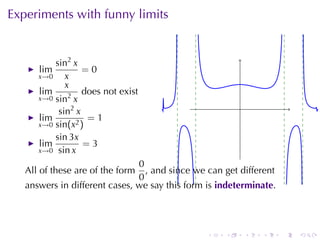
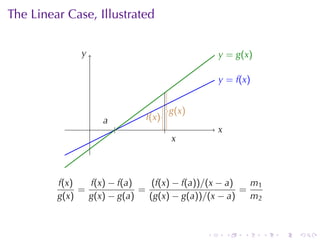
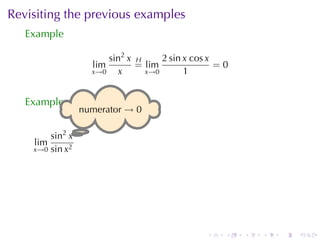
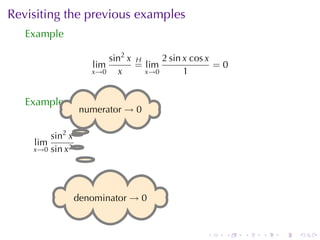
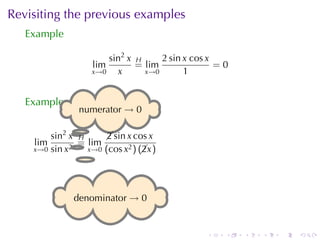
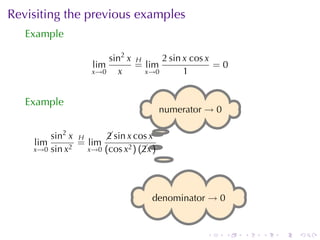
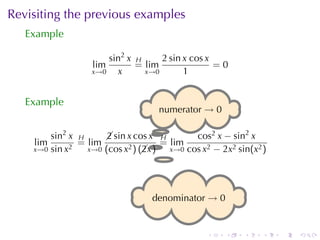
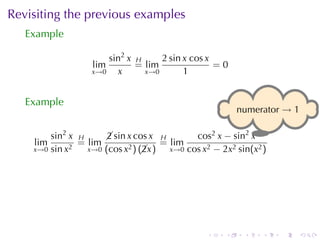
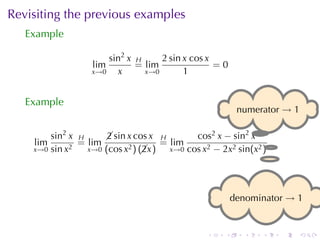
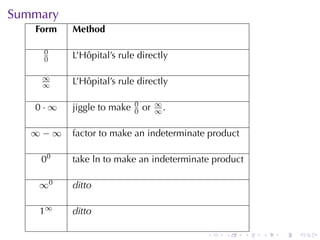
The document discusses indeterminate forms and L'Hôpital's rule in calculus, detailing how to handle limits when both the numerator and denominator approach zero or infinity. It explains the conditions under which L'Hôpital's rule applies and provides examples to illustrate how to evaluate limits using differentiation. The document emphasizes the importance of understanding limit laws and offers insights into the behavior of various functions near specific points.

1. Section 3.7
Indeterminate Forms and L’Hôpital’s
Rule
V63.0121.027, Calculus I
November 3, 2009
Announcements
Quiz next week in section
. . . . . .

2. Experiments with funny limits
sin2 x
lim
x→0 x
.
. . . . . .

3. Experiments with funny limits
sin2 x
lim =0
x→0 x
.
. . . . . .

4. Experiments with funny limits
sin2 x
lim =0
x→0 x
x
lim
x→0 sin2 x
.
. . . . . .

5. Experiments with funny limits
sin2 x
lim =0
x→0 x
x
lim does not exist
x→0 sin2 x
.
. . . . . .

6. Experiments with funny limits
sin2 x
lim =0
x→0 x
x
lim does not exist
x→0 sin2 x
sin2 x .
lim
x→0 sin(x2 )
. . . . . .

7. Experiments with funny limits
sin2 x
lim =0
x→0 x
x
lim does not exist
x→0 sin2 x
sin2 x .
lim =1
x→0 sin(x2 )
. . . . . .

8. Experiments with funny limits
sin2 x
lim =0
x→0 x
x
lim does not exist
x→0 sin2 x
sin2 x .
lim =1
x→0 sin(x2 )
sin 3x
lim
x→0 sin x
. . . . . .

9. Experiments with funny limits
sin2 x
lim =0
x→0 x
x
lim does not exist
x→0 sin2 x
sin2 x .
lim =1
x→0 sin(x2 )
sin 3x
lim =3
x→0 sin x
. . . . . .

10. Experiments with funny limits
sin2 x
lim =0
x→0 x
x
lim does not exist
x→0 sin2 x
sin2 x .
lim =1
x→0 sin(x2 )
sin 3x
lim =3
x→0 sin x
0
All of these are of the form , and since we can get different
0
answers in different cases, we say this form is indeterminate.
. . . . . .

11. Outline
Indeterminate Forms
L’Hôpital’s Rule
Relative Rates of Growth
Other Indeterminate Limits
Indeterminate Products
Indeterminate Differences
Indeterminate Powers
Summary
. . . . . .

12. Recall
Recall the limit laws from Chapter 2.
Limit of a sum is the sum of the limits
. . . . . .

13. Recall
Recall the limit laws from Chapter 2.
Limit of a sum is the sum of the limits
Limit of a difference is the difference of the limits
. . . . . .

14. Recall
Recall the limit laws from Chapter 2.
Limit of a sum is the sum of the limits
Limit of a difference is the difference of the limits
Limit of a product is the product of the limits
. . . . . .

15. Recall
Recall the limit laws from Chapter 2.
Limit of a sum is the sum of the limits
Limit of a difference is the difference of the limits
Limit of a product is the product of the limits
Limit of a quotient is the quotient of the limits ... whoops!
This is true as long as you don’t try to divide by zero.
. . . . . .

16. We know dividing by zero is bad.
Most of the time, if an expression’s numerator approaches a
finite number and denominator approaches zero, the
quotient approaches some kind of infinity. For example:
1 cos x
lim = +∞ lim = −∞
x→0+ x x→0− x3
. . . . . .

17. We know dividing by zero is bad.
Most of the time, if an expression’s numerator approaches a
finite number and denominator approaches zero, the
quotient approaches some kind of infinity. For example:
1 cos x
lim = +∞ lim = −∞
x→0+ x x→0− x3
An exception would be something like
1
lim = lim x csc x.
x→∞ 1 sin x x→∞
x
which doesn’t exist.
. . . . . .

18. We know dividing by zero is bad.
Most of the time, if an expression’s numerator approaches a
finite number and denominator approaches zero, the
quotient approaches some kind of infinity. For example:
1 cos x
lim = +∞ lim = −∞
x→0+ x x→0− x3
An exception would be something like
1
lim = lim x csc x.
x→∞ 1 sin x x→∞
x
which doesn’t exist.
Even less predictable: numerator and denominator both go
to zero.
. . . . . .

19. Language Note
It depends on what the meaning of the word “is” is
Be careful with the
language here. We are
not saying that the limit
0
in each case “is” , and
0
therefore nonexistent
because this expression
is undefined.
The limit is of the form
0
, which means we
0
cannot evaluate it with
our limit laws.
. . . . . .

20. Indeterminate forms are like Tug Of War
Which side wins depends on which side is stronger.
. . . . . .

21. Outline
Indeterminate Forms
L’Hôpital’s Rule
Relative Rates of Growth
Other Indeterminate Limits
Indeterminate Products
Indeterminate Differences
Indeterminate Powers
Summary
. . . . . .

22. The Linear Case
Question
If f and g are lines and f(a) = g(a) = 0, what is
f(x)
lim ?
x→a g(x)
. . . . . .

23. The Linear Case
Question
If f and g are lines and f(a) = g(a) = 0, what is
f(x)
lim ?
x→a g(x)
Solution
The functions f and g can be written in the form
f(x) = m1 (x − a)
g(x) = m2 (x − a)
So
f (x ) m1
=
g (x ) m2
. . . . . .

24. The Linear Case, Illustrated
y
. y
. = g(x)
y
. = f(x)
g
. (x)
a
. f
.(x)
. . . x
.
x
.
f(x) f(x) − f(a) (f(x) − f(a))/(x − a) m1
= = =
g(x) g(x) − g(a) (g(x) − g(a))/(x − a) m2
. . . . . .

25. What then?
But what if the functions aren’t linear?
. . . . . .

26. What then?
But what if the functions aren’t linear?
Can we approximate a function near a point with a linear
function?
. . . . . .

27. What then?
But what if the functions aren’t linear?
Can we approximate a function near a point with a linear
function?
What would be the slope of that linear function?
. . . . . .

28. What then?
But what if the functions aren’t linear?
Can we approximate a function near a point with a linear
function?
What would be the slope of that linear function? The
derivative!
. . . . . .

29. Theorem (L’Hopital’s Rule)
Suppose f and g are differentiable functions and g′ (x) ̸= 0 near a
(except possibly at a). Suppose that
lim f(x) = 0 and lim g(x) = 0
x→a x→a
or
lim f(x) = ±∞ and lim g(x) = ±∞
x→a x→a
Then
f(x) f′ (x)
lim = lim ′ ,
x→a g(x) x→a g (x)
if the limit on the right-hand side is finite, ∞, or −∞.
. . . . . .

30. Meet the Mathematician: L’Hôpital
wanted to be a military
man, but poor eyesight
forced him into math
did some math on his
own (solved the
“brachistocrone
problem”)
paid a stipend to Johann
Bernoulli, who proved
this theorem and named
it after him! Guillaume François Antoine,
Marquis de L’Hôpital
(1661–1704)
. . . . . .

31. Revisiting the previous examples
Example
sin2 x
lim
x→0 x
. . . . . .

32. Revisiting the previous examples
Example
sin2 x H 2 sin x cos x
lim = lim
x→0 x x→0 1
. . . . . .

33. Revisiting the previous examples
Example . in x → 0
s
sin2 x H 2 sin x.cos x
lim = lim
x→0 x x→0 1
. . . . . .

34. Revisiting the previous examples
Example . in x → 0
s
sin2 x H 2 sin x.cos x
lim = lim =0
x→0 x x→0 1
. . . . . .

35. Revisiting the previous examples
Example . in x → 0
s
sin2 x H 2 sin x.cos x
lim = lim =0
x→0 x x→0 1
Example
sin2 x
lim
x→0 sin x2
. . . . . .

36. Revisiting the previous examples
Example
sin2 x H 2 sin x cos x
lim = lim =0
x→0 x x→0 1
Example
. umerator → 0
n
sin2 x.
lim
x→0 sin x2
. . . . . .

37. Revisiting the previous examples
Example
sin2 x H 2 sin x cos x
lim = lim =0
x→0 x x→0 1
Example
. umerator → 0
n
sin2 x.
lim .
x→0 sin x2
. enominator → 0
d
. . . . . .

38. Revisiting the previous examples
Example
sin2 x H 2 sin x cos x
lim = lim =0
x→0 x x→0 1
Example
. umerator → 0
n
sin2 x. H sin x cos x
2
lim 2.
= lim
x→0 sin x x→0 (cos x2 ) (x )
2
. enominator → 0
d
. . . . . .

39. Revisiting the previous examples
Example
sin2 x H 2 sin x cos x
lim = lim =0
x→0 x x→0 1
Example
. umerator → 0
n
sin2 x H .
sin x cos x
2
lim = lim
x→0 sin x2 x→0 (cos x2 ) (x )
2
. . . . . .

40. Revisiting the previous examples
Example
sin2 x H 2 sin x cos x
lim = lim =0
x→0 x x→0 1
Example
. umerator → 0
n
sin2 x H .
sin x cos x
2
lim = lim .)
x→0 sin x2 x→0 (cos x2 ) (x
2
. enominator → 0
d
. . . . . .

41. Revisiting the previous examples
Example
sin2 x H 2 sin x cos x
lim = lim =0
x→0 x x→0 1
Example
. umerator → 0
n
sin2 x H . cos2 x − sin2 x
sin x cos x H
2
lim = lim lim
.) = x→0 cos x2 − 2x2 sin(x2 )
x→0 sin x2 x→0 (cos x2 ) (x
2
. enominator → 0
d
. . . . . .

42. Revisiting the previous examples
Example
sin2 x H 2 sin x cos x
lim = lim =0
x→0 x x→0 1
Example
. umerator → 1
n
sin2 x H sin x cos x H
2 cos2 x − sin2 x.
lim = lim = lim
x→0 sin x2 x→0 (cos x2 ) (x )
2 x→0 cos x2 − 2x2 sin(x2 )
. . . . . .

43. Revisiting the previous examples
Example
sin2 x H 2 sin x cos x
lim = lim =0
x→0 x x→0 1
Example
. umerator → 1
n
sin2 x H sin x cos x H
2 cos2 x − sin2 x.
lim = lim = lim .
x→0 sin x2 x→0 (cos x2 ) (x )
2 x→0 cos x2 − 2x2 sin(x2 )
. enominator → 1
d
. . . . . .

44. Revisiting the previous examples
Example
sin2 x H 2 sin x cos x
lim = lim =0
x→0 x x→0 1
Example
sin2 x H sin x cos x H
2 cos2 x − sin2 x
lim = lim = lim =1
x→0 sin x2 x→0 (cos x2 ) (x )
2 x→0 cos x2 − 2x2 sin(x2 )
. . . . . .

45. Revisiting the previous examples
Example
sin2 x H 2 sin x cos x
lim = lim =0
x→0 x x→0 1
Example
sin2 x H sin x cos x H
2 cos2 x − sin2 x
lim = lim = lim =1
x→0 sin x2 x→0 (cos x2 ) (x )
2 x→0 cos x2 − 2x2 sin(x2 )
Example
sin 3x H 3 cos 3x
lim = lim = 3.
x→0 sin x x→0 cos x
. . . . . .

46. Example
Find
x
lim
x→0 cos x
. . . . . .

47. Beware of Red Herrings
Example
Find
x
lim
x→0 cos x
Solution
The limit of the denominator is 1, not 0, so L’Hôpital’s rule does
not apply. The limit is 0.
. . . . . .

48. Outline
Indeterminate Forms
L’Hôpital’s Rule
Relative Rates of Growth
Other Indeterminate Limits
Indeterminate Products
Indeterminate Differences
Indeterminate Powers
Summary
. . . . . .

49. Theorem
Let r be any positive number. Then
ex
lim = ∞.
x→∞ xr
. . . . . .

50. Theorem
Let r be any positive number. Then
ex
lim = ∞.
x→∞ xr
Proof.
If r is a positive integer, then apply L’Hôpital’s rule r times to the
fraction. You get
ex H H ex
lim = . . . = lim = ∞.
x→∞ xr x→∞ r!
For example, if r = 3, three invocations of L’Hôpital’s Rule give us
ex H ex H ex H ex
lim = lim = lim = lim =∞
x→∞ x3 x→∞ 3 · x2 x→∞ 3 · 2x x→∞ 3 · 2 · 1
. . . . . .

51. If r is not an integer, let m be the smallest integer greater than r.
Then if x 1, xr xm , so
ex ex
m.
xr x
The right-hand side tends to ∞ by the previous step.
. . . . . .

52. If r is not an integer, let m be the smallest integer greater than r.
Then if x 1, xr xm , so
ex ex
m.
xr x
The right-hand side tends to ∞ by the previous step. For
example, if r = 1/2, r 1 so for x 1
ex ex
x1/2 x
which gets arbitrarily large.
. . . . . .

53. Theorem
Let r be any positive number. Then
ln x
lim = 0.
x→∞ xr
. . . . . .

54. Theorem
Let r be any positive number. Then
ln x
lim = 0.
x→∞ xr
Proof.
One application of L’Hôpital’s Rule here suffices:
ln x H 1 /x 1
lim = lim r−1 = lim r = 0.
x→∞ xr x→∞ rx x→∞ rx
. . . . . .

55. Outline
Indeterminate Forms
L’Hôpital’s Rule
Relative Rates of Growth
Other Indeterminate Limits
Indeterminate Products
Indeterminate Differences
Indeterminate Powers
Summary
. . . . . .

56. Indeterminate products
Example
Find √
lim x ln x
x→0+
This limit is of the form 0 · (−∞).
. . . . . .

57. Indeterminate products
Example
Find √
lim x ln x
x→0+
This limit is of the form 0 · (−∞).
Solution
Jury-rig the expression to make an indeterminate quotient. Then
apply L’Hôpital’s Rule:
√
lim x ln x
x→0+
. . . . . .

58. Indeterminate products
Example
Find √
lim x ln x
x→0+
This limit is of the form 0 · (−∞).
Solution
Jury-rig the expression to make an indeterminate quotient. Then
apply L’Hôpital’s Rule:
√ ln x
lim x ln x = lim
x→0+ x→0+ 1/√x
. . . . . .

59. Indeterminate products
Example
Find √
lim x ln x
x→0+
This limit is of the form 0 · (−∞).
Solution
Jury-rig the expression to make an indeterminate quotient. Then
apply L’Hôpital’s Rule:
√ ln x H x−1
lim x ln x = lim √ = lim 1
x→0+ x→0+ 1/ x x→0+ − 2 x−3/2
. . . . . .

60. Indeterminate products
Example
Find √
lim x ln x
x→0+
This limit is of the form 0 · (−∞).
Solution
Jury-rig the expression to make an indeterminate quotient. Then
apply L’Hôpital’s Rule:
√ ln x H x−1
lim x ln x = lim √ = lim 1
x→0+ x→0+ 1/ x x→0+ − 2 x−3/2
√
= lim −2 x
x→0+
. . . . . .

61. Indeterminate products
Example
Find √
lim x ln x
x→0+
This limit is of the form 0 · (−∞).
Solution
Jury-rig the expression to make an indeterminate quotient. Then
apply L’Hôpital’s Rule:
√ ln x H x−1
lim x ln x = lim √ = lim 1
x→0+ x→0+ 1/ x x→0+ − 2 x−3/2
√
= lim −2 x = 0
x→0+
. . . . . .

62. Indeterminate differences
Example
( )
1
lim − cot 2x
x→0+ x
This limit is of the form ∞ − ∞.
. . . . . .

63. Indeterminate differences
Example
( )
1
lim − cot 2x
x→0+ x
This limit is of the form ∞ − ∞.
Solution
Again, rig it to make an indeterminate quotient.
sin(2x) − x cos(2x)
lim
x→0+ x sin(2x)
. . . . . .

64. Indeterminate differences
Example
( )
1
lim − cot 2x
x→0+ x
This limit is of the form ∞ − ∞.
Solution
Again, rig it to make an indeterminate quotient.
sin(2x) − x cos(2x) H cos(2x) + 2x sin(2x)
lim = lim+
x→0+ x sin(2x) x→0 2x cos(2x) + sin(2x)
. . . . . .

65. Indeterminate differences
Example
( )
1
lim − cot 2x
x→0+ x
This limit is of the form ∞ − ∞.
Solution
Again, rig it to make an indeterminate quotient.
sin(2x) − x cos(2x) H cos(2x) + 2x sin(2x)
lim = lim+
x→0+ x sin(2x) x→0 2x cos(2x) + sin(2x)
=∞
. . . . . .

66. Indeterminate differences
Example
( )
1
lim − cot 2x
x→0+ x
This limit is of the form ∞ − ∞.
Solution
Again, rig it to make an indeterminate quotient.
sin(2x) − x cos(2x) H cos(2x) + 2x sin(2x)
lim = lim+
x→0+ x sin(2x) x→0 2x cos(2x) + sin(2x)
=∞
The limit is +∞ becuase the numerator tends to 1 while the
denominator tends to zero but remains positive.
. . . . . .

67. Checking your work
.
tan 2x
lim = 1, so for small x,
x→0 2x
1
tan 2x ≈ 2x. So cot 2x ≈ and
. 2x
1 1 1 1
− cot 2x ≈ − = →∞
x x 2x 2x
as x → 0+ .
. . . . . .

68. Indeterminate powers
Example
Find lim (1 − 2x)1/x
x→0+
. . . . . .

69. Indeterminate powers
Example
Find lim (1 − 2x)1/x
x→0+
Take the logarithm:
( ) ( )
1/x ln(1 − 2x)
ln lim (1 − 2x) = lim+ ln (1 − 2x)1/x = lim+
x→0 + x→0 x→0 x
. . . . . .

70. Indeterminate powers
Example
Find lim (1 − 2x)1/x
x→0+
Take the logarithm:
( ) ( )
1/x ln(1 − 2x)
ln lim (1 − 2x) = lim+ ln (1 − 2x)1/x = lim+
x→0 + x→0 x→0 x
0
This limit is of the form , so we can use L’Hôpital:
0
−2
ln(1 − 2x) H 1−2x
lim = lim+ = −2
x→0+ x x→0 1
. . . . . .

71. Indeterminate powers
Example
Find lim (1 − 2x)1/x
x→0+
Take the logarithm:
( ) ( )
1/x ln(1 − 2x)
ln lim (1 − 2x) = lim+ ln (1 − 2x)1/x = lim+
x→0 + x→0 x→0 x
0
This limit is of the form , so we can use L’Hôpital:
0
−2
ln(1 − 2x) H 1−2x
lim = lim+ = −2
x→0+ x x→0 1
This is not the answer, it’s the log of the answer! So the answer
we want is e−2 .
. . . . . .

72. Example
lim (3x)4x
x→0
. . . . . .

73. Example
lim (3x)4x
x→0
Solution
ln lim (3x)4x = lim ln(3x)4x = lim 4x ln(3x)
x→0+ x→0+ x→0+
ln(3x) H 3/3x
= lim+ = lim+
x→0 1/4x x→0 −1/4x2
= lim (−4x) = 0
x→0+
So the answer is e0 = 1.
. . . . . .

74. Outline
Indeterminate Forms
L’Hôpital’s Rule
Relative Rates of Growth
Other Indeterminate Limits
Indeterminate Products
Indeterminate Differences
Indeterminate Powers
Summary
. . . . . .

75. Summary
Form Method
0
0 L’Hôpital’s rule directly
∞
∞ L’Hôpital’s rule directly
0 ∞
0·∞ jiggle to make 0 or ∞.
∞−∞ factor to make an indeterminate product
00 take ln to make an indeterminate product
∞0 ditto
1∞ ditto
. . . . . .

76. Final thoughts
L’Hôpital’s Rule only works on indeterminate quotients
Luckily, most indeterminate limits can be transformed into
indeterminate quotients
L’Hôpital’s Rule gives wrong answers for non-indeterminate
limits!
. . . . . .