This document is the outline for a calculus class. It discusses the final exam date and review sessions, and outlines the topics of substitution for indefinite integrals and substitution for definite integrals. It provides an example of using substitution to find the integral of the square root of x^2 + 1 by letting u = x^2 + 1, and expresses this using both standard notation and Leibniz notation. It states the theorem of substitution rule.

1. Section 5.5
Integration by Substitution
V63.0121.027, Calculus I
December 10, 2009
Announcements
Final Exam: Friday 12/18, 2:00-3:50pm, Tisch UC50
Practice finals on the website. Solutions Friday
. . . . . .

2. Schedule for next week
Tuesday, 8:00am: Review session for all students with 8:00
recitations (Tuesday or Thursday) in CIWW 109
Tuesday, 9:30am: Review session for all students with 9:30
recitations (Tuesday or Thursday) in CIWW 109
Office Hours continue
Tuesday, class: review, evaluations, movie!
Friday, 2:00pm: final in Tisch UC50
. . . . . .

3. Resurrection Policy
If your final score beats your midterm score, we will add 10% to
its weight, and subtract 10% from the midterm weight.
.
.
Image credit: Scott Beale / Laughing Squid
. . . . . .

4. Outline
Last Time: The Fundamental Theorem(s) of Calculus
Substitution for Indefinite Integrals
Theory
Examples
Substitution for Definite Integrals
Theory
Examples
. . . . . .

5. Differentiation and Integration as reverse processes
Theorem (The Fundamental Theorem of Calculus)
1. Let f be continuous on [a, b]. Then
∫ x
d
f(t) dt = f(x)
dx a
2. Let f be continuous on [a, b] and f = F′ for some other
function F. Then
∫ b
f(x) dx = F(b) − F(a).
a
. . . . . .

6. Techniques of antidifferentiation?
So far we know only a few rules for antidifferentiation. Some are
general, like
∫ ∫ ∫
[f(x) + g(x)] dx = f(x) dx + g(x) dx
. . . . . .

7. Techniques of antidifferentiation?
So far we know only a few rules for antidifferentiation. Some are
general, like
∫ ∫ ∫
[f(x) + g(x)] dx = f(x) dx + g(x) dx
Some are pretty particular, like
∫
1
√ dx = arcsec x + C.
x x2 − 1
. . . . . .

8. Techniques of antidifferentiation?
So far we know only a few rules for antidifferentiation. Some are
general, like
∫ ∫ ∫
[f(x) + g(x)] dx = f(x) dx + g(x) dx
Some are pretty particular, like
∫
1
√ dx = arcsec x + C.
x x2 − 1
What are we supposed to do with that?
. . . . . .

9. So far we don’t have any way to find
∫
2x
√ dx
x2 + 1
or ∫
tan x dx.
. . . . . .

10. So far we don’t have any way to find
∫
2x
√ dx
x2 + 1
or ∫
tan x dx.
Luckily, we can be smart and use the “anti” version of one of the
most important rules of differentiation: the chain rule.
. . . . . .

11. Outline
Last Time: The Fundamental Theorem(s) of Calculus
Substitution for Indefinite Integrals
Theory
Examples
Substitution for Definite Integrals
Theory
Examples
. . . . . .

12. Substitution for Indefinite Integrals
Example
Find ∫
x
√ dx.
x 2+1
. . . . . .

13. Substitution for Indefinite Integrals
Example
Find ∫
x
√ dx.
x 2+1
Solution
Stare at this long enough and you notice the the integrand is the
√
derivative of the expression 1 + x2 .
. . . . . .

14. Say what?
Solution (More slowly, now)
Let g(x) = x2 + 1.
. . . . . .

15. Say what?
Solution (More slowly, now)
Let g(x) = x2 + 1. Then g′ (x) = 2x and so
d√ 1 x
g(x) = √ g′ (x) = √
dx 2 g(x) x2 + 1
. . . . . .

16. Say what?
Solution (More slowly, now)
Let g(x) = x2 + 1. Then g′ (x) = 2x and so
d√ 1 x
g(x) = √ g′ (x) = √
dx 2 g(x) x2 + 1
Thus
∫ ∫ ( )
x d√
√ dx = g(x) dx
x2 + 1 dx
√ √
= g(x) + C = 1 + x2 + C.
. . . . . .

17. Leibnizian notation FTW
Solution (Same technique, new notation)
Let u = x2 + 1.
. . . . . .

18. Leibnizian notation FTW
Solution (Same technique, new notation)
√ √
Let u = x2 + 1. Then du = 2x dx and 1 + x2 = u.
. . . . . .

19. Leibnizian notation FTW
Solution (Same technique, new notation)
√ √
Let u = x2 + 1. Then du = 2x dx and 1 + x2 = u. So the
integrand becomes completely transformed into
∫ ∫ 1 ∫
√
x dx 2 du
√
1
√ du
= =
x2 + 1 u 2 u
. . . . . .

20. Leibnizian notation FTW
Solution (Same technique, new notation)
√ √
Let u = x2 + 1. Then du = 2x dx and 1 + x2 = u. So the
integrand becomes completely transformed into
∫ ∫ 1 ∫
√
x dx 2 du
√
1
√ du
= =
x2 + 1 ∫ u 2 u
1 −1/2
= 2u du
. . . . . .

21. Leibnizian notation FTW
Solution (Same technique, new notation)
√ √
Let u = x2 + 1. Then du = 2x dx and 1 + x2 = u. So the
integrand becomes completely transformed into
∫ ∫ 1 ∫
√
x dx 2 du
√
1
√ du
= =
x2 + 1 ∫ u 2 u
1 −1/2
= 2u du
√ √
= u+C= 1 + x2 + C.
. . . . . .

22. Useful but unsavory variation
Solution (Same technique, new notation, more idiot-proof)
√ √
Let u = x2 + 1. Then du = 2x dx and 1 + x2 = u. “Solve for
dx:”
du
dx =
2x
So the integrand becomes completely transformed into
∫ ∫ ∫
x x du 1
√ dx = √ · = √ du
x2 + 1 u 2x 2 u
∫
1 −1/2
= 2u du
√ √
= u + C = 1 + x2 + C .
Mathematicians have serious issues with mixing the x and u like
this. However, I can’t deny that it works.
. . . . . .

23. Theorem of the Day
Theorem (The Substitution Rule)
If u = g(x) is a differentiable function whose range is an interval I
and f is continuous on I, then
∫ ∫
f(g(x))g′ (x) dx = f(u) du
That is, if F is an antiderivative for f, then
∫
f(g(x))g′ (x) dx = F(g(x))
In Leibniz notation:
∫ ∫
du
f(u) dx = f(u) du
dx
. . . . . .

24. A polynomial example
Example ∫
Use the substitution u = x2 + 3 to find (x2 + 3)3 4x dx.
. . . . . .

25. A polynomial example
Example ∫
Use the substitution u = x2 + 3 to find (x2 + 3)3 4x dx.
Solution
If u = x2 + 3, then du = 2x dx, and 4x dx = 2 du. So
∫ ∫ ∫
(x + 3) 4x dx = u 2du = 2 u3 du
2 3 3
1 4 1 2
= u = (x + 3)4
2 2
. . . . . .

26. A polynomial example, by brute force
Compare this to multiplying it out:
∫ ∫
2 3
( 6 )
(x + 3) 4x dx = x + 9x4 + 27x2 + 27 4x dx
∫
( 7 )
= 4x + 36x5 + 108x3 + 108x dx
1 8
= x + 6x6 + 27x4 + 54x2
2
. . . . . .

27. A polynomial example, by brute force
Compare this to multiplying it out:
∫ ∫
2 3
( 6 )
(x + 3) 4x dx = x + 9x4 + 27x2 + 27 4x dx
∫
( 7 )
= 4x + 36x5 + 108x3 + 108x dx
1 8
= x + 6x6 + 27x4 + 54x2
2
Which would you rather do?
. . . . . .

28. A polynomial example, by brute force
Compare this to multiplying it out:
∫ ∫
2 3
( 6 )
(x + 3) 4x dx = x + 9x4 + 27x2 + 27 4x dx
∫
( 7 )
= 4x + 36x5 + 108x3 + 108x dx
1 8
= x + 6x6 + 27x4 + 54x2
2
Which would you rather do?
It’s a wash for low powers
But for higher powers, it’s much easier to do substitution.
. . . . . .

29. Compare
We have the substitution method, which, when multiplied out,
gives
∫
1
(x2 + 3)3 4x dx = (x2 + 3)4
2
1( 8 )
= x + 12x6 + 54x4 + 108x2 + 81
2
1 81
= x8 + 6x6 + 27x4 + 54x2 +
2 2
and the brute force method
∫
1
(x2 + 3)3 4x dx = x8 + 6x6 + 27x4 + 54x2
2
Is this a problem?
. . . . . .

30. Compare
We have the substitution method, which, when multiplied out,
gives
∫
1
(x2 + 3)3 4x dx = (x2 + 3)4 + C
2
1( 8 )
= x + 12x6 + 54x4 + 108x2 + 81 + C
2
1 81
= x8 + 6x6 + 27x4 + 54x2 + +C
2 2
and the brute force method
∫
1
(x2 + 3)3 4x dx = x8 + 6x6 + 27x4 + 54x2 + C
2
Is this a problem? No, that’s what +C means!
. . . . . .

31. A slick example
Example
∫
Find tan x dx.
. . . . . .

32. A slick example
Example
∫
sin x
Find tan x dx. (Hint: tan x = )
cos x
. . . . . .

33. A slick example
Example
∫
sin x
Find tan x dx. (Hint: tan x = )
cos x
Solution
Let u = cos x. Then du = − sin x dx.
. . . . . .

34. A slick example
Example
∫
sin x
Find tan x dx. (Hint: tan x = )
cos x
Solution
Let u = cos x. Then du = − sin x dx. So
∫ ∫ ∫
sin x 1
tan x dx = dx = − du
cos x u
. . . . . .

35. A slick example
Example
∫
sin x
Find tan x dx. (Hint: tan x = )
cos x
Solution
Let u = cos x. Then du = − sin x dx. So
∫ ∫ ∫
sin x 1
tan x dx = dx = − du
cos x u
= − ln |u| + C
. . . . . .

36. A slick example
Example
∫
sin x
Find tan x dx. (Hint: tan x = )
cos x
Solution
Let u = cos x. Then du = − sin x dx. So
∫ ∫ ∫
sin x 1
tan x dx = dx = − du
cos x u
= − ln |u| + C
= − ln | cos x| + C = ln | sec x| + C
. . . . . .

37. Can you do it another way?
Example
∫
sin x
Find tan x dx. (Hint: tan x = )
cos x
. . . . . .

38. Can you do it another way?
Example
∫
sin x
Find tan x dx. (Hint: tan x = )
cos x
Solution
du
Let u = sin x. Then du = cos x dx and so dx = .
cos x
. . . . . .

39. Can you do it another way?
Example
∫
sin x
Find tan x dx. (Hint: tan x = )
cos x
Solution
du
Let u = sin x. Then du = cos x dx and so dx = .
cos x
∫ ∫ ∫
sin x u du
tan x dx = dx =
cos x cos x cos x
∫ ∫ ∫
u du u du u du
= = 2
=
cos2 x 1 − sin x 1 − u2
At this point, although it’s possible to proceed, we should
probably back up and see if the other way works quicker (it
does).
. . . . . .

40. For those who really must know all
Solution (Continued, with algebra help)
∫ ∫ ∫ ( )
u du 1 1 1
tan x dx = = − du
1 − u2 2 1−u 1+u
1 1
= − ln |1 − u| − ln |1 + u| + C
2 2
1 1
= ln √ + C = ln √ +C
(1 − u)(1 + u) 1 − u2
1
= ln + C = ln |sec x| + C
|cos x|
. . . . . .

41. Outline
Last Time: The Fundamental Theorem(s) of Calculus
Substitution for Indefinite Integrals
Theory
Examples
Substitution for Definite Integrals
Theory
Examples
. . . . . .

42. Theorem (The Substitution Rule for Definite Integrals)
If g′ is continuous and f is continuous on the range of u = g(x),
then ∫ ∫
b g(b)
f(g(x))g′ (x) dx = f(u) du.
a g (a )
. . . . . .

43. Theorem (The Substitution Rule for Definite Integrals)
If g′ is continuous and f is continuous on the range of u = g(x),
then ∫ ∫
b g(b)
f(g(x))g′ (x) dx = f(u) du.
a g (a )
Why the change in the limits?
The integral on the left happens in “x-land”
The integral on the right happens in “u-land”, so the limits
need to be u-values
To get from x to u, apply g
. . . . . .

44. Example ∫
π
Compute cos2 x sin x dx.
0
. . . . . .

45. Example ∫
π
Compute cos2 x sin x dx.
0
Solution (Slow Way) ∫
First compute the indefinite integral cos2 x sin x dx and then
evaluate.
. . . . . .

46. Example ∫
π
Compute cos2 x sin x dx.
0
Solution (Slow Way) ∫
First compute the indefinite integral cos2 x sin x dx and then
evaluate. Let u = cos x. Then du = − sin x dx and
∫ ∫
cos x sin x dx = − u2 du
2
= − 1 u3 + C = − 1 cos3 x + C.
3 3
Therefore
∫ π
1 π
1( ) 2
cos2 x sin x dx = − cos3 x =− (−1)3 − 13 = .
0 3 0 3 3
. . . . . .

47. Solution (Fast Way)
Do both the substitution and the evaluation at the same time.
. . . . . .

48. Solution (Fast Way)
Do both the substitution and the evaluation at the same time. Let
u = cos x. Then du = − sin x dx, u(0) = 1 and u(π) = −1.
. . . . . .

49. Solution (Fast Way)
Do both the substitution and the evaluation at the same time. Let
u = cos x. Then du = − sin x dx, u(0) = 1 and u(π) = −1. So
∫ π ∫ −1
cos2 x sin x dx = −u2 du
0 1
∫ 1
= u2 du
−1
1
1 1( ) 2
= u3 = 1 − (−1) =
3 −1 3 3
. . . . . .

50. Solution (Fast Way)
Do both the substitution and the evaluation at the same time. Let
u = cos x. Then du = − sin x dx, u(0) = 1 and u(π) = −1. So
∫ π ∫ −1
cos2 x sin x dx = −u2 du
0 1
∫ 1
= u2 du
−1
1
1 1( ) 2
= u3 = 1 − (−1) =
3 −1 3 3
The advantage to the “fast way” is that you completely
transform the integral into something simpler and don’t have
to go back to the original x variable.
But the slow way is just as reliable.
. . . . . .

51. An exponential example
Example√
∫ ln 8 √
Find √ e2x e2x + 1 dx
ln 3
. . . . . .

52. An exponential example
Example√
∫ ln 8 √
Find √ e2x e2x + 1 dx
ln 3
Solution
Let u = e2x , so du = 2e2x dx. We have
∫ √ ∫
ln 8 √ 1 8√
√ e2x e2x + 1 dx = u + 1 du
ln 3 2 3
. . . . . .

53. An exponential example
Example√
∫ ln 8 √
Find √ e2x e2x + 1 dx
ln 3
Solution
Let u = e2x , so du = 2e2x dx. We have
∫ √ ∫
ln 8 √ 1 8√
√ e2x e2x + 1 dx = u + 1 du
ln 3 2 3
Now let y = u + 1, dy = du. So
∫ 8√ ∫ 9 ∫ 9
1 1 √ 1
u + 1 du = y dy = y1/2 dy
2 3 2 4 2 4
9
1 2 1 19
= · y3/2 = (27 − 8) =
2 3 4 3 3
. . . . . .

54. About those limits
√ √ 2
e2(ln 3)
= eln 3
= eln 3 = 3
. . . . . .

55. About those fractional powers
93/2 = (91/2 )3 = 33 = 27
43/2 = (41/2 )3 = 23 = 8
. . . . . .

56. Another way to skin that cat
Example√
∫ ln 8 √
Find √ e2x e2x + 1 dx
ln 3
Solution
Let u = e2x + 1
. . . . . .

57. Another way to skin that cat
Example√
∫ ln 8 √
Find √ e2x e2x + 1 dx
ln 3
Solution
Let u = e2x + 1, so that du = 2e2x dx.
. . . . . .

58. Another way to skin that cat
Example√
∫ ln 8 √
Find √ e2x e2x + 1 dx
ln 3
Solution
Let u = e2x + 1, so that du = 2e2x dx. Then
∫ √ ∫
ln 8 √ 1 9√
2x
√ e e2x + 1 dx = u du
ln 3 2 4
. . . . . .

59. Another way to skin that cat
Example√
∫ ln 8 √
Find √ e2x e2x + 1 dx
ln 3
Solution
Let u = e2x + 1, so that du = 2e2x dx. Then
∫ √ ∫
ln 8 √ 1 9√
2x
√ e e2x + 1 dx = u du
ln 3 2 4
9
1 3/2
= u
3 4
. . . . . .

60. Another way to skin that cat
Example√
∫ ln 8 √
Find √ e2x e2x + 1 dx
ln 3
Solution
Let u = e2x + 1, so that du = 2e2x dx. Then
∫ √ ∫
ln 8 √ 1 9√
2x
√ e e2x + 1 dx = u du
ln 3 2 4
1 3/2 9
= u
3 4
1 19
= (27 − 8) =
3 3
. . . . . .

61. A third skinned cat
Example√
∫ ln 8 √
Find √ e2x e2x + 1 dx
ln 3
Solution
√
Let u = e2x + 1, so that
u2 = e2x + 1
. . . . . .

62. A third skinned cat
Example√
∫ ln 8 √
Find √ e2x e2x + 1 dx
ln 3
Solution
√
Let u = e2x + 1, so that
u2 = e2x + 1 =⇒ 2u du = 2e2x dx
. . . . . .

63. A third skinned cat
Example√
∫ ln 8 √
Find √ e2x e2x + 1 dx
ln 3
Solution
√
Let u = e2x + 1, so that
u2 = e2x + 1 =⇒ 2u du = 2e2x dx
Thus ∫ √ ∫
ln 8 3 3
1 3 19
√ = u · u du = u =
ln 3 2 3 2 3
. . . . . .

64. Example
Find ∫ ( ) ( )
3π/2
5 θ 2 θ
cot sec dθ.
π 6 6
. . . . . .

65. Example
Find ∫ ( ) ( )
3π/2
5 θ 2 θ
cot sec dθ.
π 6 6
Before we dive in, think about:
What “easy” substitutions might help?
Which of the trig functions suggests a substitution?
. . . . . .

66. Solution
θ 1
Let φ = . Then dφ = dθ.
6 6
∫ 3π/2 ( ) ( ) ∫ π/4
5 θ 2 θ
cot sec dθ = 6 cot5 φ sec2 φ dφ
π 6 6 π/6
∫ π/4
sec2 φ dφ
=6
π/6 tan5 φ
. . . . . .

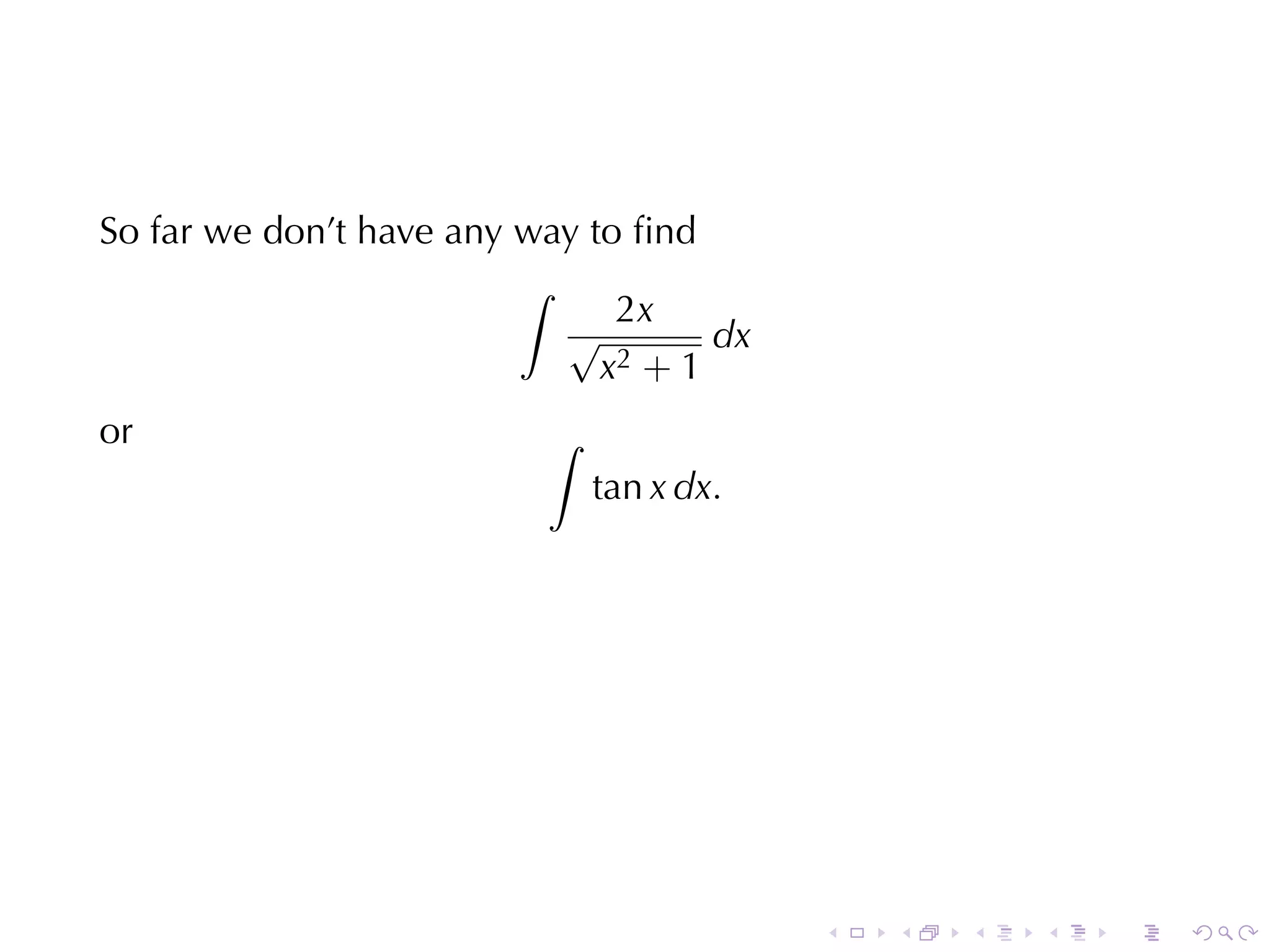
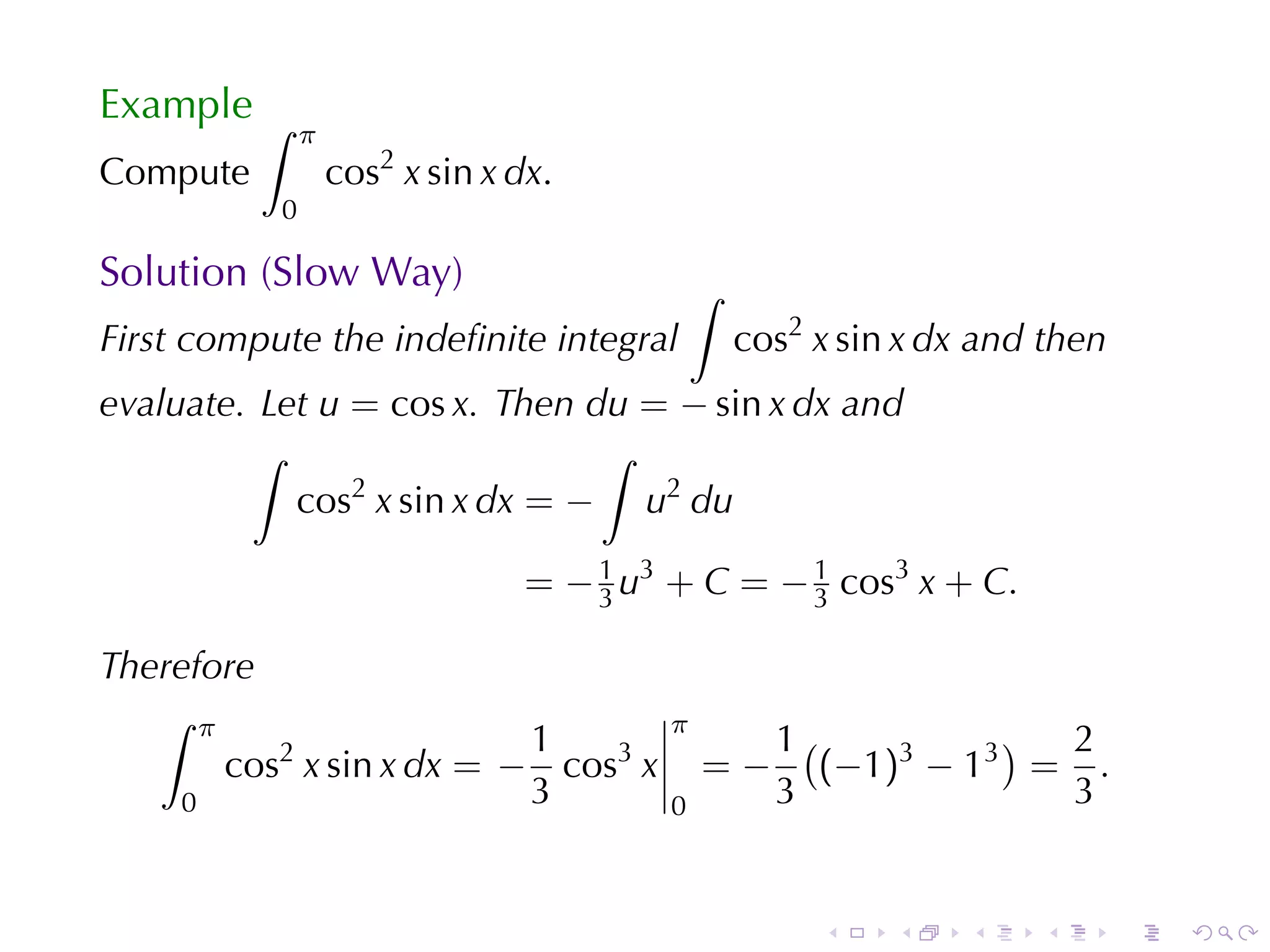
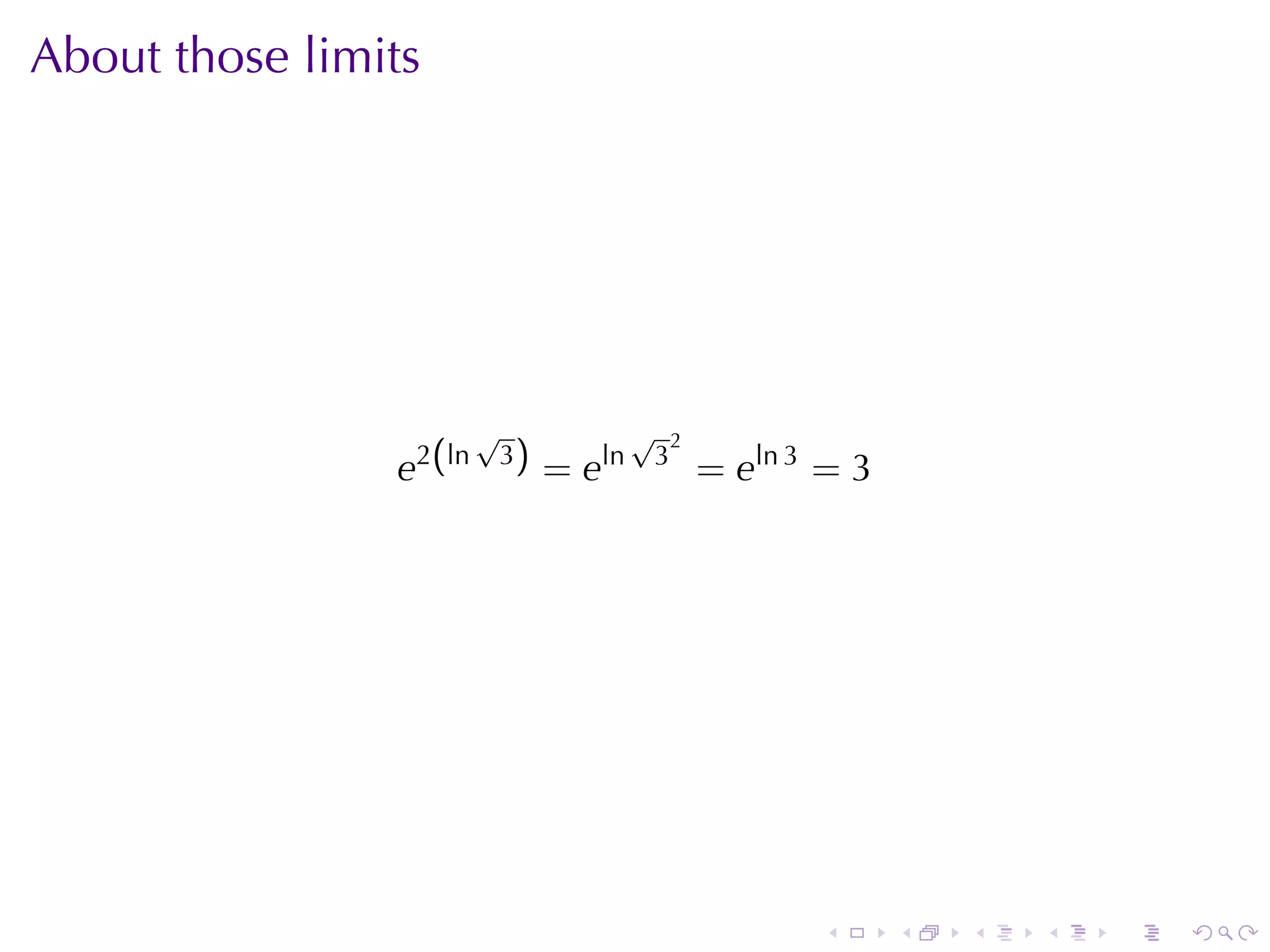
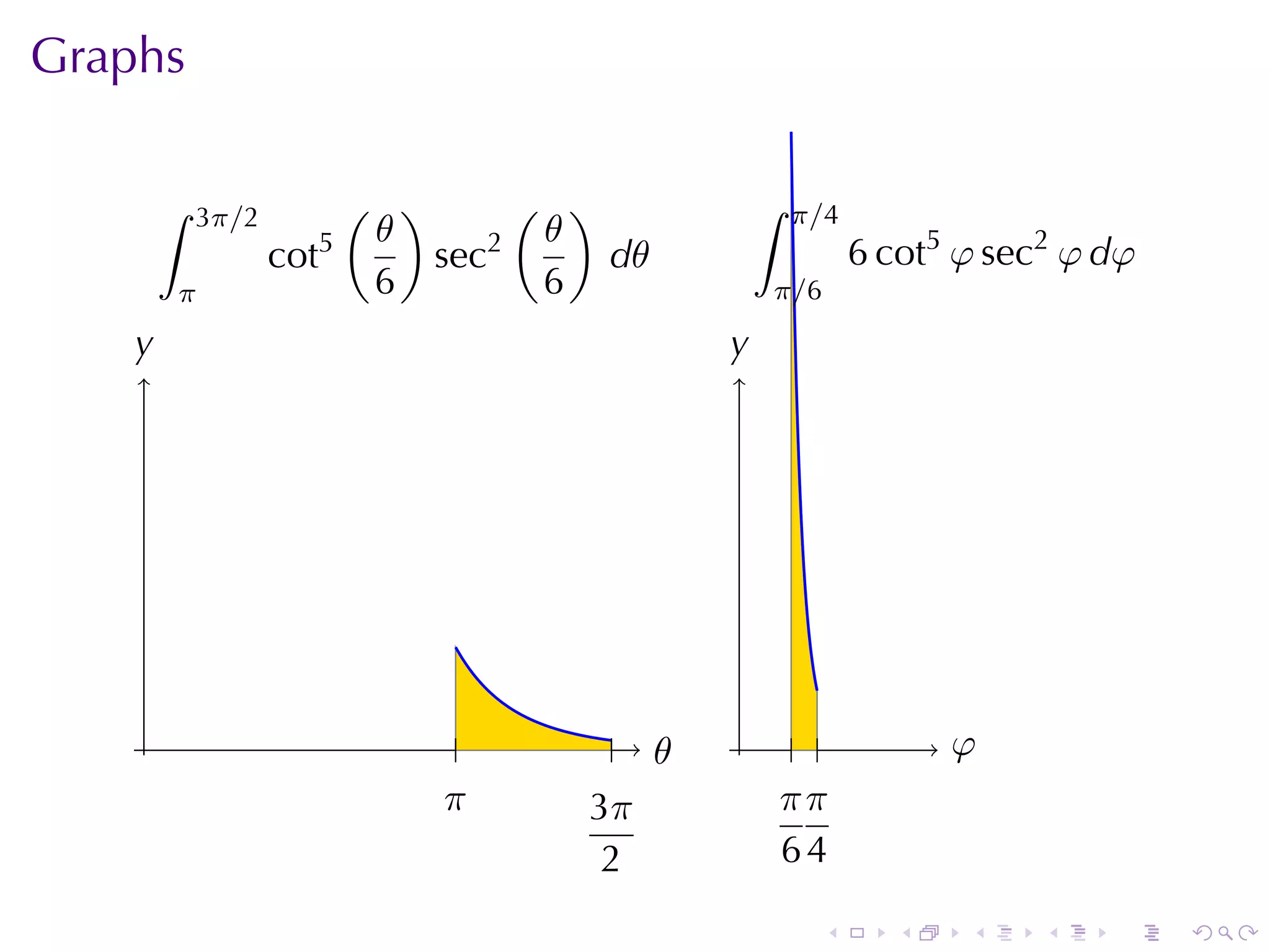
67. Solution
θ 1
Let φ = . Then dφ = dθ.
6 6
∫ 3π/2 ( ) ( ) ∫ π/4
5 θ 2 θ
cot sec dθ = 6 cot5 φ sec2 φ dφ
π 6 6 π/6
∫ π/4
sec2 φ dφ
=6
π/6 tan5 φ
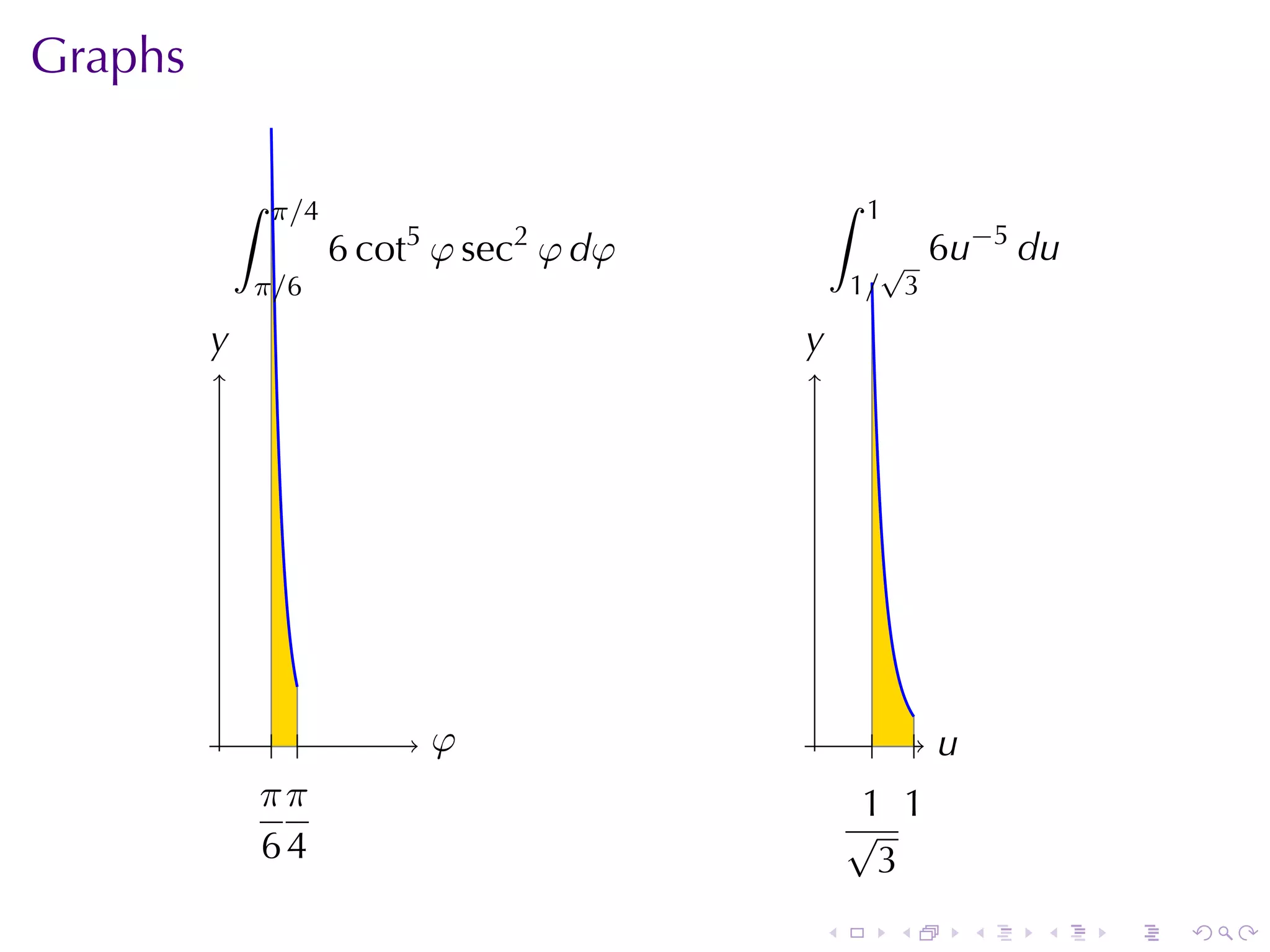
Now let u = tan φ. So du = sec2 φ dφ, and
∫ π/4 ∫ 1
sec2 φ dφ −5
6 =6 √ u du
π/6 tan5 φ 1/ 3
( ) 1
1 3
=6 − u−4 √
= [9 − 1] = 12.
4 1/ 3 2
. . . . . .

68. The limits explained
√
π sin π/4 2 /2
tan = =√ =1
4 cos π/4 2 /2
π sin π/6 1/2 1
tan = =√ =√
6 cos π/6 3 /2 3
. . . . . .

69. The limits explained
√
π sin π/4 2 /2
tan = =√ =1
4 cos π/4 2 /2
π sin π/6 1/2 1
tan = =√ =√
6 cos π/6 3 /2 3
( ) 1 √
1 −4 3 [ −4 ]1 √ 3 [ −4 ]1/ 3
6 − u √
= −u 1 / 3 = u 1
4 1/ 3 2 2
3 [ −1/2 −4 ]
= (3 ) − (1−1/2 )−4
2
3 3
= [32 − 12 ] = (9 − 1) = 12
2 2
. . . . . .

70. Graphs
∫ 3π/2 ( ) ( ) ∫ π/4
θ 2 θ
. 5
cot sec dθ . 6 cot5 φ sec2 φ dφ
π 6 6 π/6
y
. y
.
. . . .
θ . . .
φ
.
π 3π ππ
. . .
2 64
. . . . . .

71. Graphs
∫ π/4 ∫ 1
. 5 2
6 cot φ sec φ dφ . √ 6u−5 du
π/6 1/ 3
y
. y
.
. . . .
φ . ..
u
ππ 1 .1
. . .√
64 3
. . . . . .

72. Final Thoughts
Antidifferentiation is a “nonlinear” problem that needs
practice, intuition, and perserverance
Worksheet in recitation (also to be posted)
The whole antidifferentiation story is in Chapter 6
. . . . . .