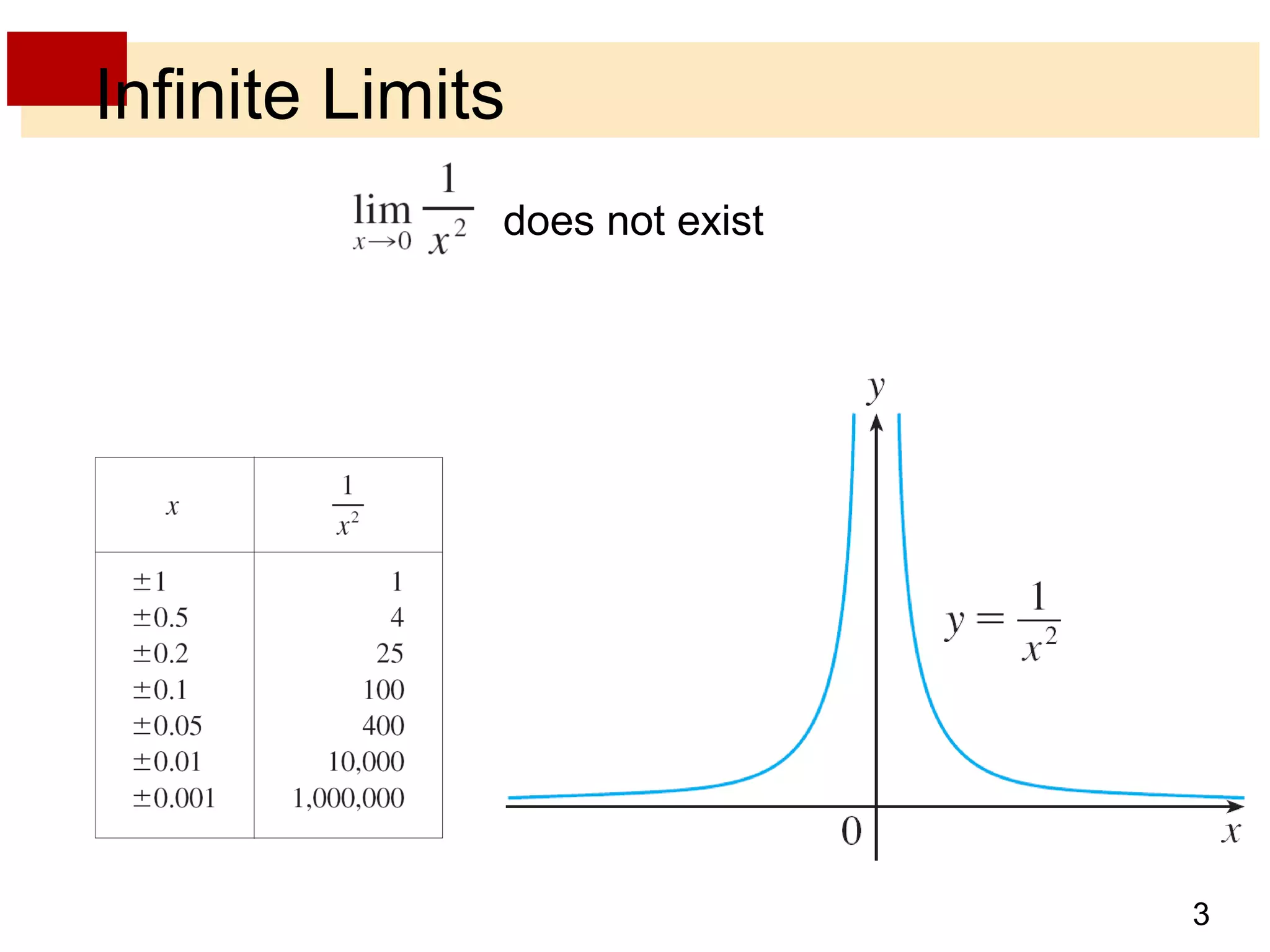
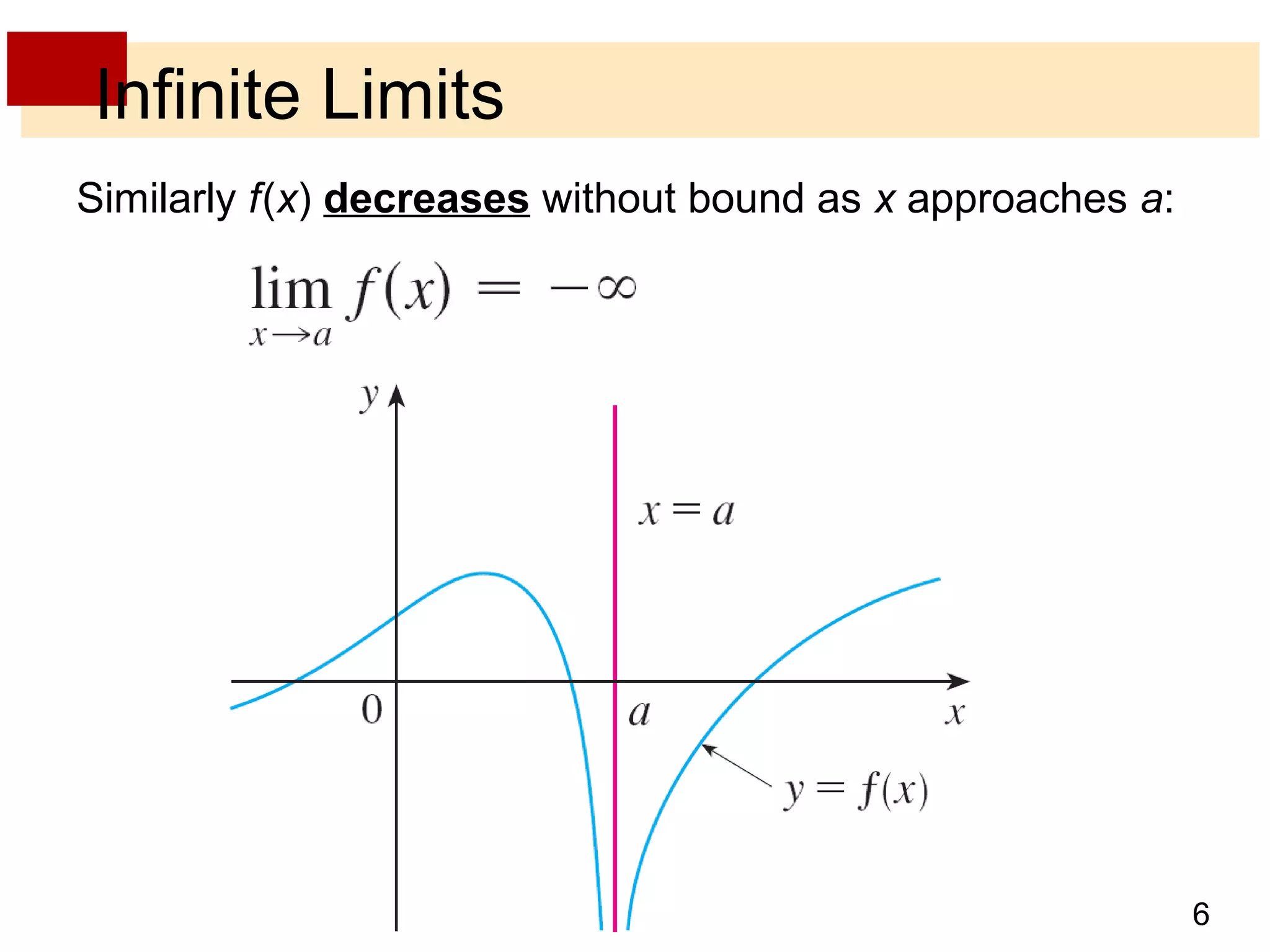
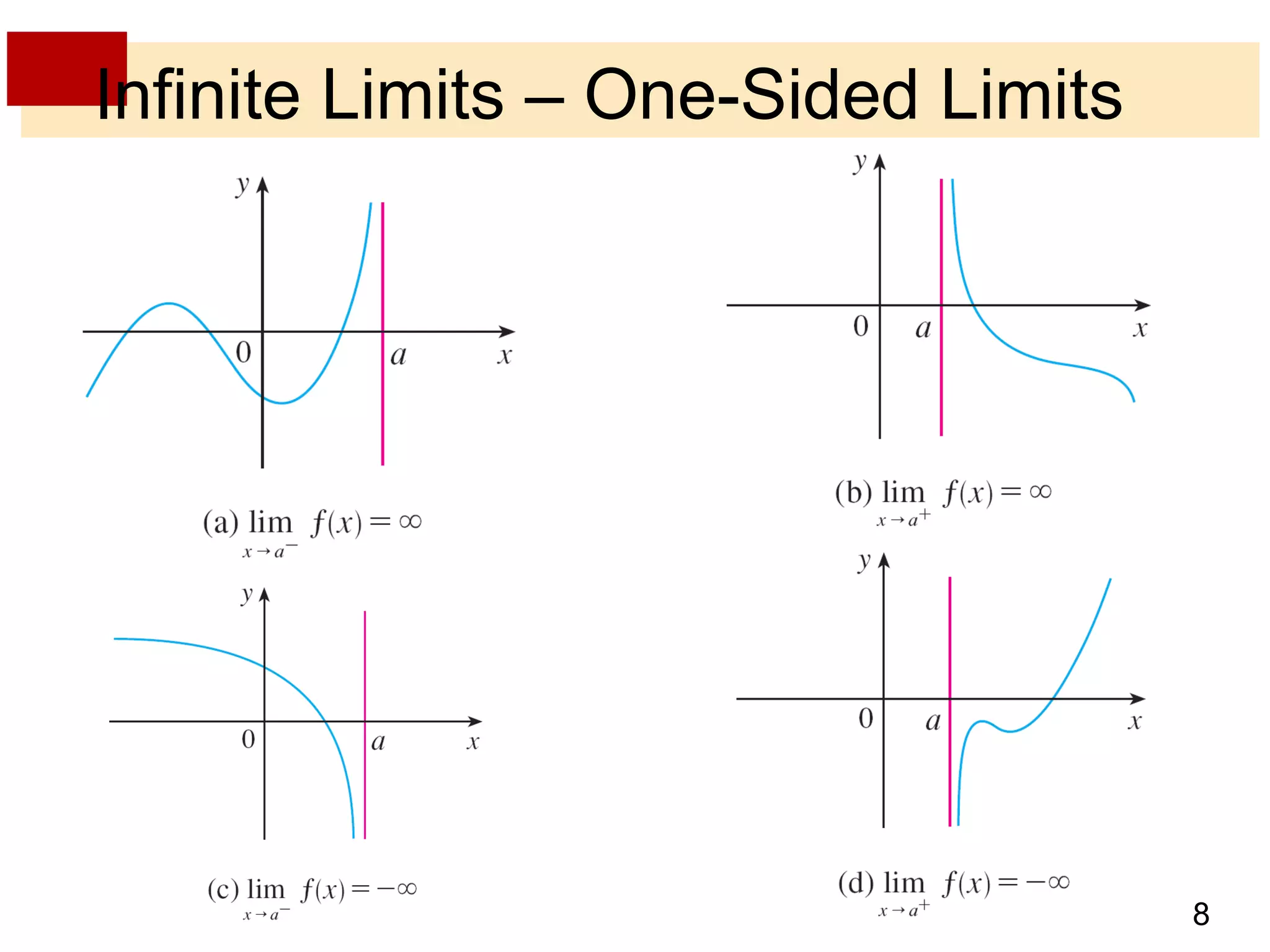
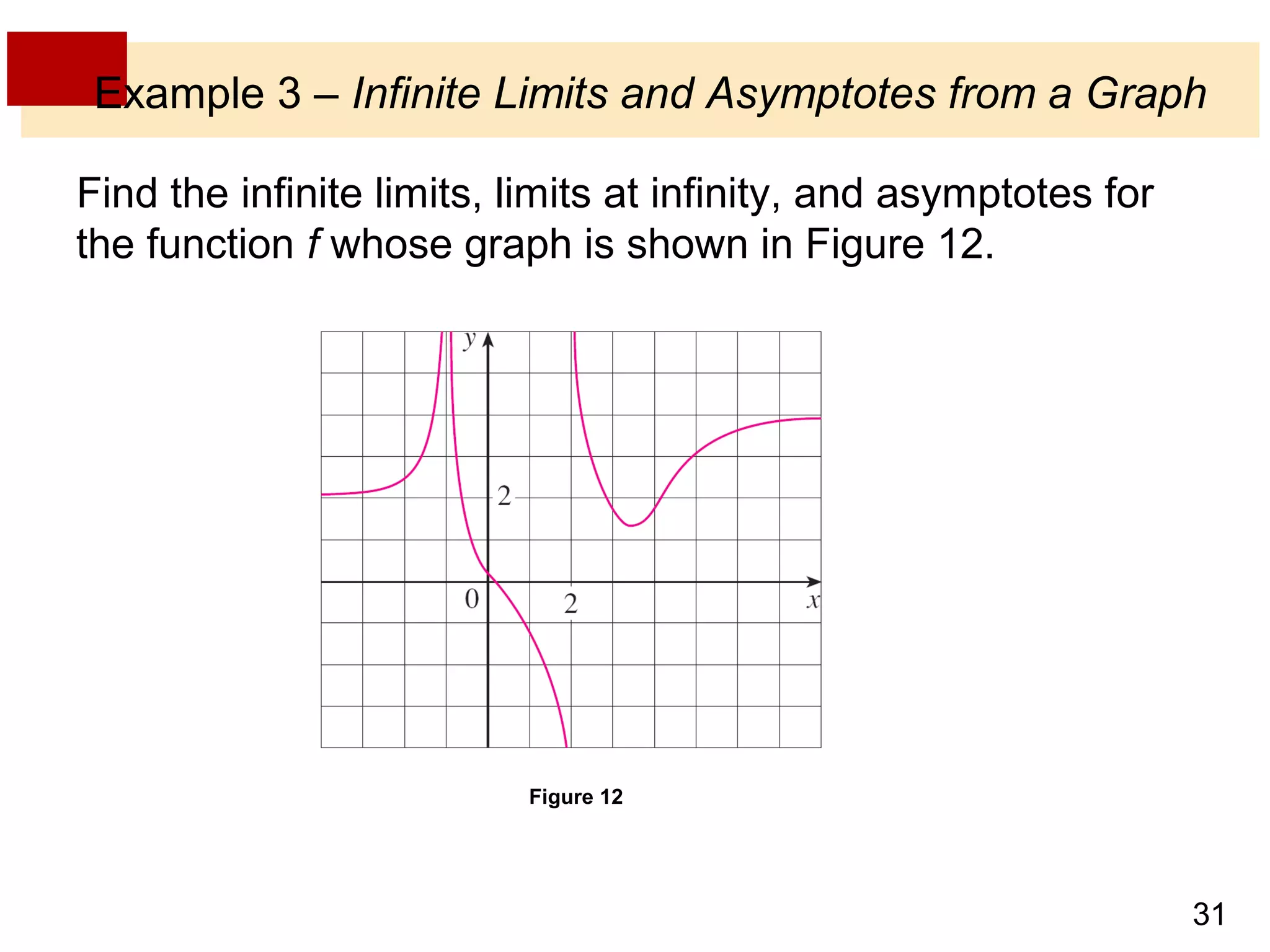
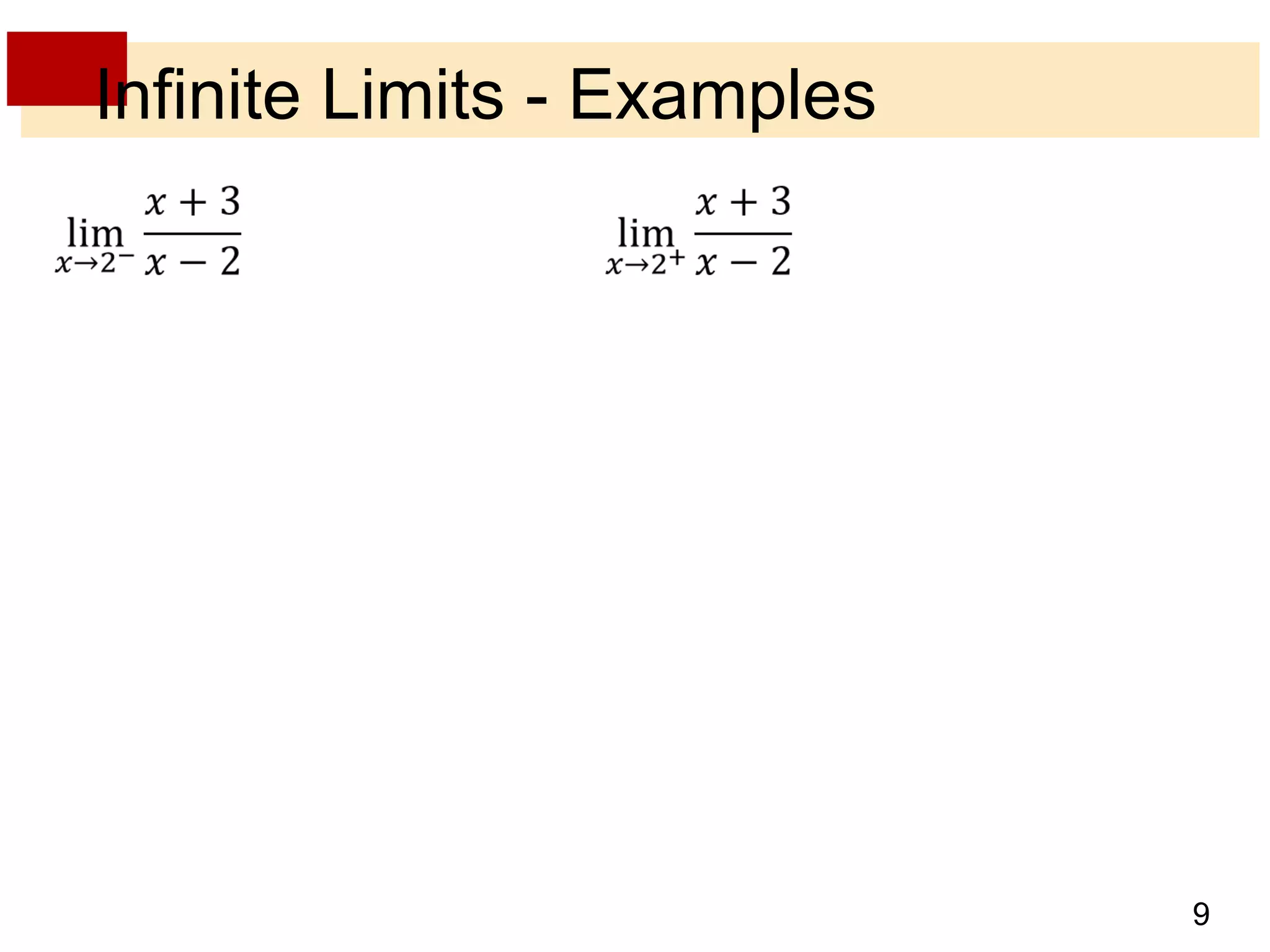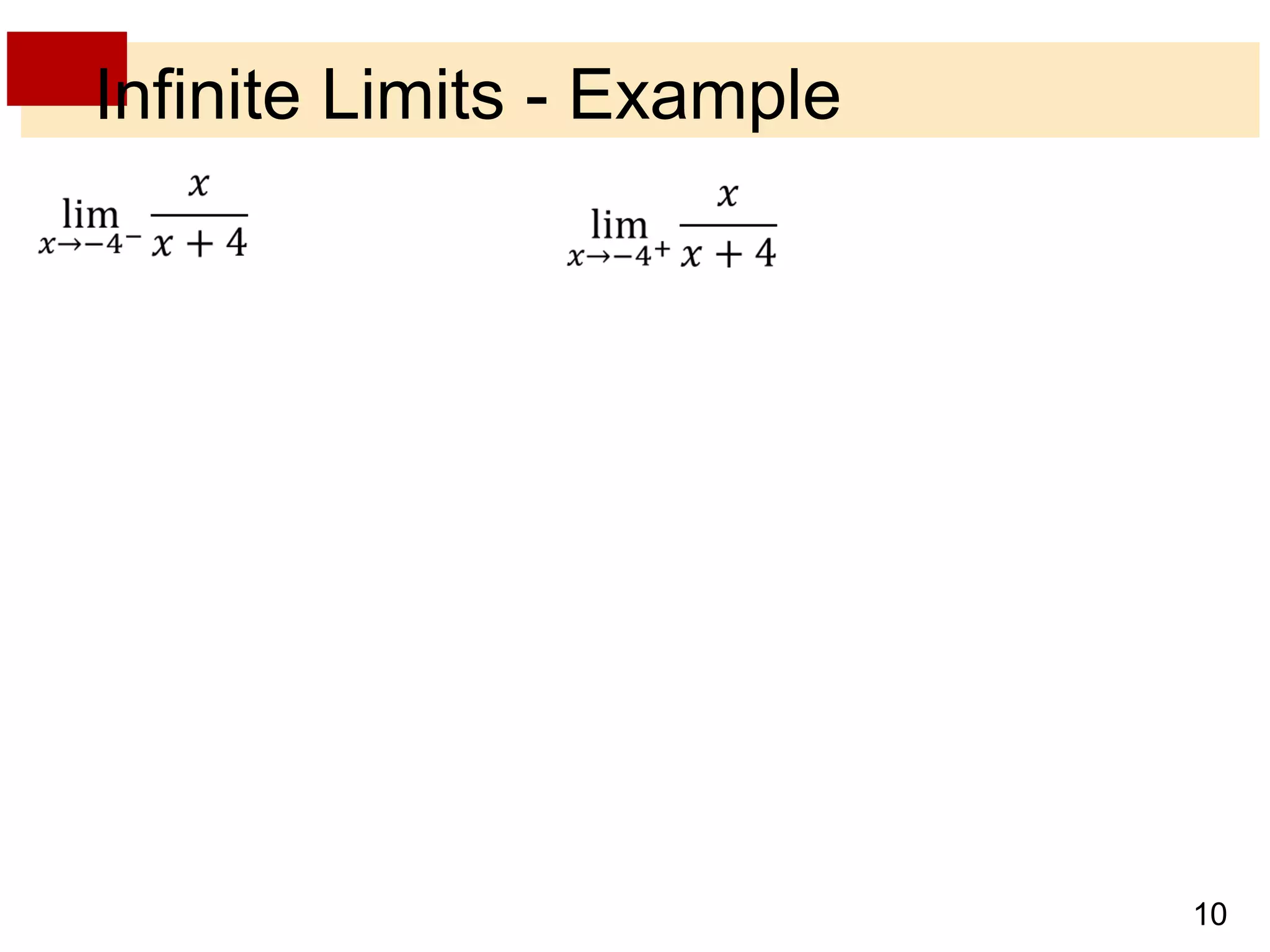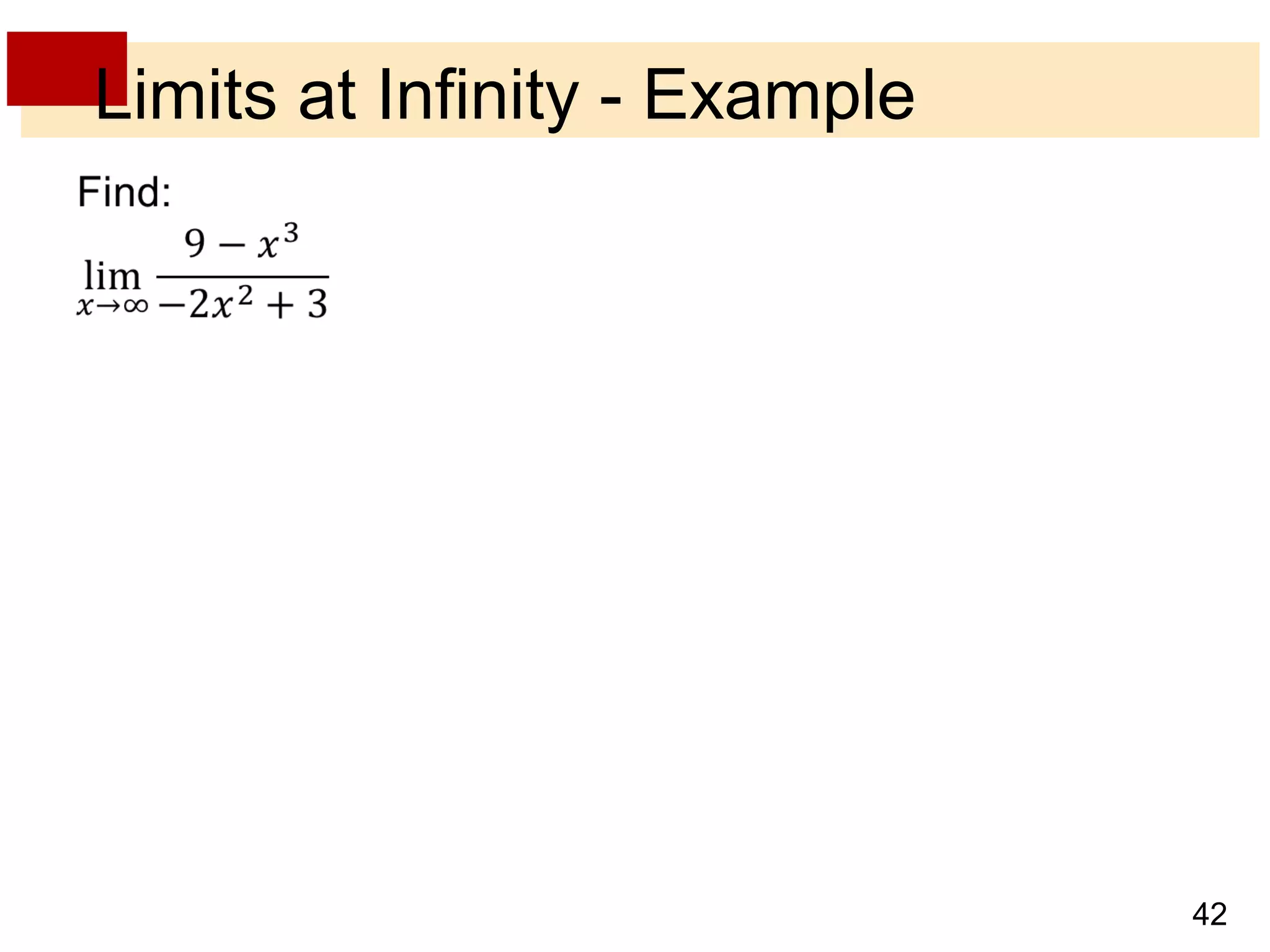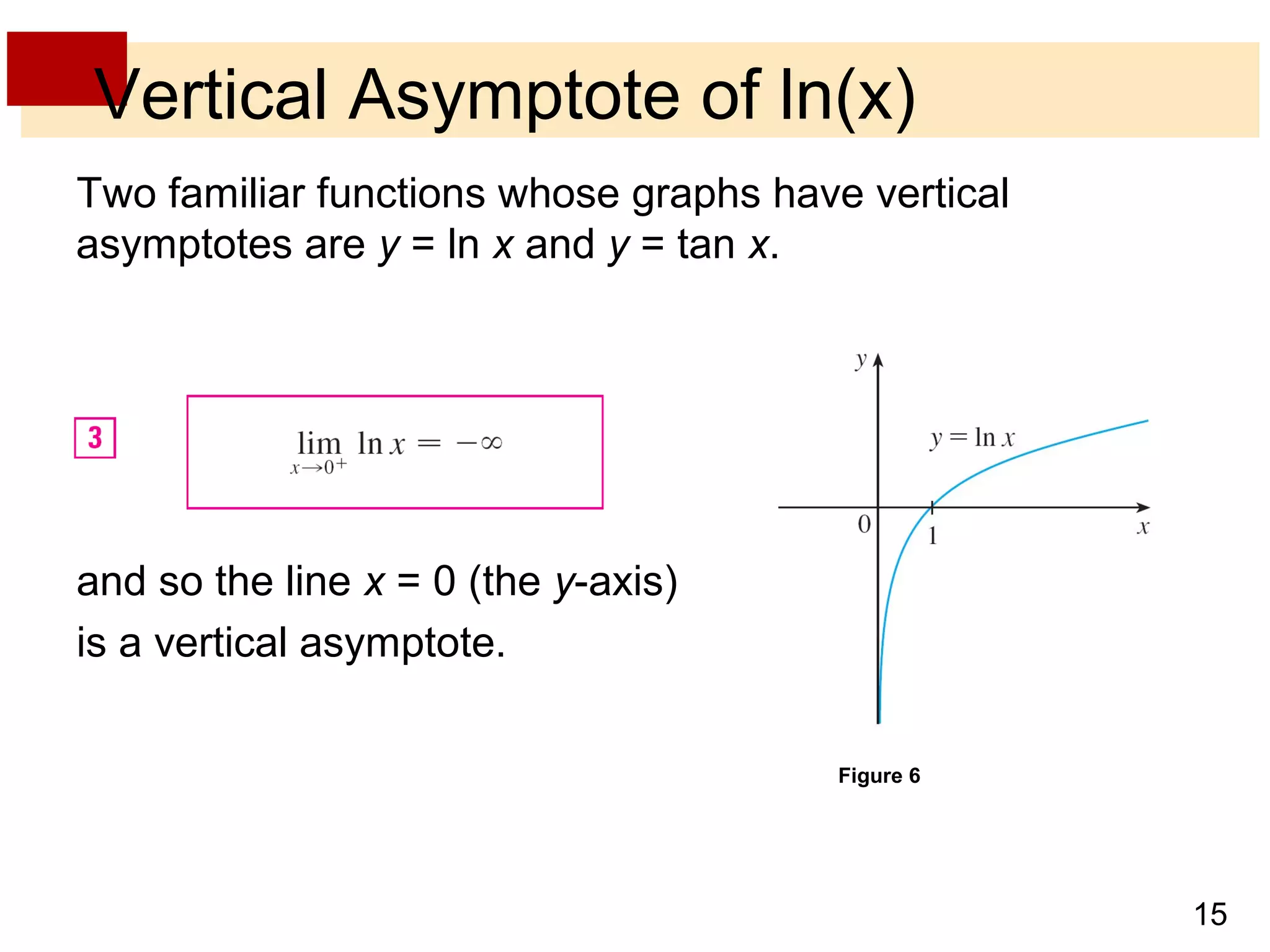
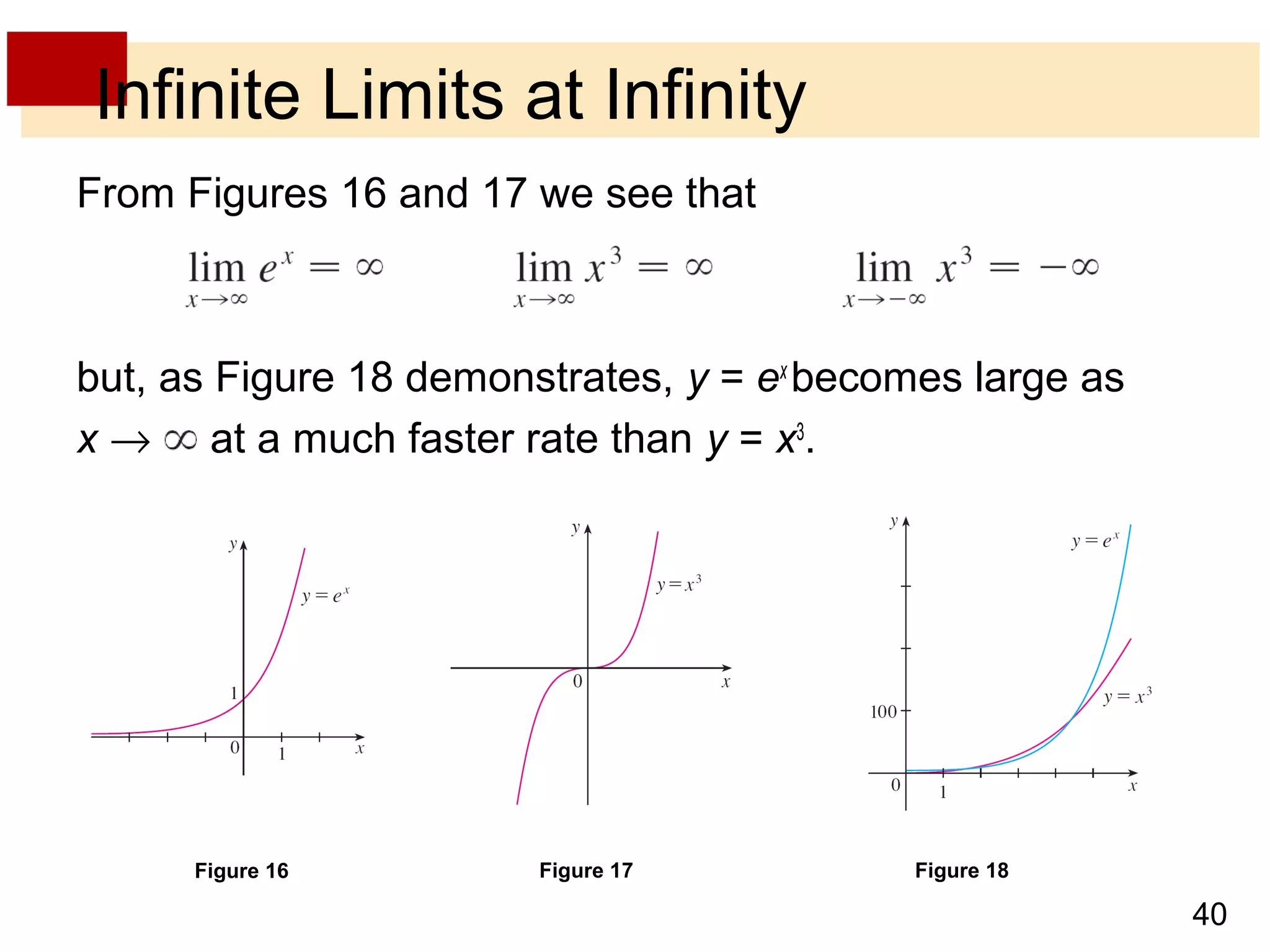
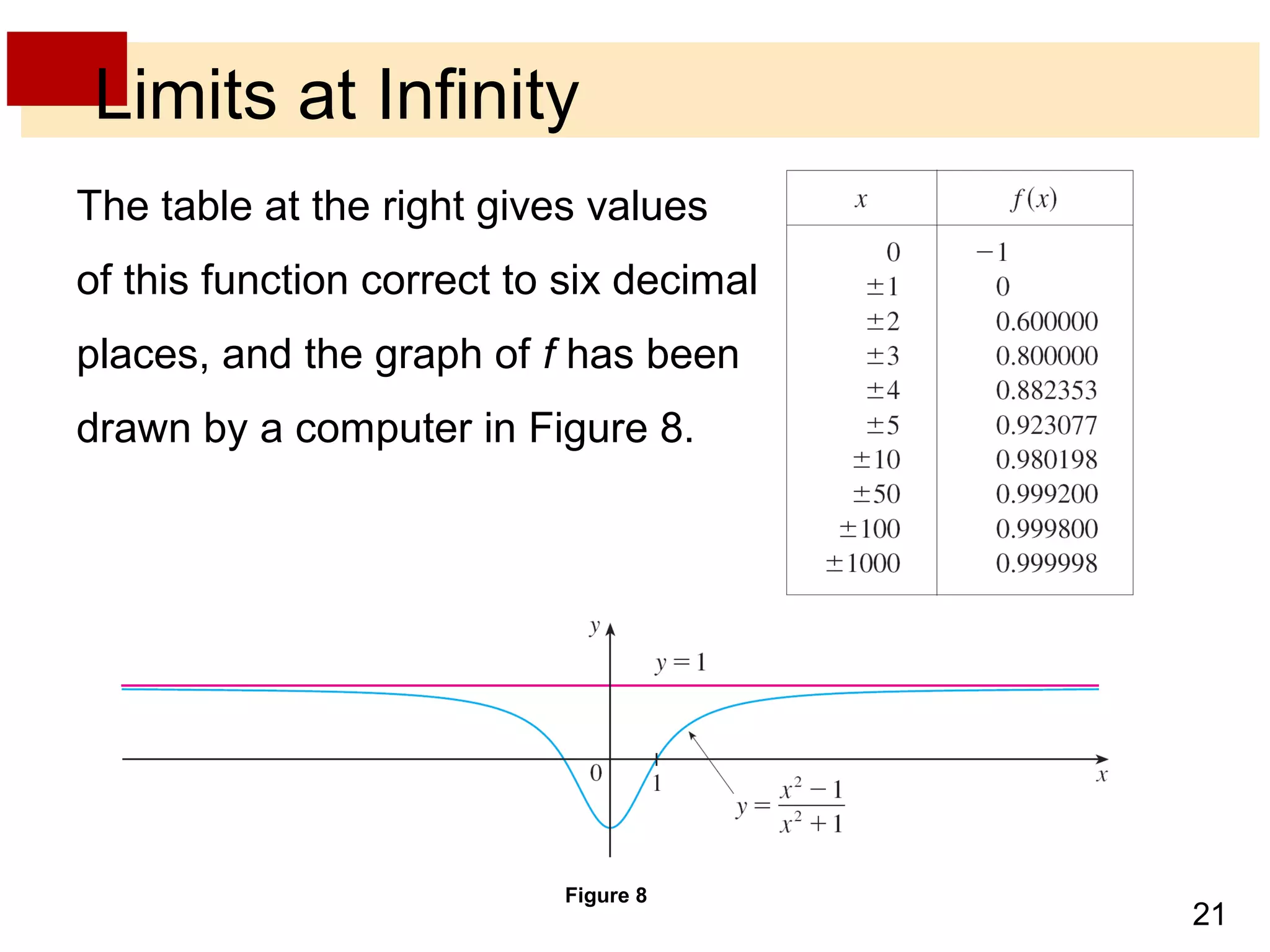
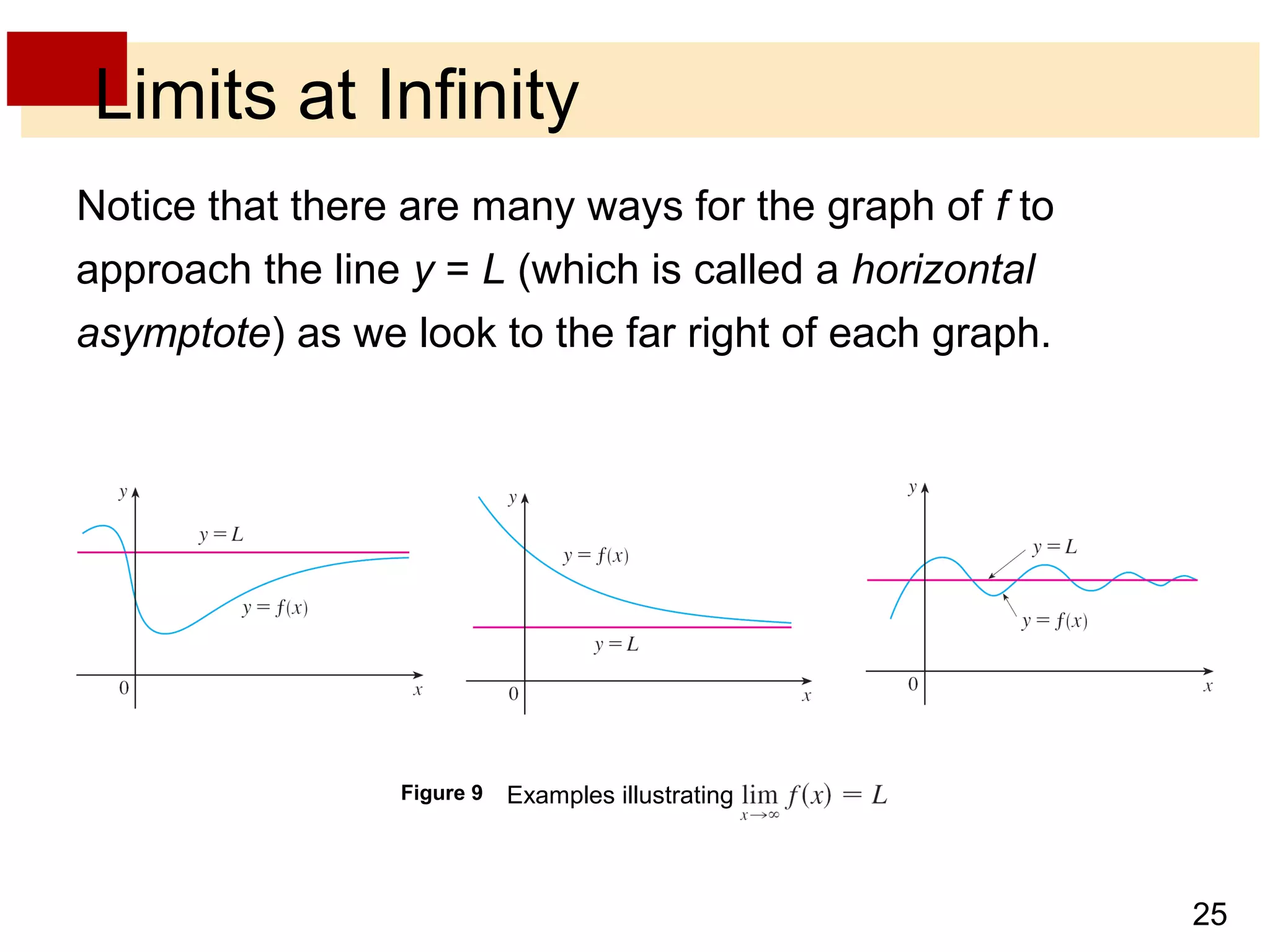
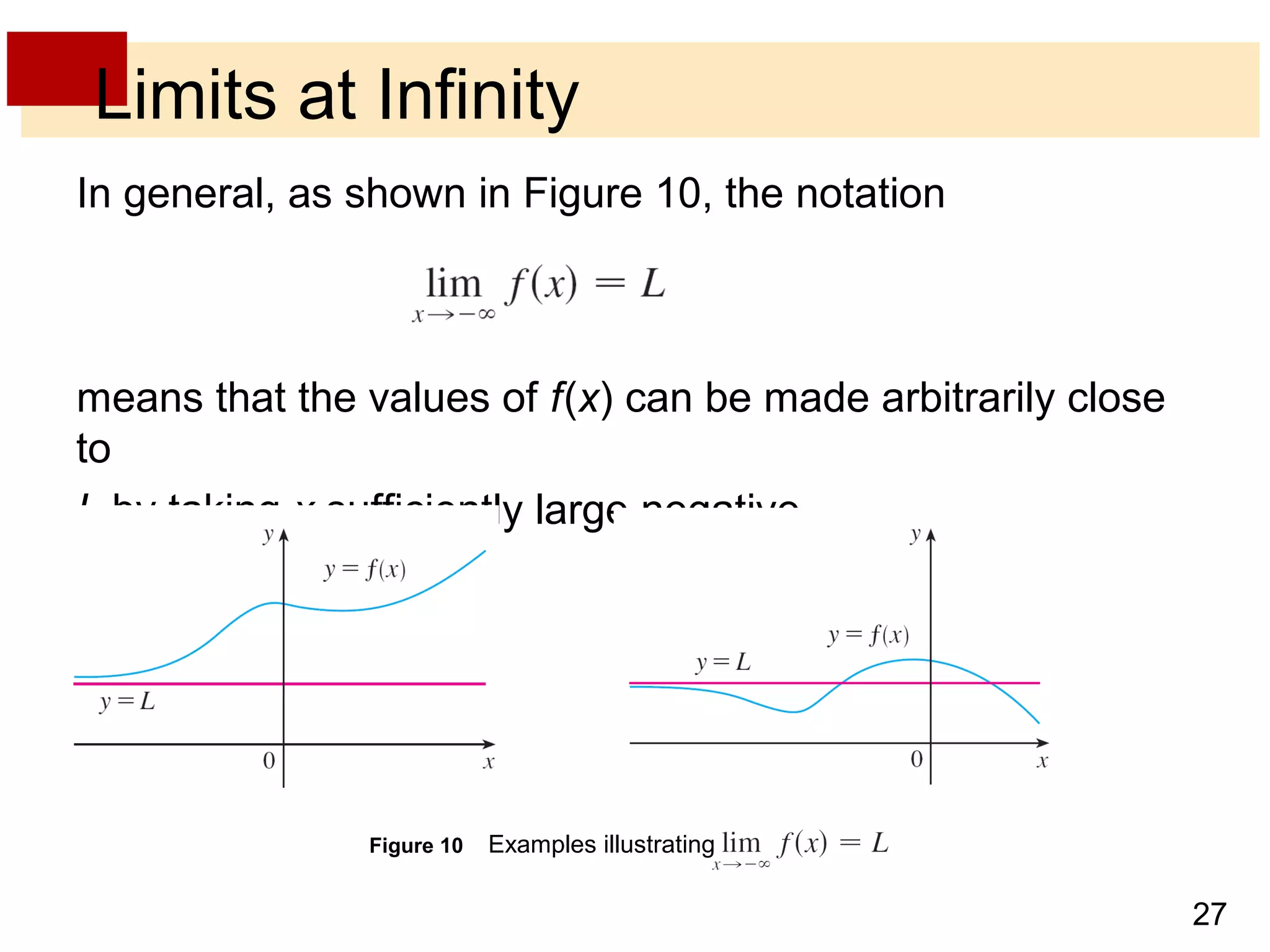
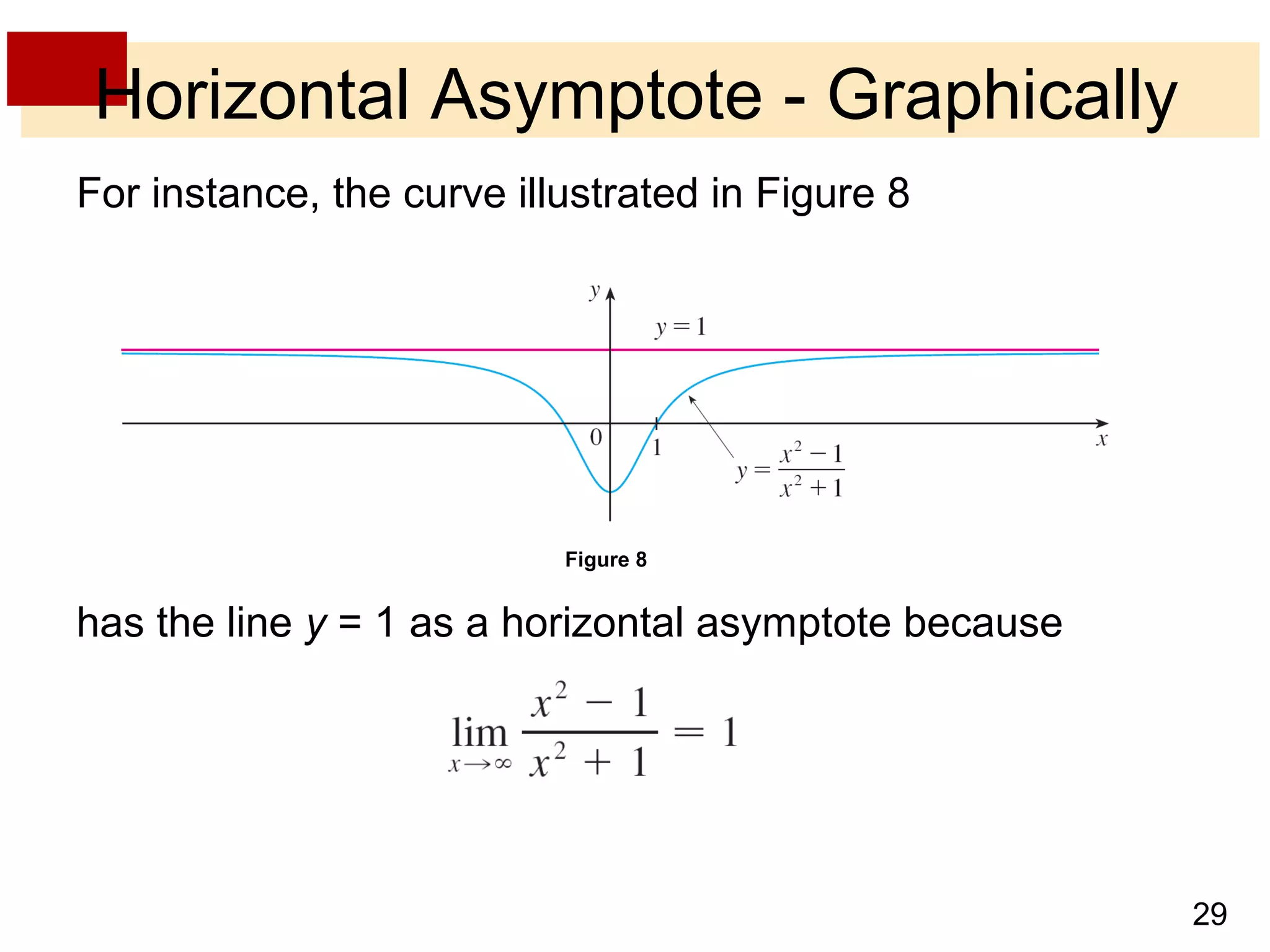
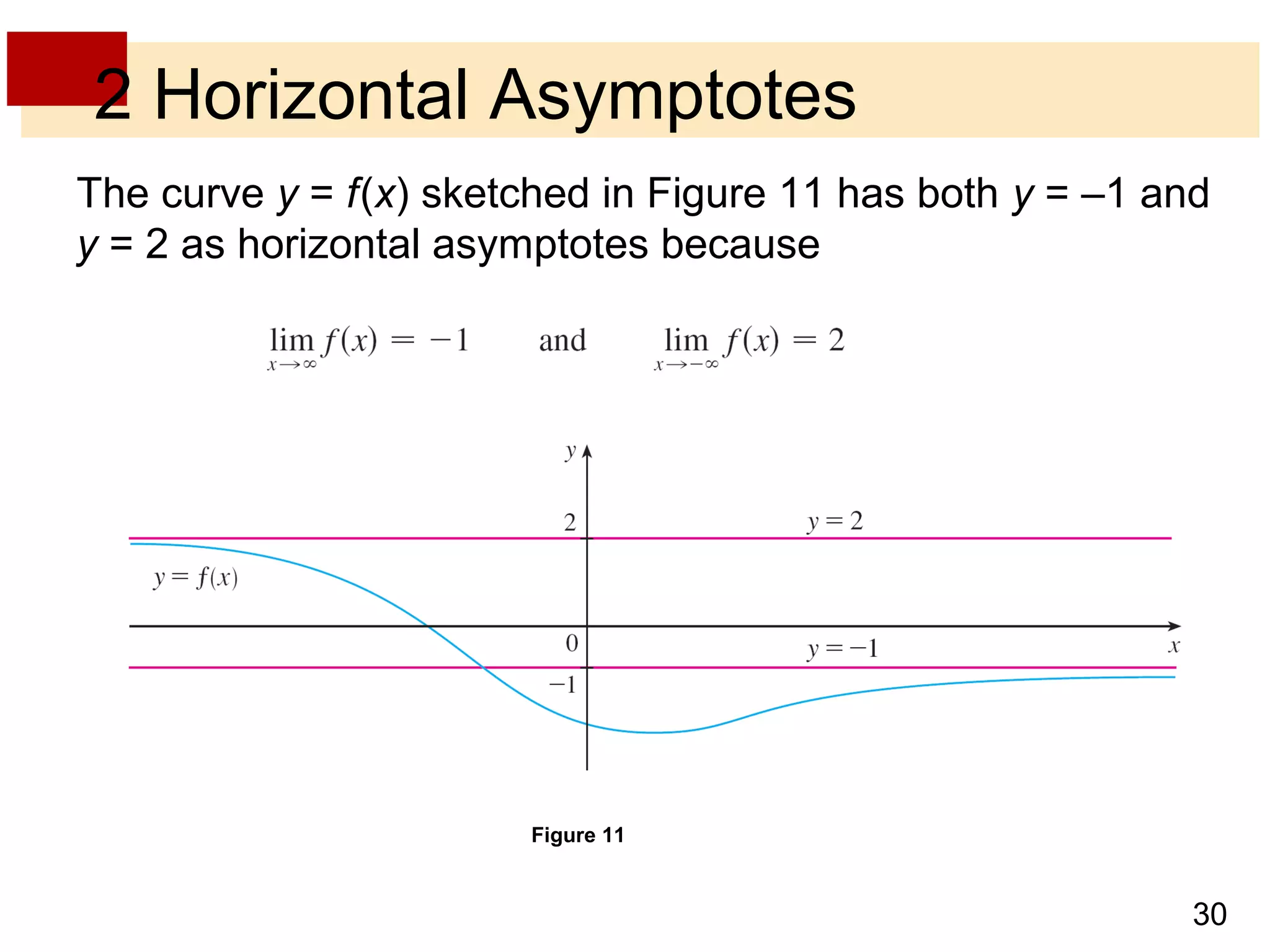
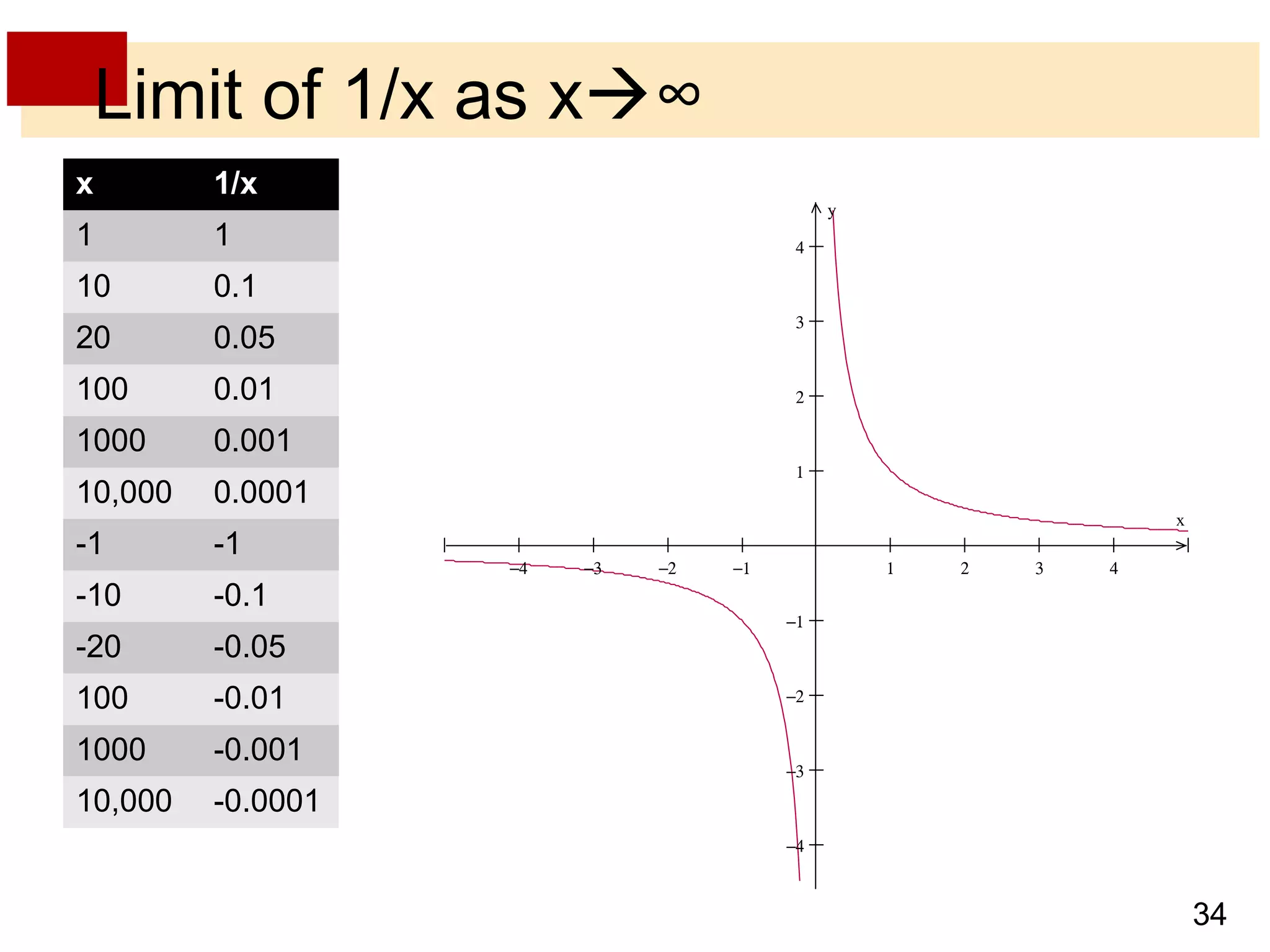
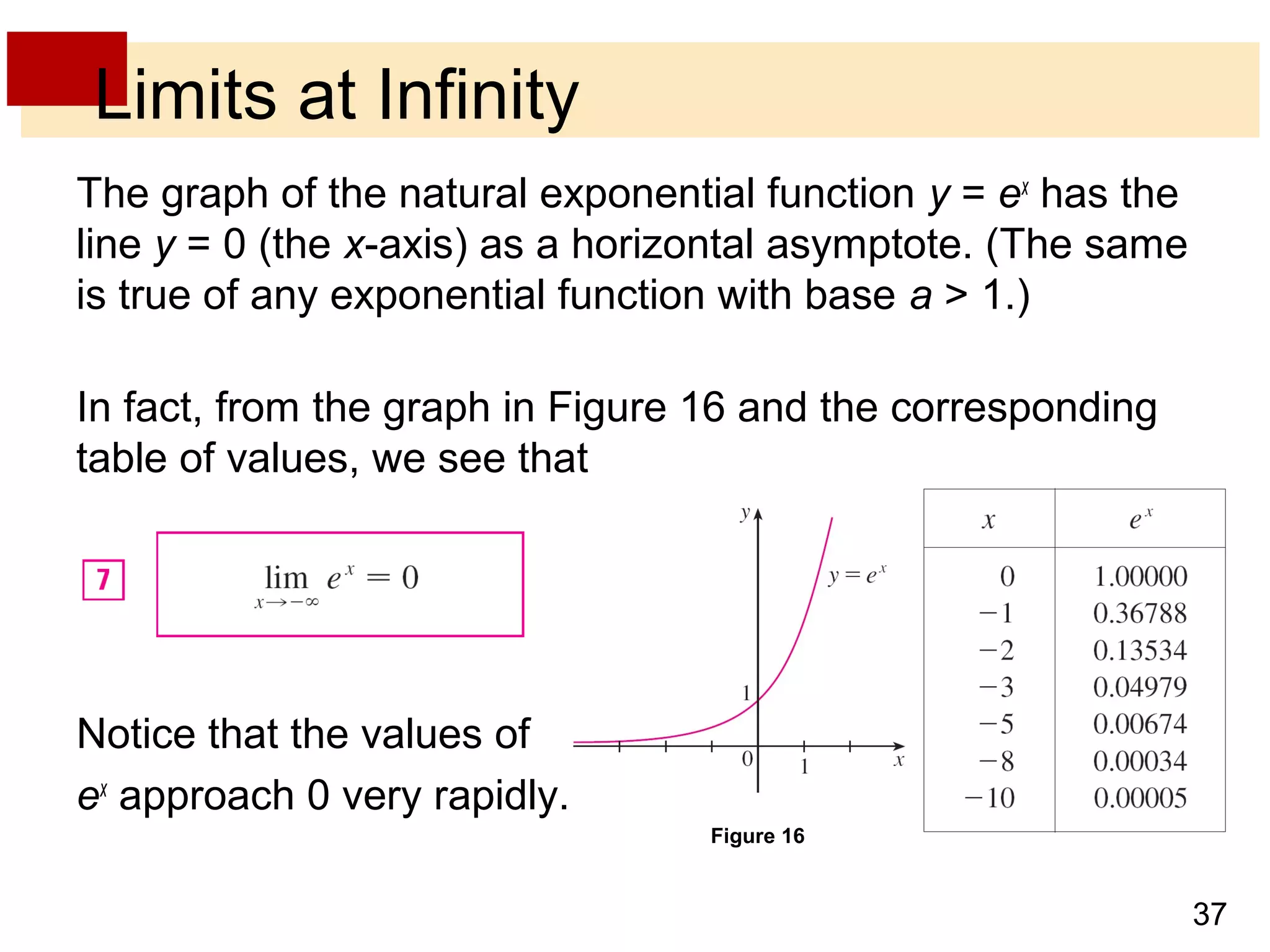
This document discusses limits involving infinity, including infinite limits, limits as x approaches infinity, and limits as x approaches a number. It provides examples and definitions of the following key concepts: - Infinite limits occur when the value of a function increases without bound as x approaches a number, indicated by expressions like limx→a f(x) = ±∞. - Limits at infinity describe the behavior of a function as x becomes arbitrarily large, positive or negative, written as limx→±∞ f(x) = L. If the function values approach a horizontal line L, then L is a horizontal asymptote. 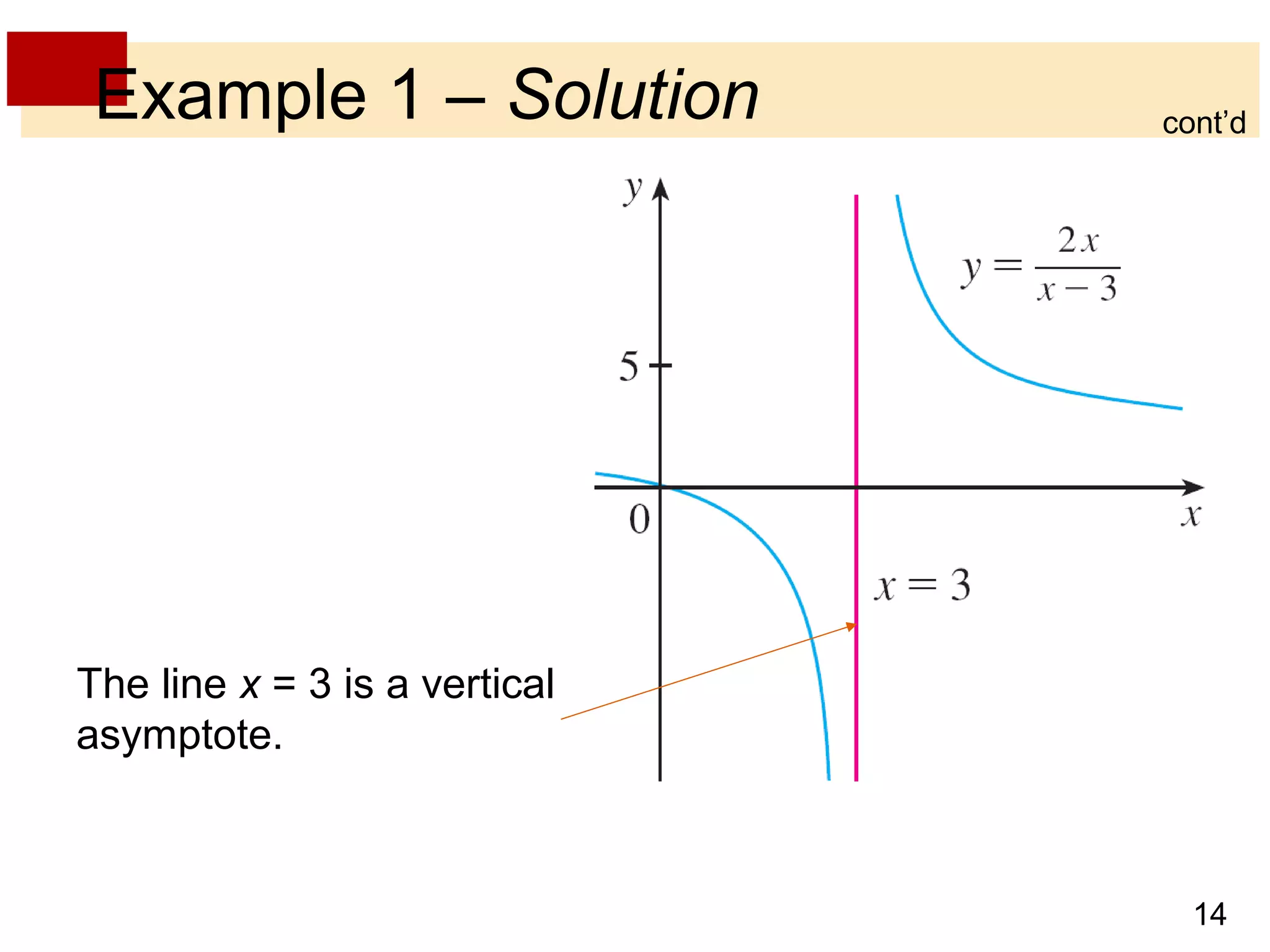- Vertical and horizontal asymptotes describe lines that a function graph approaches

1. Limits 2.5 Involving Infinity

2. 2
Infinite Limits

3. 3
Infinite Limits
does not exist

4. 4
Infinite Limits
As x  0, f(x) gets bigger and bigger without bound
To indicate this kind of behavior we use the notation

5. 5
Infinite Limits
Again, the symbol is not a number, but the expression
limx®a f (x) = is often read as
“the limit of f (x), as x approaches a, is infinity”
or “f (x) becomes infinite as x approaches a”
or “f (x) increases without bound as x approaches
a”
This definition is illustrated
graphically in Figure 2.
Figure 2

6. 6
Infinite Limits
Similarly f (x) decreases without bound as x approaches a:

7. 7
One-Sided Infinite Limits
Similar definitions for the one-sided infinite limits
•“x ® a–” only values of x that are less than a
•“x ® a+” only x > a.

8. 8
Infinite Limits – One-Sided Limits

9. 9
Infinite Limits - Examples

10. 10
Infinite Limits - Example

11. 11
Vertical Asymptotes
For instance, the y-axis is a vertical asymptote of the curve
y = 1/x2 because limx®0 (1/x2) = .
Note: Asymptotes are lines – described by equations
e.g., x = 0

12. Example 1 – Evaluating One-sided Infinite Limits
12
Find and
Solution:
If x is close to 3 but larger than 3, then the denominator
x – 3 is a small positive number and 2x is close to 6.
So the quotient 2x/(x – 3) is a large positive number.
Thus, intuitively, we see that

13. 13
Example 1 – Solution
Likewise, if x is close to 3 but smaller than 3, then x – 3 is a
small negative number but 2x is still a positive number
(close to 6).
So 2x/(x – 3) is a numerically large negative number.
Thus
cont’d

14. 14
Example 1 – Solution
The line x = 3 is a vertical
asymptote.
cont’d

15. 15
Vertical Asymptote of ln(x)
Two familiar functions whose graphs have vertical
asymptotes are y = ln x and y = tan x.
and so the line x = 0 (the y-axis)
is a vertical asymptote.
Figure 6

16. 16
Vertical Asymptotes of tan(x)
and so the line x = p/2 is a vertical asymptote.
In fact, the lines x = (2n + 1)p/2,
n an integer, are all vertical
asymptotes of y = tan x.
Figure 7 y = tan x

17. 17
Vertical Asymptotes - Examples

18. 18
Vertical Asymptote - Example

19. 19
Limits at Infinity

20. 20
Limits at Infinity
Here we let x become arbitrarily large (positive or negative)
and see what happens to y.
Let’s begin by investigating the behavior of the function f
defined by
as x becomes large.

21. 21
Limits at Infinity
The table at the right gives values
of this function correct to six decimal
places, and the graph of f has been
drawn by a computer in Figure 8.
Figure 8

22. 22
Limits at Infinity
As x grows larger and larger you can see that the values of
f (x) get closer and closer to 1.
In fact, it seems that we can make the values of f (x) as close
as we like to 1 by taking x sufficiently large.
This situation is expressed symbolically by writing

23. 23
Limits at Infinity
In general, we use the notation
to indicate that the values of f (x) approach L as x becomes
larger and larger.

24. 24
Limits at Infinity
The symbol does not represent a number.
Nonetheless, the expression is often read as
“the limit of f (x), as x approaches infinity, is L”
or “the limit of f (x), as x becomes infinite, is L”
or “the limit of f (x), as x increases without bound,
is L”

25. 25
Limits at Infinity
Notice that there are many ways for the graph of f to
approach the line y = L (which is called a horizontal
asymptote) as we look to the far right of each graph.
Figure 9 Examples illustrating

26. Limits at Infinity
For numerically large negative values of x, the values of f (x)
are close to 1.
26
Figure 8
By letting x decrease through negative values without
bound, we can make f (x) as close to 1 as we like.
This is expressed by writing

27. 27
Limits at Infinity
In general, as shown in Figure 10, the notation
means that the values of f (x) can be made arbitrarily close
to
L by taking x sufficiently large negative.
Figure 10 Examples illustrating

28. 28
Horizontal Asymptote

29. 29
Horizontal Asymptote - Graphically
For instance, the curve illustrated in Figure 8
Figure 8
has the line y = 1 as a horizontal asymptote because

30. 2 Horizontal Asymptotes
The curve y = f (x) sketched in Figure 11 has both y = –1 and
y = 2 as horizontal asymptotes because
30
Figure 11

31. Example 3 – Infinite Limits and Asymptotes from a Graph
Find the infinite limits, limits at infinity, and asymptotes for
the function f whose graph is shown in Figure 12.
31
Figure 12

32. Example 3 – Solution
We see that the values of f (x) become large as x ® –1 from
both sides, so
32
Notice that f (x) becomes large negative as x approaches 2
from the left, but large positive as x approaches 2 from the
right. So
Thus both of the lines x = –1 and x = 2 are vertical
asymptotes.

33. 33
Example 3 – Solution
As x becomes large, it appears that f (x) approaches 4.
But as x decreases through negative values, f (x)
approaches 2. So
This means that both y = 4 and y = 2 are horizontal
asymptotes.
cont’d

34. 34
Limit of 1/x as x∞
x 1/x
1 1
10 0.1
20 0.05
100 0.01
1000 0.001
10,000 0.0001
-1 -1
-10 -0.1
-20 -0.05
100 -0.01
1000 -0.001
10,000 -0.0001
4
3
2
1
-4 -3 -2 -1 1 2 3 4
-1
-2
-3
-4
x
y

35. 35
Limits at Infinity
Most of the Limit Laws hold for limits at infinity. It can be
proved that the Limit Laws are also valid if “x ® a” is
replaced by “x ® ” or “x ® .”
In particular, we obtain the following important rule for
calculating limits.

36. 36
Limits at Infinitely - Algebraically
Divide each term by highest power of x in denominator:
Examples:

37. 37
Limits at Infinity
The graph of the natural exponential function y = ex has the
line y = 0 (the x-axis) as a horizontal asymptote. (The same
is true of any exponential function with base a > 1.)
In fact, from the graph in Figure 16 and the corresponding
table of values, we see that
Notice that the values of
ex approach 0 very rapidly.
Figure 16

38. 38
Infinite Limits at Infinity

39. 39
Infinite Limits at Infinity
The notation
is used to indicate that the values of f (x) become large as
x becomes large.
Similar meanings are attached to the following symbols:

40. 40
Infinite Limits at Infinity
From Figures 16 and 17 we see that
but, as Figure 18 demonstrates, y = ex becomes large as
x ® at a much faster rate than y = x3.
Figure 16 Figure 17 Figure 18

41. 41
Limits at Infinity Examples

42. 42
Limits at Infinity - Example