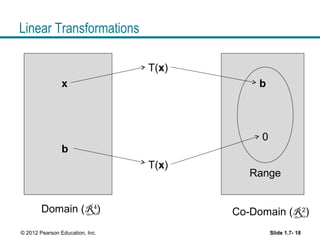
This document discusses linear independence and linear transformations. It defines linear independence of vectors and vector sets and provides examples to illustrate the concept. Key results covered include: a set of vectors is linearly dependent if one vector can be written as a linear combination of the others; a set with more vectors than dimensions is linearly dependent; and a set containing the zero vector is linearly dependent. The document also defines linear transformations and matrix transformations, and discusses properties such as whether a transformation is one-to-one or onto based on the matrix.



![Slide 1.7- 4© 2012 Pearson Education, Inc.
LINEAR INDEPENDENCE OF MATRIX COLUMNS
matrix A = [a1a2 … a3]
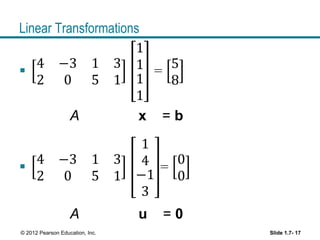
The matrix equation Ax = 0 can be written as
x1v1 + x1v1+ …+ x1v1 = 0
Each linear dependence relation among the columns of
A corresponds to a nontrivial solution of Ax = 0.
Thus, the columns of matrix A are linearly independent
iff the equation Ax = 0 has only the trivial solution.](https://image.slidesharecdn.com/lecture3-section1-71-8and1-9-150204151721-conversion-gate02/85/Lecture-3-section-1-7-1-8-and-1-9-4-320.jpg)



















![How to Find Matrix of Transformation
Theorem 10: T: Rn
Rm
is linear
transformation, then a unique matrix A such
that T(x) = Ax for all x in Rn
A is mxn whose jth
column is the vector T(ej) where ej
is the jth
column of In
A = [T(e1) … T(en)]
Examine 1 point in each direction!!
Slide 1.7- 26© 2012 Pearson Education, Inc.](https://image.slidesharecdn.com/lecture3-section1-71-8and1-9-150204151721-conversion-gate02/85/Lecture-3-section-1-7-1-8-and-1-9-26-320.jpg)



