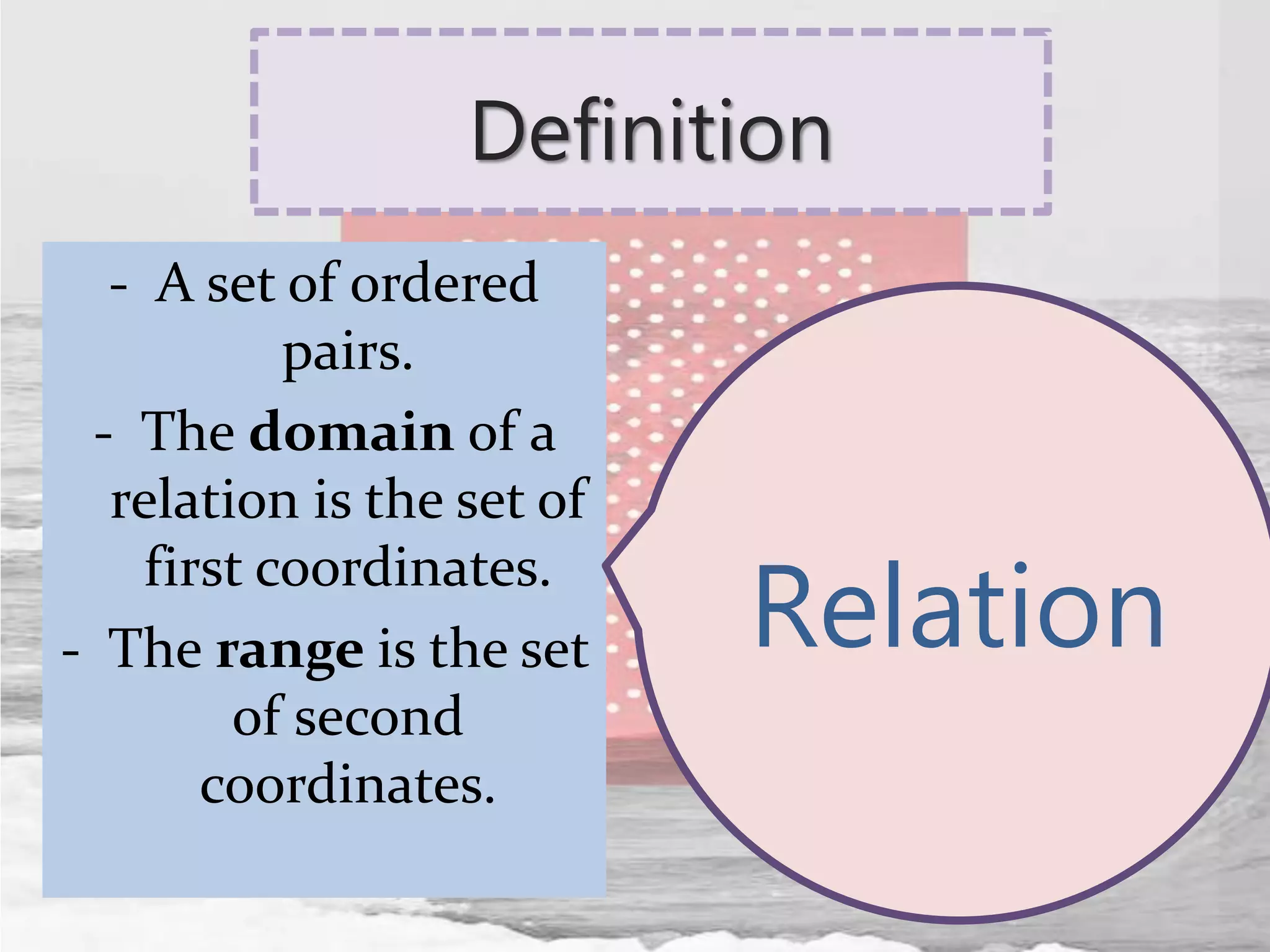
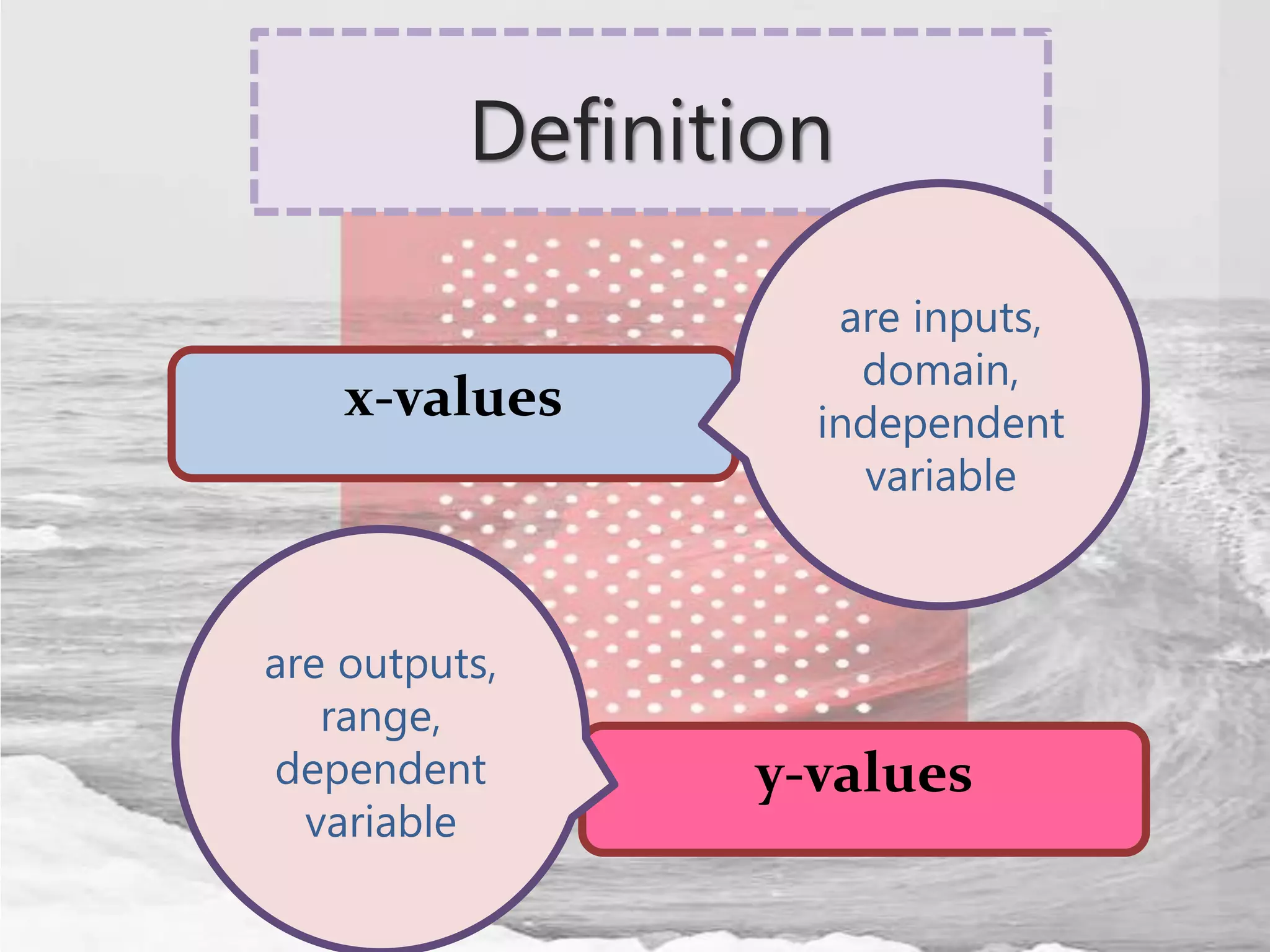
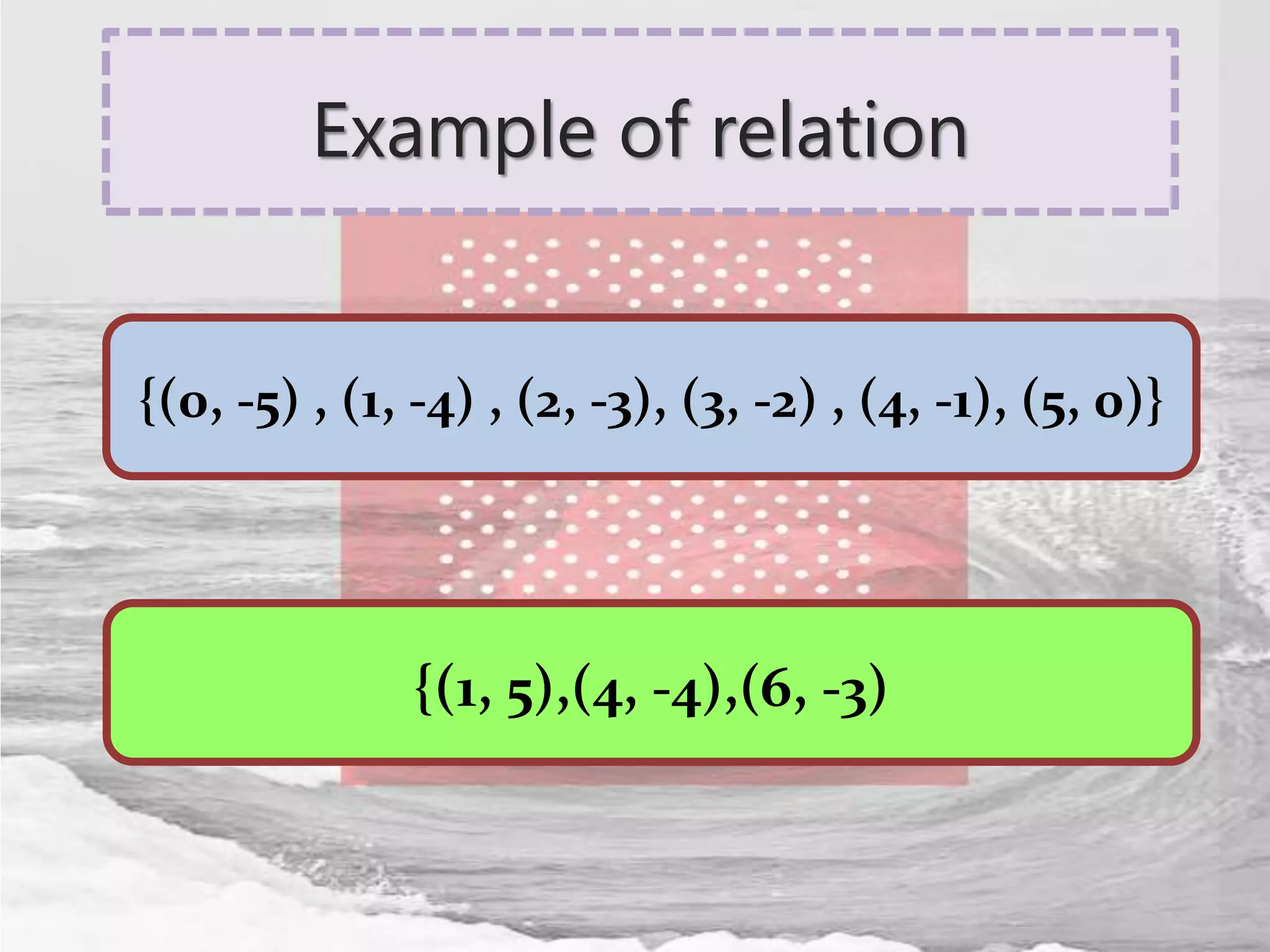
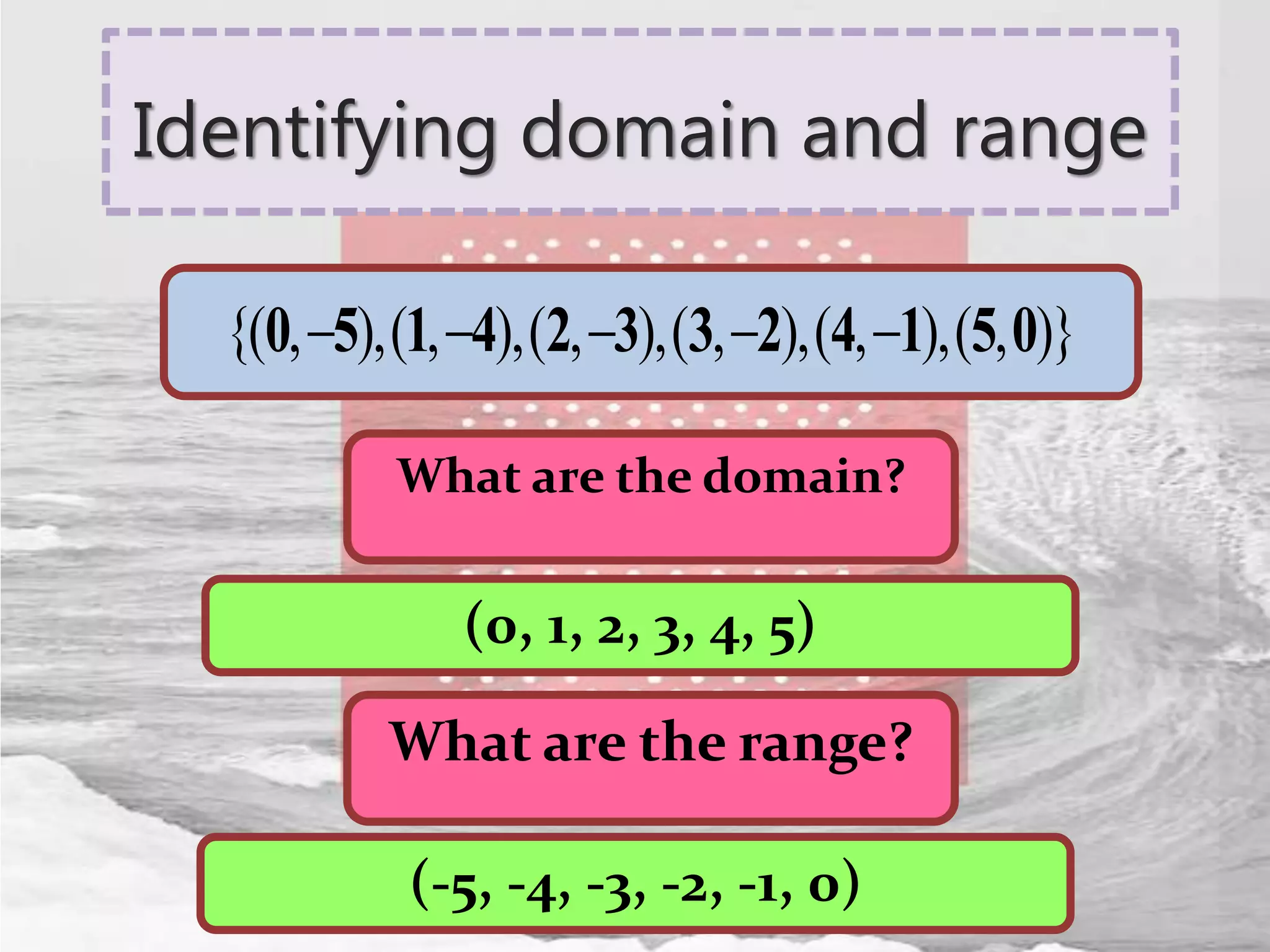
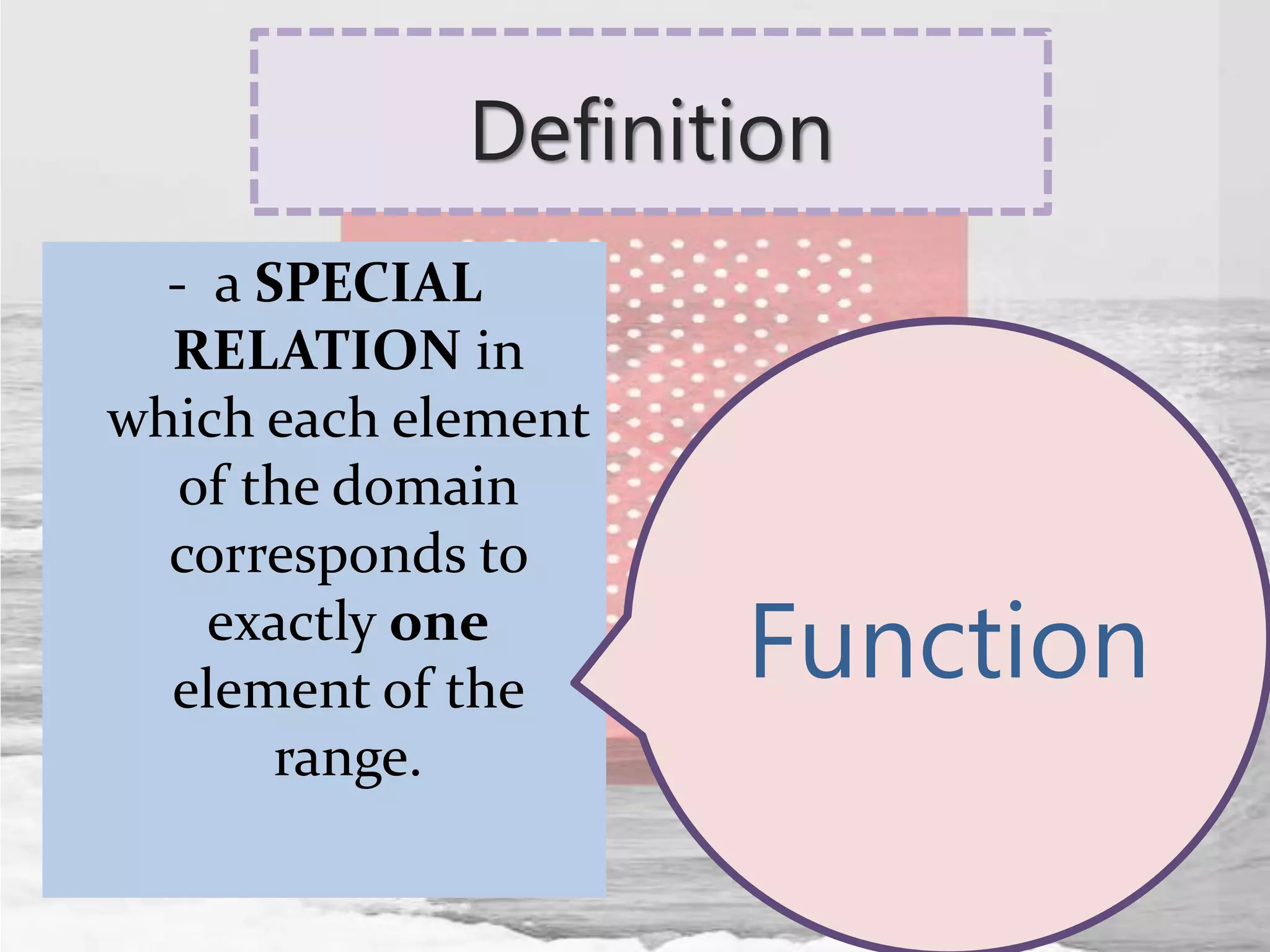
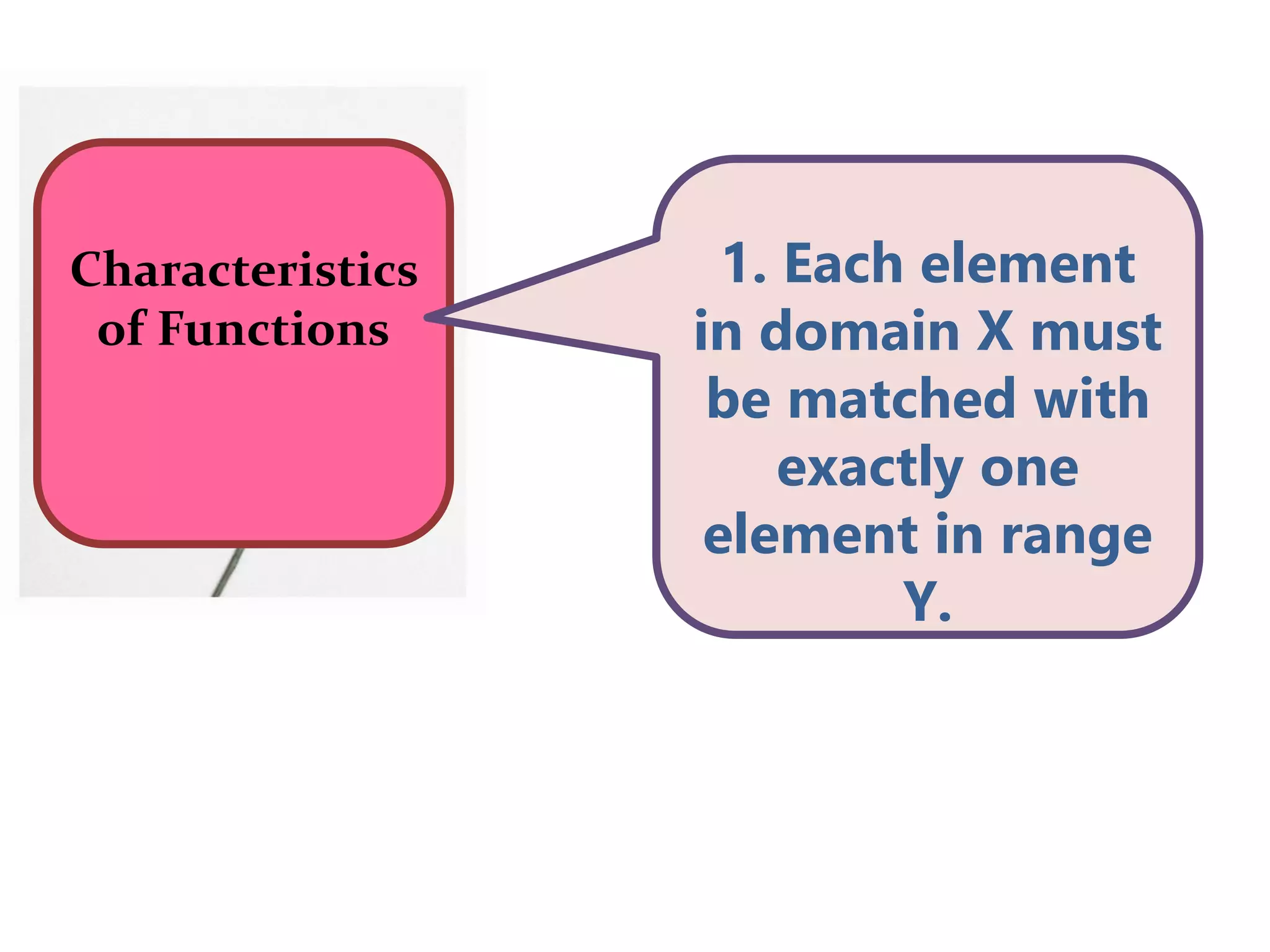
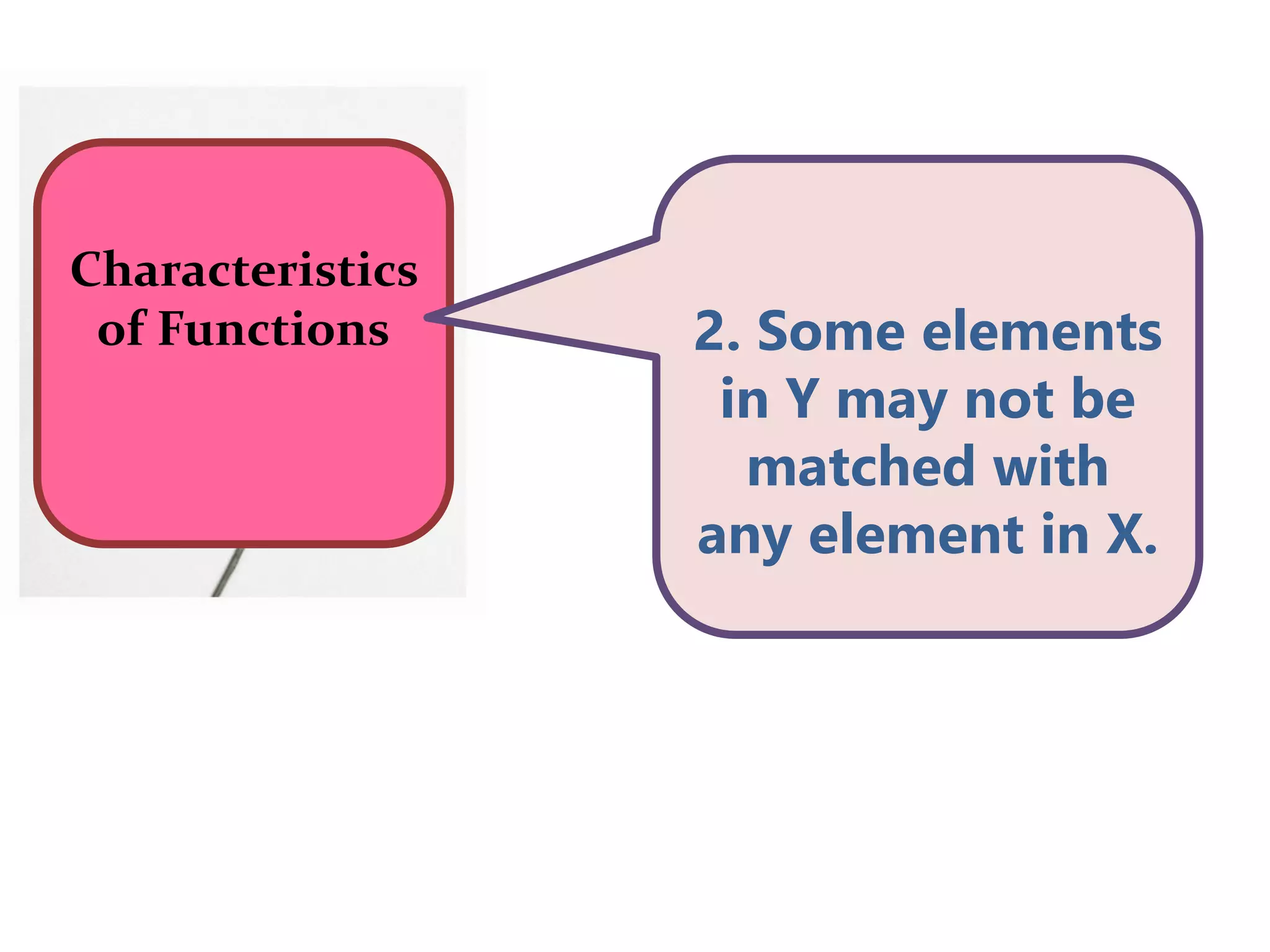
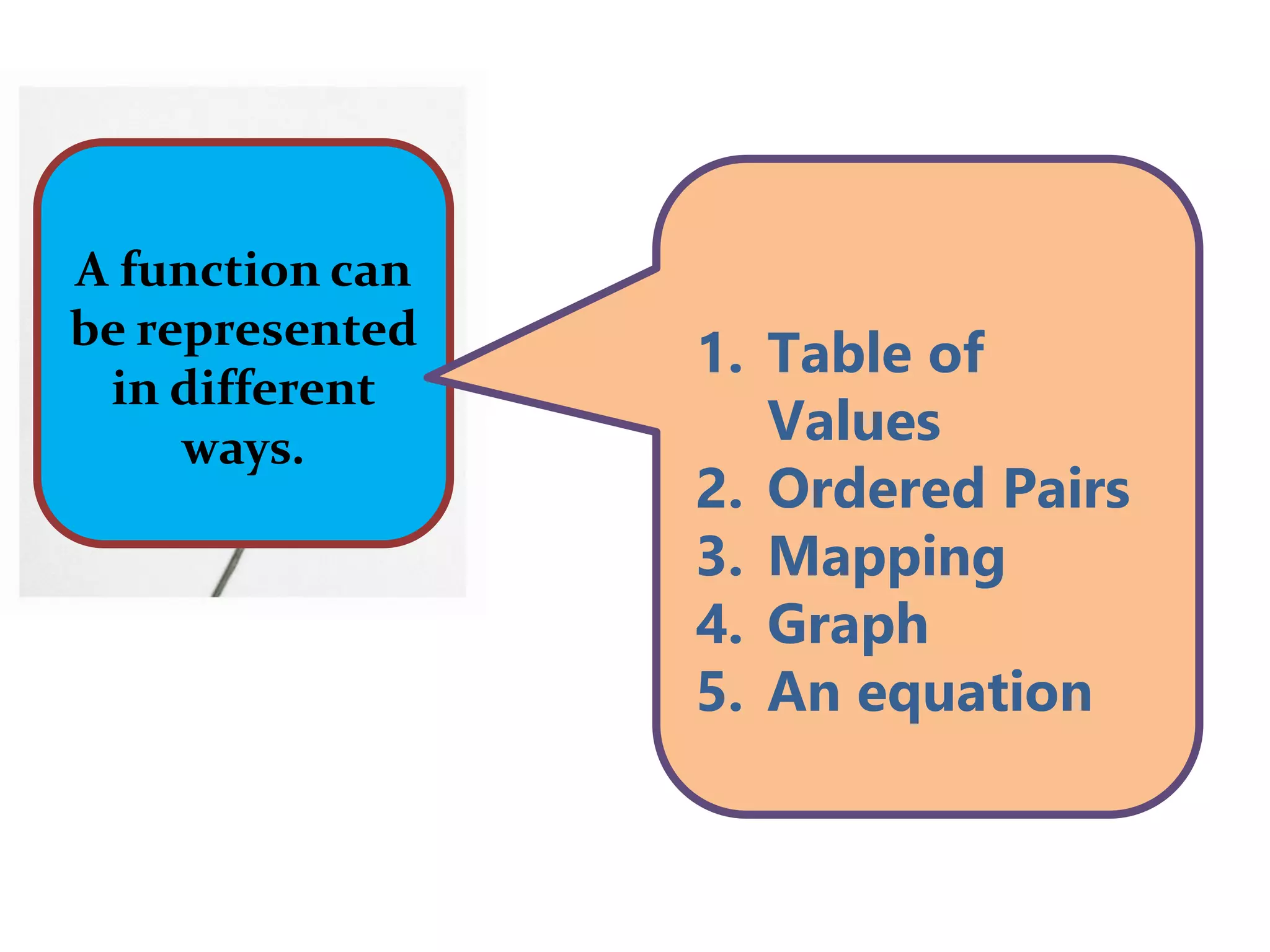
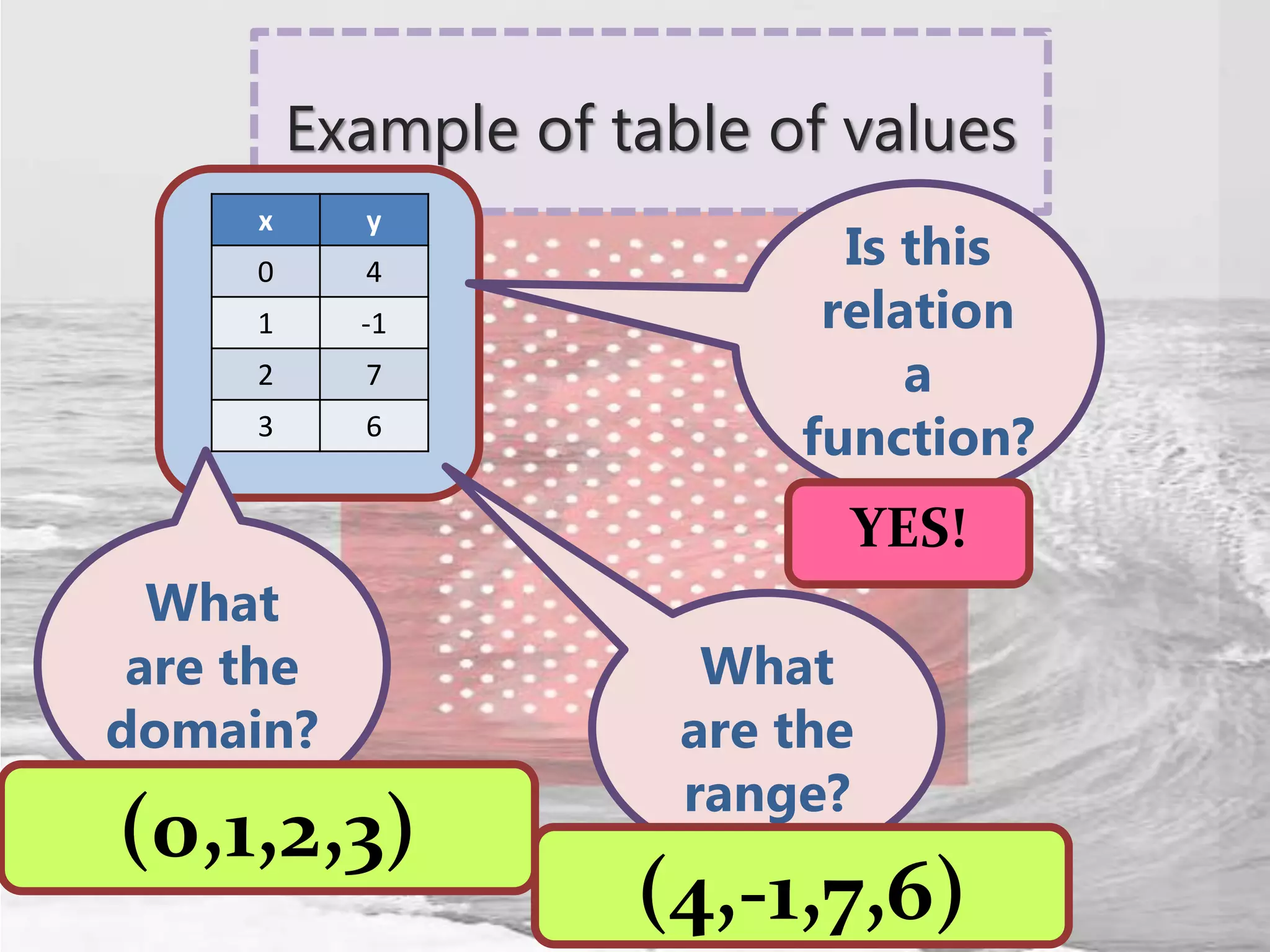
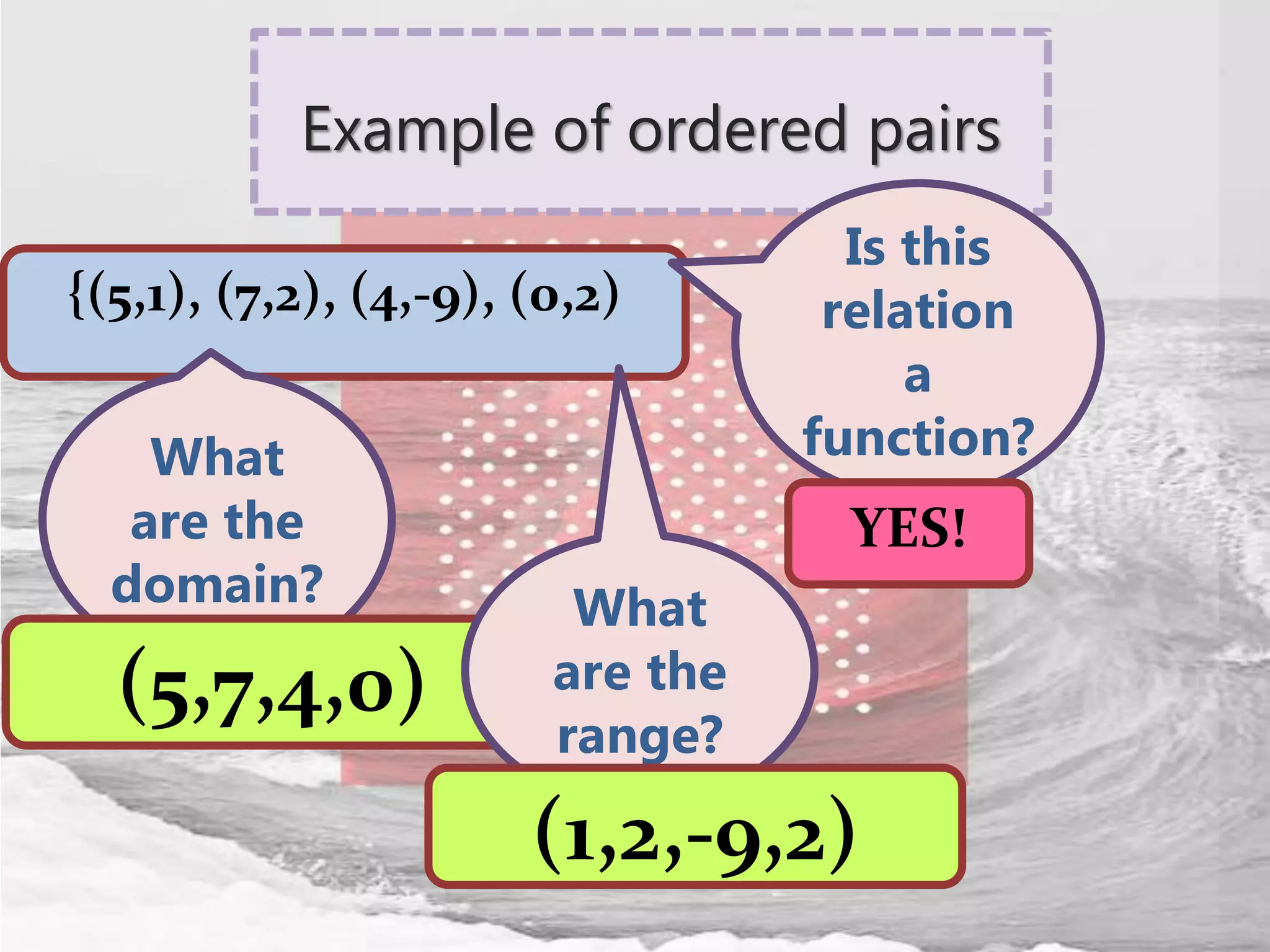
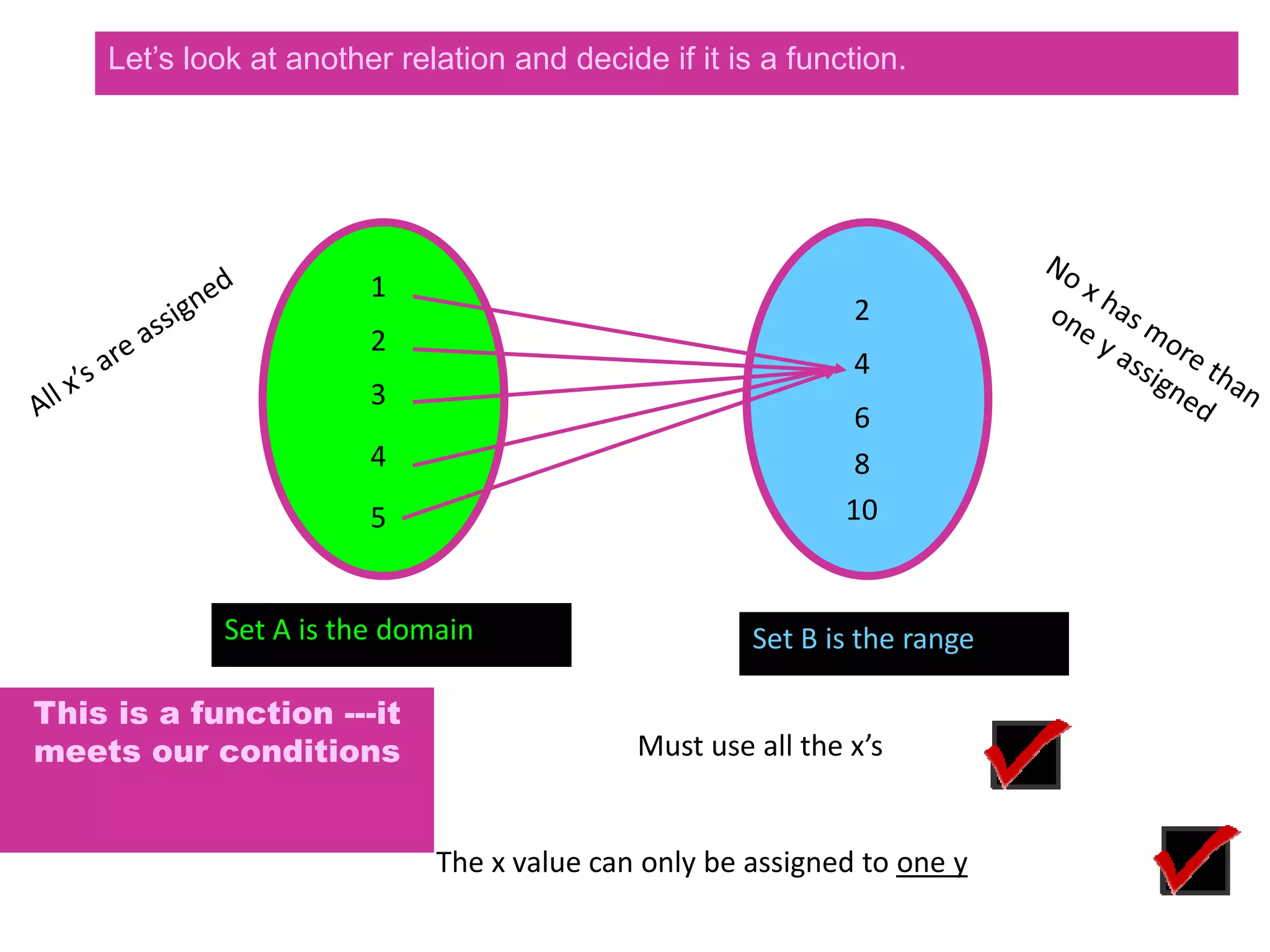
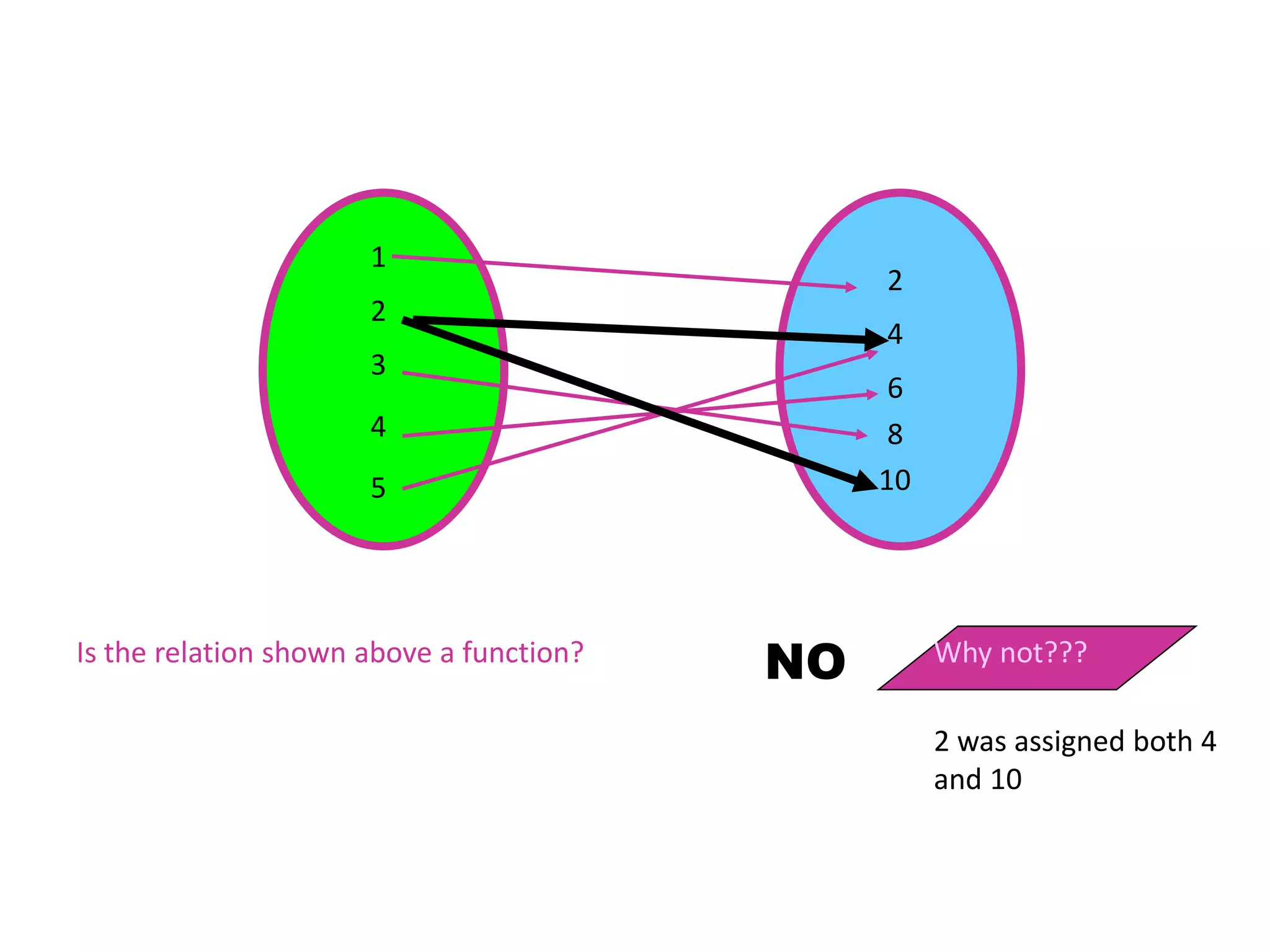
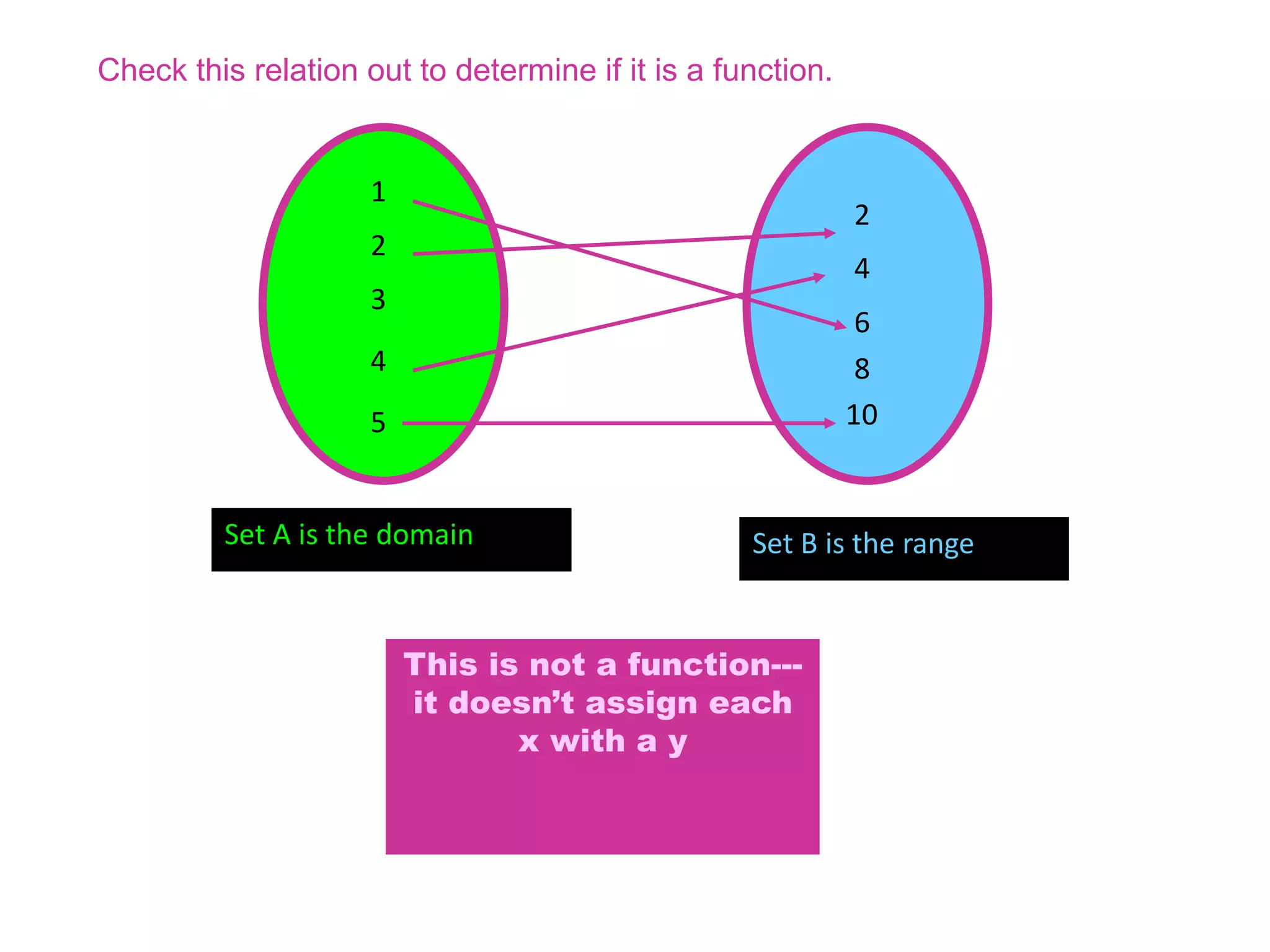
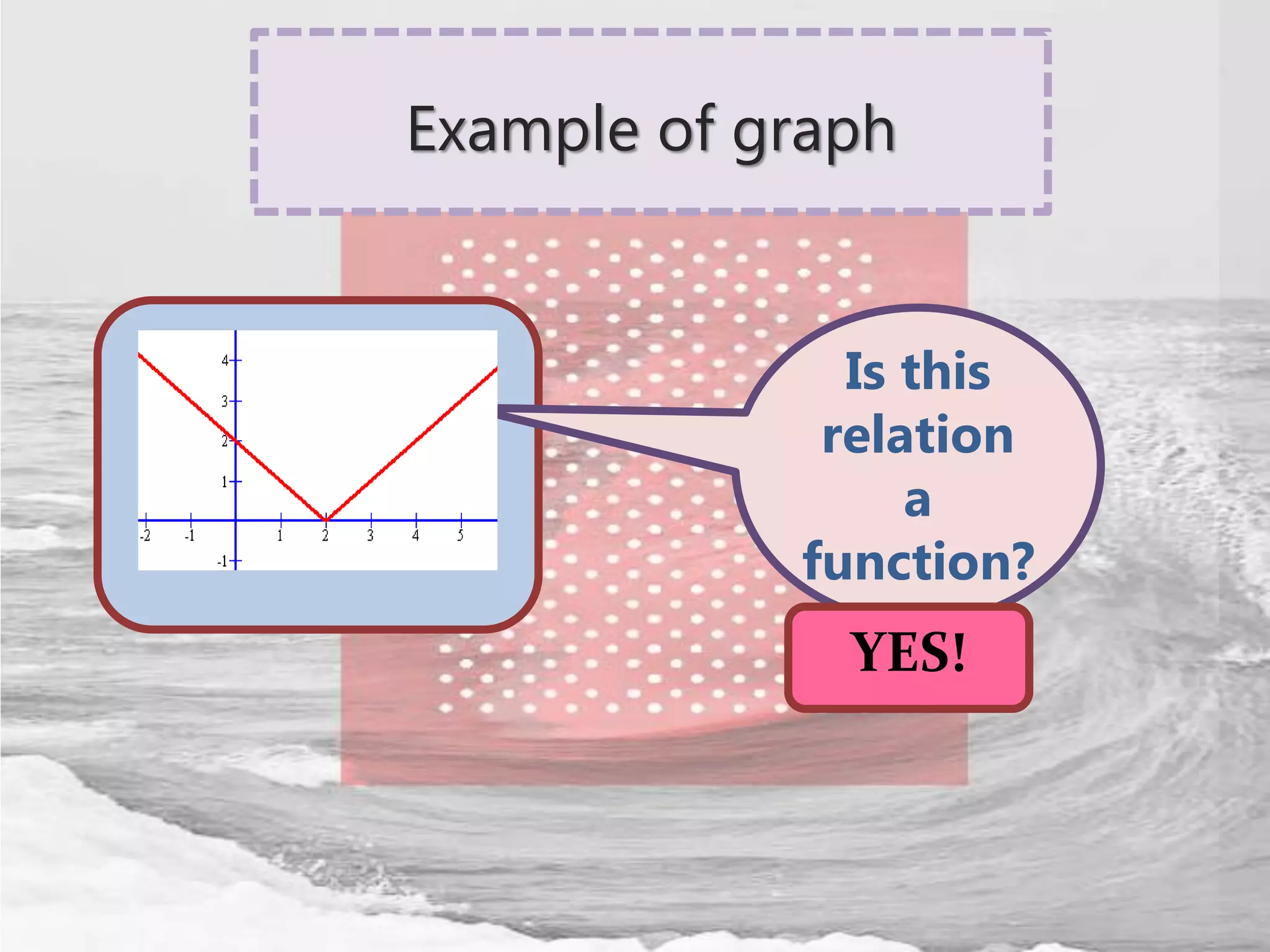
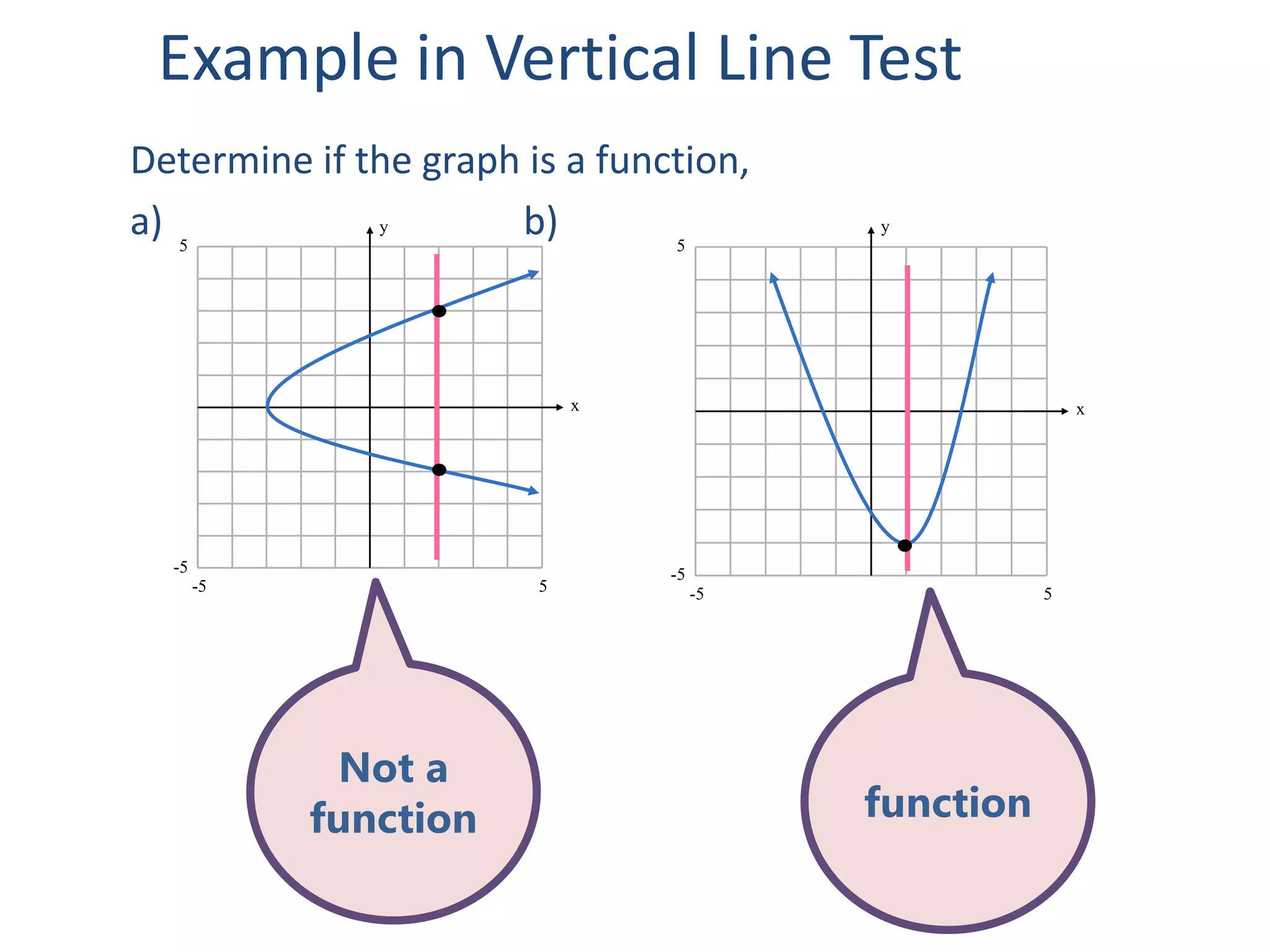
The document defines relations and functions. A relation is a set of ordered pairs where the domain is the set of first coordinates and the range is the set of second coordinates. A function is a special type of relation where each element in the domain corresponds to exactly one element in the range. Functions can be represented as tables of values, ordered pairs, mappings, graphs or equations. The vertical line test can be used to determine if a graph represents a function - if no vertical line intersects the graph at more than one point, it is a function. Examples are provided to illustrate these concepts.

1. -
Relations
and
Functions

2. Definition
- A set of ordered
pairs.
- The domain of a
relation is the set of
first coordinates.
- The range is the set
of second
coordinates.
Relation

3. Definition
x-values
are inputs,
domain,
independent
variable
y-values
are outputs,
range,
dependent
variable

4. Example of relation
{(0, -5) , (1, -4) , (2, -3), (3, -2) , (4, -1), (5, 0)}
{(1, 5),(4, -4),(6, -3)

5. Identifying domain and range
What are the domain?
{( , ),( , ),( , ),( , ),( , ),( , )}    0 5 1 4 2 3 3 2 4 1 5 0
What are the range?
(0, 1, 2, 3, 4, 5)
(-5, -4, -3, -2, -1, 0)

6. Definition
- a SPECIAL
RELATION in
which each element
of the domain
corresponds to
exactly one
element of the
range.
Function

7. Characteristics
of Functions
1. Each element
in domain X must
be matched with
exactly one
element in range
Y.

8. Characteristics
of Functions 2. Some elements
in Y may not be
matched with
any element in X.

9. Characteristics
of Functions
3. Two or more
elements in X
may be matched
with the same
element in Y.

10. A function can
be represented
in different
ways.
1. Table of
Values
2. Ordered Pairs
3. Mapping
4. Graph
5. An equation

11. Example of table of values
Is this
relation
a
function?
YES!
What
are the
domain?
(0,1,2,3)
What
are the
range?
(4,-1,7,6)
x y
0 4
1 -1
2 7
3 6

12. Example of ordered pairs
{(5,1), (7,2), (4,-9), (0,2)
Is this
relation
a
function?
YES!
What
are the
domain?
(5,7,4,0)
What
are the
range?
(1,2,-9,2)

13. Example of mapping
Is this
relation
a
function?
YES!
What
are the
domain?
(3,1,0)
What
are the
range?
(-1,2,3)
3
1
0
–1
2
3

14. Set A is the domain
1
2
3
4
5
Set B is the range
2
10
8
6
4
Must use all the x’s
Let’s look at another relation and decide if it is a function.
The x value can only be assigned to one y
This is a function ---it
meets our conditions

15. 1
2
3
4
5
2
10
8
6
4
Is the relation shown above a function?
NO Why not???
2 was assigned both 4
and 10

16. Set A is the domain
1
2
3
4
5
Set B is the range
2
10
8
6
4
This is not a function---
it doesn’t assign each
x with a y
Check this relation out to determine if it is a function.

17. Example of graph
Is this
relation
a
function?
YES!

18. -
Vertical
Line Test
in function

19. Definition
- A graph represents
a function if and
only if no vertical
line intersects the
graph in more than
one point. Vertical
Line Test

20. y
x
5
5
-5
-5
y
x
5
5
-5
-5
Example in Vertical Line Test
Determine if the graph is a function,
a) b)
Not a
function function