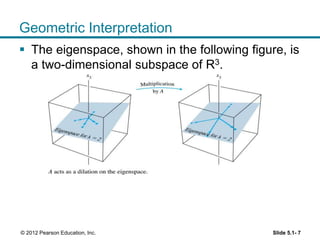
This document discusses eigenvalues and eigenvectors. It defines an eigenvector as a nonzero vector that does not change direction when a matrix is multiplied by it. An eigenvalue is a scalar value such that this equation is satisfied. The document provides examples of finding eigenvalues and eigenvectors. It also discusses eigenspaces, which are subspaces containing eigenvectors. Additionally, it covers the characteristic equation for finding eigenvalues of a matrix and discusses similarity of matrices.

1. 5
5.1
© 2012 Pearson Education, Inc.
Eigenvalues and Eigenvectors
EIGENVECTORS AND
EIGENVALUES

2. Slide 5.1- 2© 2012 Pearson Education, Inc.
EIGENVECTORS AND EIGENVALUES
Definition: An eigenvector of an nxn matrix A is a
nonzero vector x such that Ax=λx for some scalar
λ.
 A scalar λ is called an eigenvalue of A if there is a
nontrivial solution x of Ax=λx;
 such an x is called an eigenvector corresponding to λ.
 Eigenvectors may NOT be 0
 Eigenvalue may be 0

3. Eigenvectors - Example
Are u and v eigenvectors of A, for:
𝐴 =
1 6
5 2
, 𝐮 =
6
−5
, 𝑣 =
3
−2
Slide 5.1- 3© 2012 Pearson Education, Inc.

4. Finding Eigenvectors - Example
Show that 7 is an eigenvalue of A from
previous example and find corresponding
eigenvectors.
Slide 5.1- 4© 2012 Pearson Education, Inc.

5. Eigenspace
 General solution of Ax=λx is same as Nul
space of (A – λI)
 Subspace of Rn
 Called “Eigenspace”
 Contains 0 and all eigenvectors
Slide 5.1- 5© 2012 Pearson Education, Inc.

6. Finding Basis for Eigenspace - Example
A has eigenvalue of 2. Find basis for
corresponding eigenspace.
𝐴 =
4 −1 6
2 1 6
2 −1 8
Slide 5.1- 6© 2012 Pearson Education, Inc.

7. Slide 5.1- 7© 2012 Pearson Education, Inc.
Geometric Interpretation
 The eigenspace, shown in the following figure, is
a two-dimensional subspace of R3.

8. Slide 5.1- 8© 2012 Pearson Education, Inc.
EIGENVALUES of Triangular Matrix
 Theorem 1: The eigenvalues of a triangular
matrix are the entries on its main diagonal.
 Proof: For simplicity, consider the 3x3 case.
 If A is upper triangular, the (A – λI) has the form
11 12 13
22 23
33
11 12 13
22 23
33
λ 0 0
λ 0 0 λ 0
0 0 0 0 λ
λ
0 λ
0 0 λ
a a a
A I a a
a
a a a
a a
a
   
     
   
      
 
  
 
  

9. Slide 5.1- 9© 2012 Pearson Education, Inc.
EIGENVALUES of Triangular Matrix
 The scalar λ is an eigenvalue of A if and only if
the equation (A – λI) = 0 has a nontrivial
solution, i.e., iff the equation has a free variable.
 Because of the zero entries in (A – λI), it is easy
to see that (A – λI) = 0 has a free variable if and
only if at least one of the entries on the diagonal
of A – λI is zero.
 This happens if and only if λ equals one of the
entries a11, a22, a33 in A.

10. Slide 5.1- 10© 2012 Pearson Education, Inc.
EIGENVECTORS – Linear Independence
 Theorem 2: If v1, …, vr are eigenvectors that
correspond to distinct eigenvalues λ1, …, λr of an
nxn matrix A, then the set {v1, …, vr} is linearly
independent.

11. 0 as Eigenvalue
 If 0 is an eigenvalue:
 Ax=0x=0 has non-trivial solution
 A is NOT invertible
 Additions to IMT:
 (s) 0 is not an eigenvalue of A
 (t) |A| ≠ 0
Slide 5.1- 11© 2012 Pearson Education, Inc.

12. 5
5.1
© 2012 Pearson Education, Inc.
Eigenvalues and Eigenvectors
THE CHARACTERISTIC
EQUATION

13. Finding Eigenvalues - Example
Find the eigenvalues of 𝐴 =
2 3
3 −6
Slide 5.1- 13© 2012 Pearson Education, Inc.

14. Characteristic Equation
 characteristic equation: |A – λI| = 0
 Scalar equation
 Degree n, where A is nxn
 Solutions are eigenvalues of A
Slide 5.1- 14© 2012 Pearson Education, Inc.

15. Slide 5.2- 15© 2012 Pearson Education, Inc.
THE CHARACTERISTIC EQUATION
 Example 2: Find the characteristic equation of
5 2 6 1
0 3 8 0
0 0 5 4
0 0 0 1
A
  
 
 
 
 
 

16. Slide 5.2- 16© 2012 Pearson Education, Inc.
SIMILARITY
 If A and B are nxn matrices, then A is similar to
B if there is an invertible matrix P such that
 P-1AP = B, or, equivalently
 A = PBP-1
 Changing A into B is called a similarity
transformation.

17. Slide 5.2- 17© 2012 Pearson Education, Inc.
SIMILARITY
 Theorem 4: If nxn matrices A and B are similar,
then they have the same characteristic polynomial
and hence the same eigenvalues (with the same
multiplicities).