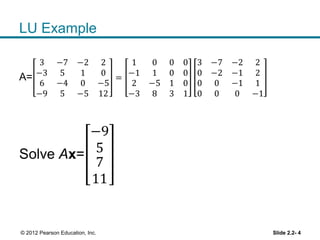
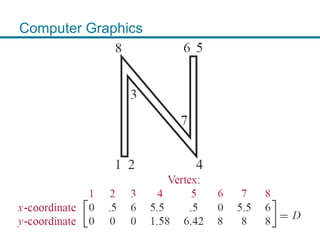
The document discusses LU factorization for solving systems of linear equations Ax = b. It explains that LU factorization factors a matrix A into lower and upper triangular matrices L and U, and that this can be used to solve systems of linear equations by first solving Ly = b for y, and then solving Ux = y for x. It also briefly discusses computer graphics topics like translations using homogeneous coordinates, and properties of determinants such as cofactor expansion and how row operations affect the determinant.

1. © 2012 Pearson Education, Inc.
Math 337-102
Lecture 6
LU Factorization
Computer Graphics
Determinants

2. Slide 2.2- 2© 2012 Pearson Education, Inc.
LU Factorization
 Factor A = LU
 A is mxn
 A does NOT have to be square!!!
 L is mxm (square) – Lower Triangular with 1’s on the
diagonal
 U is mxn  REF(A)

3. Using LU to Solve Ax = b
 Ax = b
 (LU)x = b
 L(Ux) = b
 Let y = Ux
 Solve Ly = b
 Then Ux = y
Slide 2.2- 3© 2012 Pearson Education, Inc.

4. LU Example
Slide 2.2- 4© 2012 Pearson Education, Inc.

5. Finding L and U
 U is Row Echelon Form of A using row
replacement only
 No interchanges or scaling!!!!
 L entries are such that the same
sequence of row operations that reduce A
to U will reduce L to I.
Slide 2.2- 5© 2012 Pearson Education, Inc.

6. Finding L and U - Example
Slide 2.2- 6© 2012 Pearson Education, Inc.

7. Using LU to solve Ax = b
 Factor A as LU
 Solve Ly = b for y
 Solve Ux = y for x
Slide 2.2- 7© 2012 Pearson Education, Inc.

8. Computer Graphics

9. Computer Graphics
Slide 2.2- 9© 2012 Pearson Education, Inc.

10. Translations – Homogeneous Coordinates
Slide 2.2- 10© 2012 Pearson Education, Inc.

11. Determinants
Slide 2.2- 11© 2012 Pearson Education, Inc.

12. Determinants – Co-Factors
Slide 2.2- 12© 2012 Pearson Education, Inc.

13. Determinants by Co-Factor Expansion
Slide 2.2- 13© 2012 Pearson Education, Inc.

14. Cofactor Expansion Example
Slide 2.2- 14© 2012 Pearson Education, Inc.

15. Cofactor Expansion Example
Slide 2.2- 15© 2012 Pearson Education, Inc.

16. Determinants of Triangular Matrices
Slide 2.2- 16© 2012 Pearson Education, Inc.

17. Row Operations and Determinants
 Thm 3-3: Let A be a square matrix.
a)If a multiple of one row is added to another
row to produce a matrix B, then |B| = |A|
b)If two rows are interchanged to produce B,
then |B| = -|A|
c)If one row of A is multiplied by k to produce
B, then |B| = k|A|
Slide 2.2- 17© 2012 Pearson Education, Inc.

18. Row Operations and Determinants
 Row replacement does not change determinant
 Row interchange negates the determinant
 Scaling – think of as factoring
Slide 2.2- 18© 2012 Pearson Education, Inc.