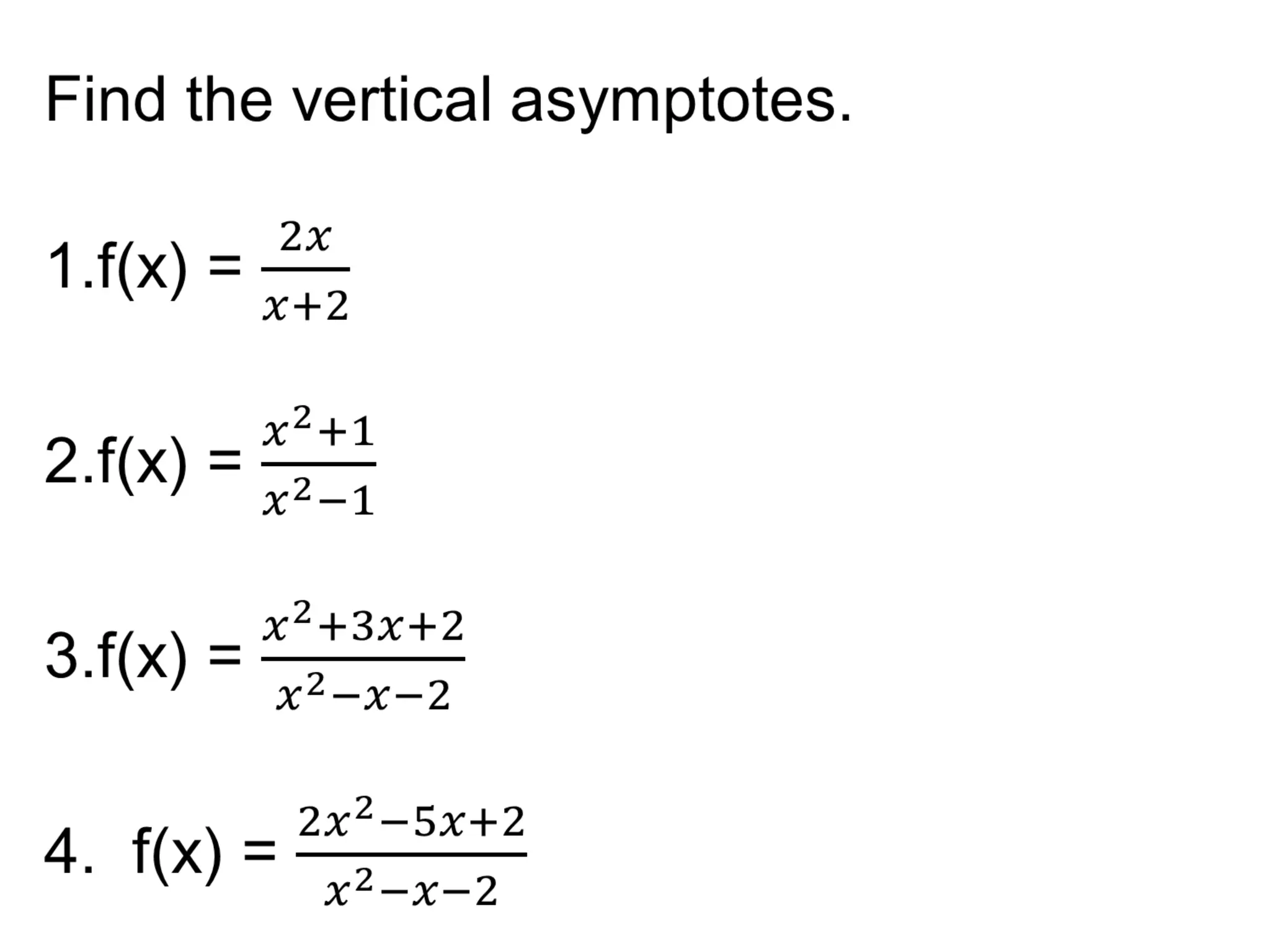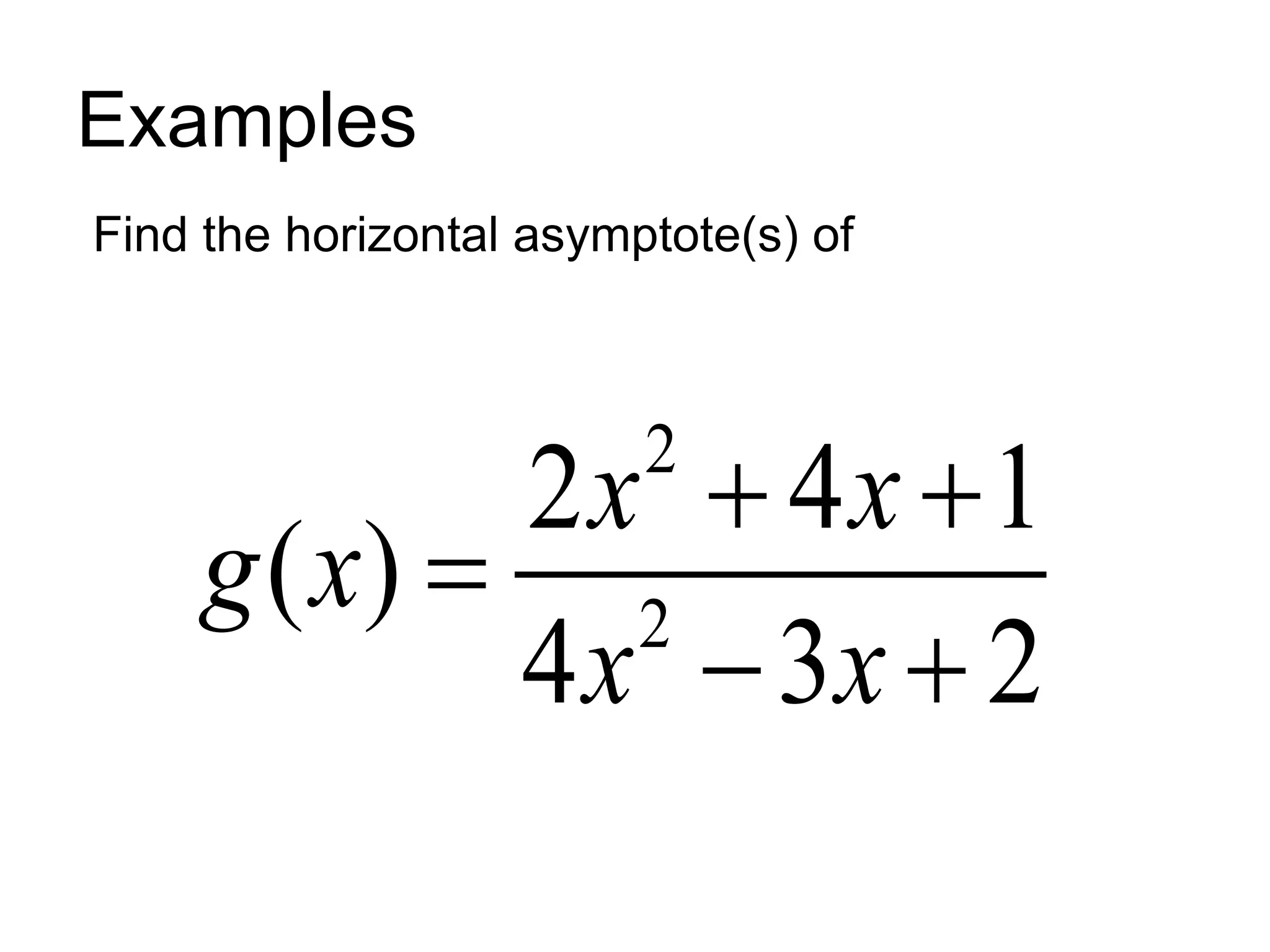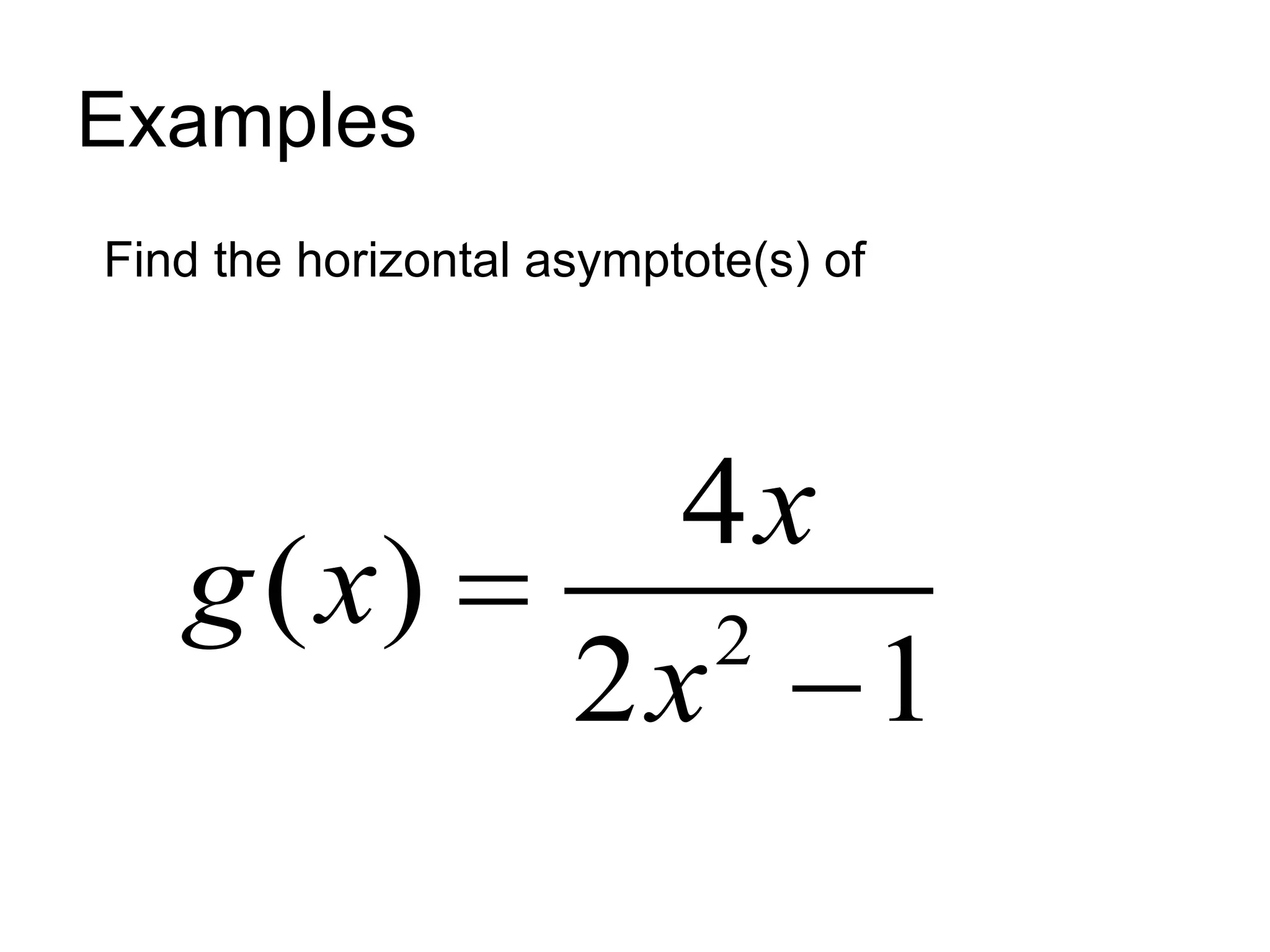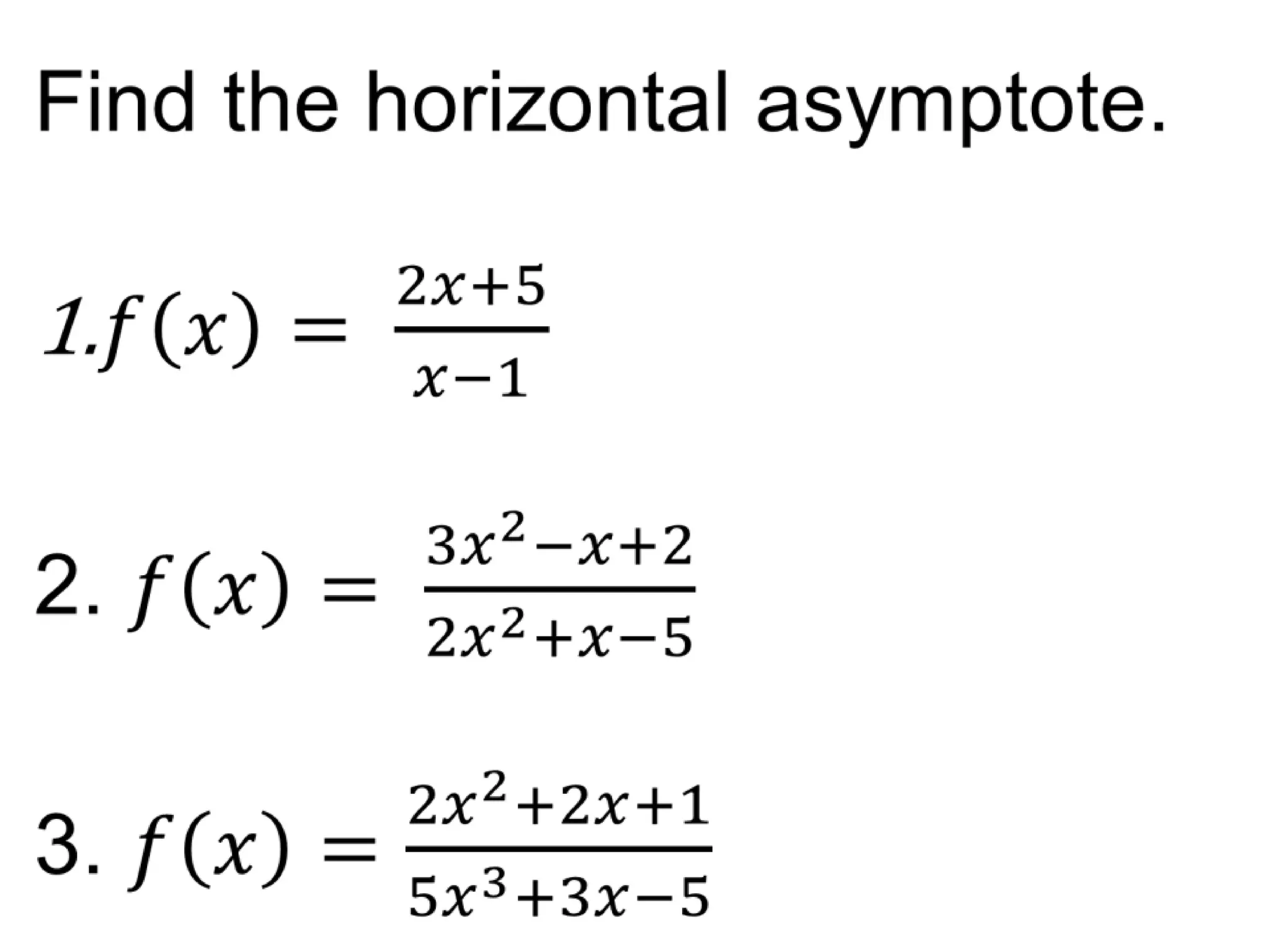This document discusses limits at infinity, asymptotes, and evaluating infinite limits. It defines an asymptote as a boundary line for a function's graph that the function approaches as the input value approaches positive or negative infinity. Vertical asymptotes occur when the denominator of a rational function equals 0, while horizontal asymptotes occur when the degree of the numerator is less than or equal to the degree of the denominator. Examples are provided for finding vertical and horizontal asymptotes. The document also provides a definition and theorem for evaluating limits at infinity.

1. More about
limits and
asymptotes

2. Objectives
1.Analyzing limits at infinity
2.Determining horizontal and vertical
asymptotes
3.Applying limits at infinity

5. Asymptotes

6. Definition of an asymptote
• An asymptote is a straight line which acts as a
boundary for the graph of a function.
• When a function has an asymptote (and not all
functions have them) the function gets closer
and closer to the asymptote as the input value to
the function approaches either a specific value a
or positive or negative infinity.
• The functions most likely to have asymptotes are
rational functions

7. Limits at Infinity

8. Limits at Infinity
•To help evaluate
limits at infinity,
use the following
definition.

9. Special Limits at infinity
Provided that x n is always defined.

11. Vertical Asymptotes
Vertical asymptotes occur when the
following condition is met:
The denominator of the simplified
rational function is equal to 0.

12. Finding Vertical Asymptotes
Example 1
 
x
x
x
f
2
2
5
2




13. Finding Vertical Asymptotes
Example 2
 
9
12
10
2
2
2




x
x
x
x
f

14. Finding Vertical Asymptotes
Example 3
 
6
5
2




x
x
x
x
g

16. Horizontal Asymptotes
Horizontal asymptotes occur when either one of the following
conditions is met:
The degree of the numerator is less than the degree of the
denominator. In this case the asymptote is the horizontal line
y = 0.
The degree of the numerator is equal to the degree of the
denominator. In this case the asymptote is the horizontal line
When the degree of the numerator is greater than the degree of
the denominator there is no horizontal asymptote

17. Examples
Find the horizontal asymptote(s) of
2
2
3
( )
1
x
f x
x



18. Examples
Find the horizontal asymptote(s) of
2
2
2 4 1
( )
4 3 2
x x
g x
x x
 

 

19. Examples
Find the horizontal asymptote(s) of
2
4
( )
2 1
x
g x
x



21. Infinite limits

22. Theorem on Infinite Limits