Embed presentation
Download as PDF, PPTX







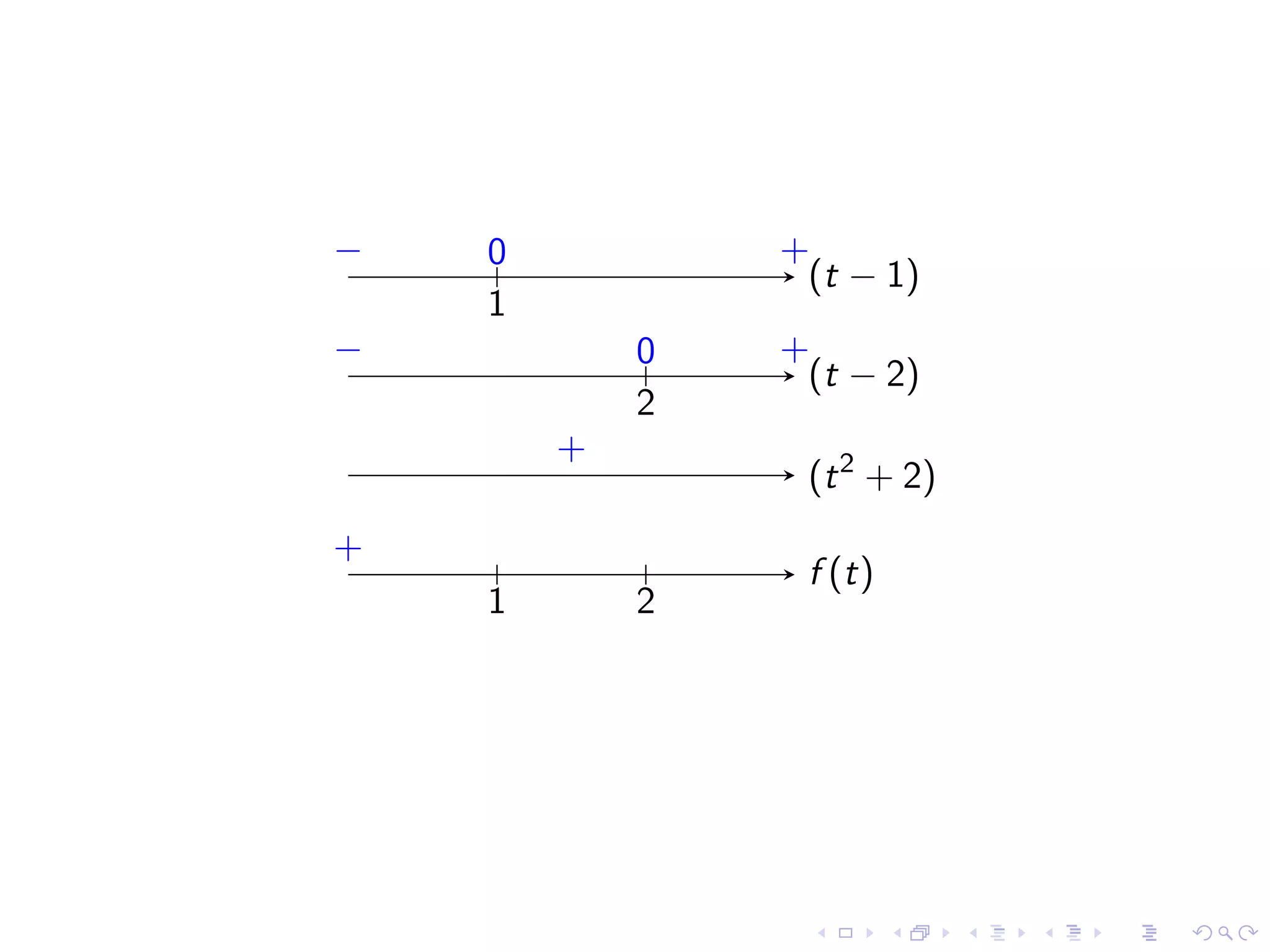
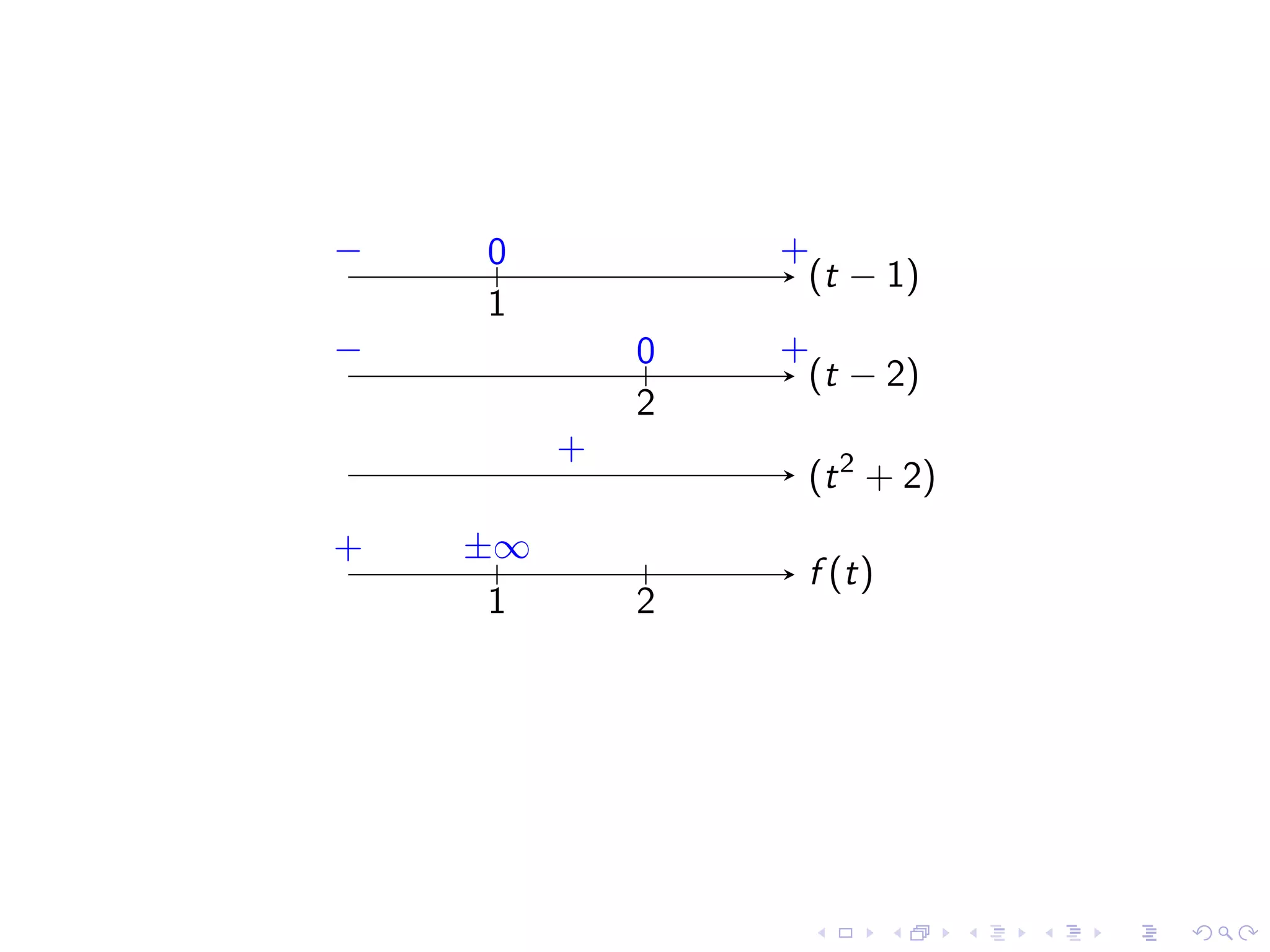

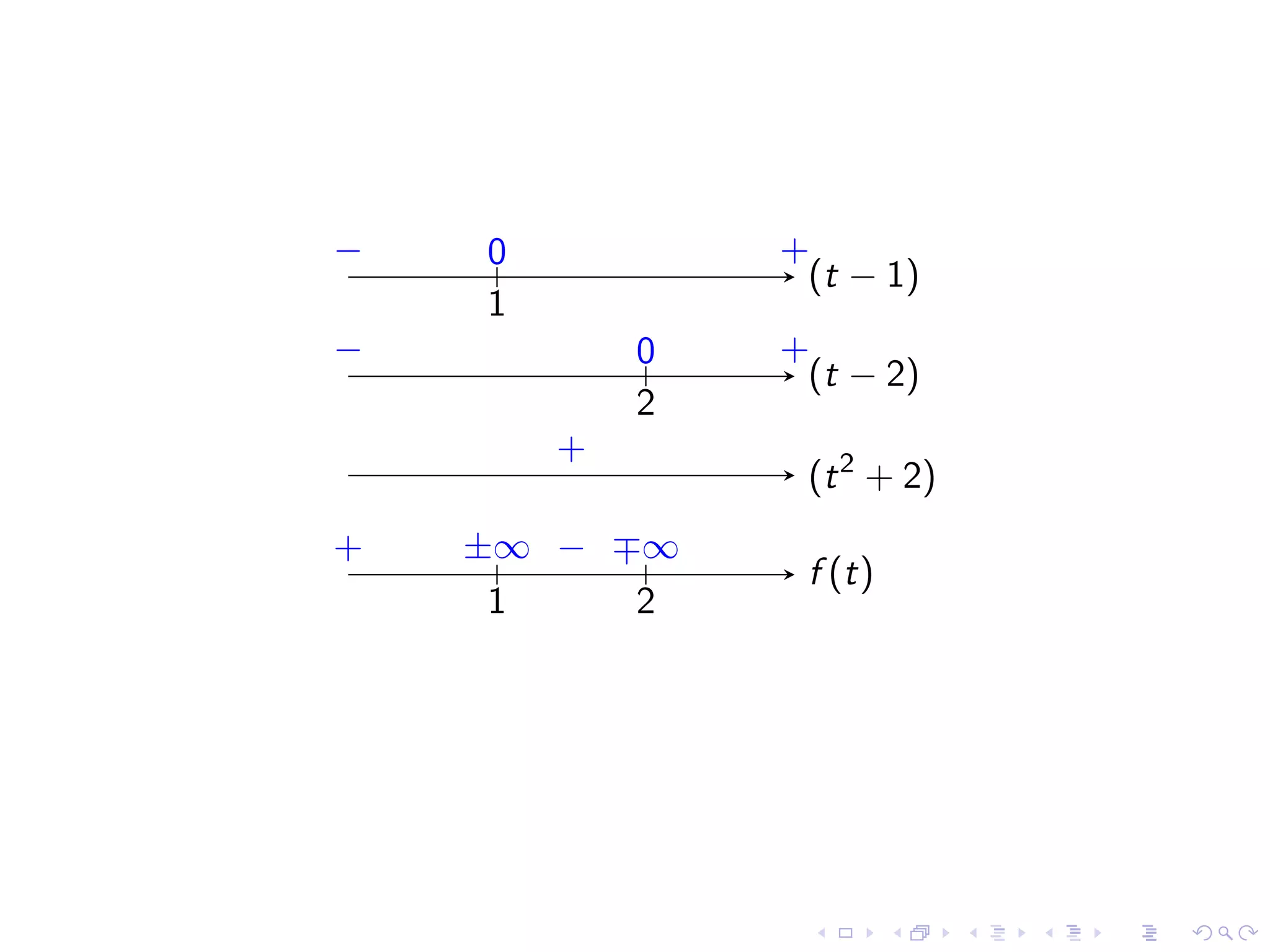
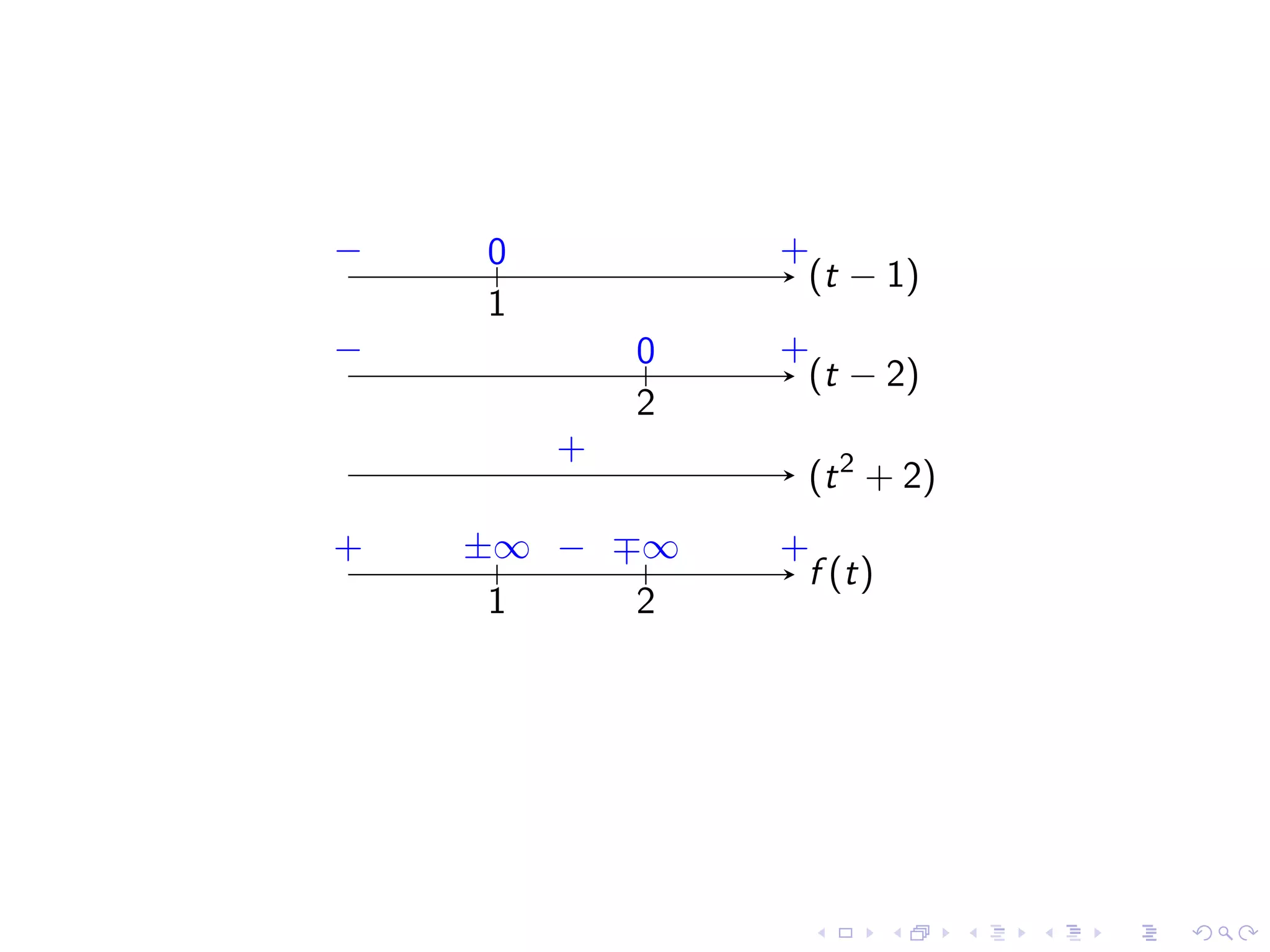























The document outlines concepts related to limits in calculus, focusing on infinite limits, vertical asymptotes, and the evaluation of limits at points of discontinuity. It provides definitions and rules for understanding and working with infinite limits, including examples and case studies. Additionally, it discusses indeterminate forms and offers techniques for factoring and rationalizing expressions to find limits.
Introduction to infinite limits, vertical asymptotes, and definitions for limits approaching infinity.
Exploring examples of infinite limits and identifying behaviors of functions at discontinuities.
Discussing limit laws involving infinite values, including sum, product, and quotient rules for limits.
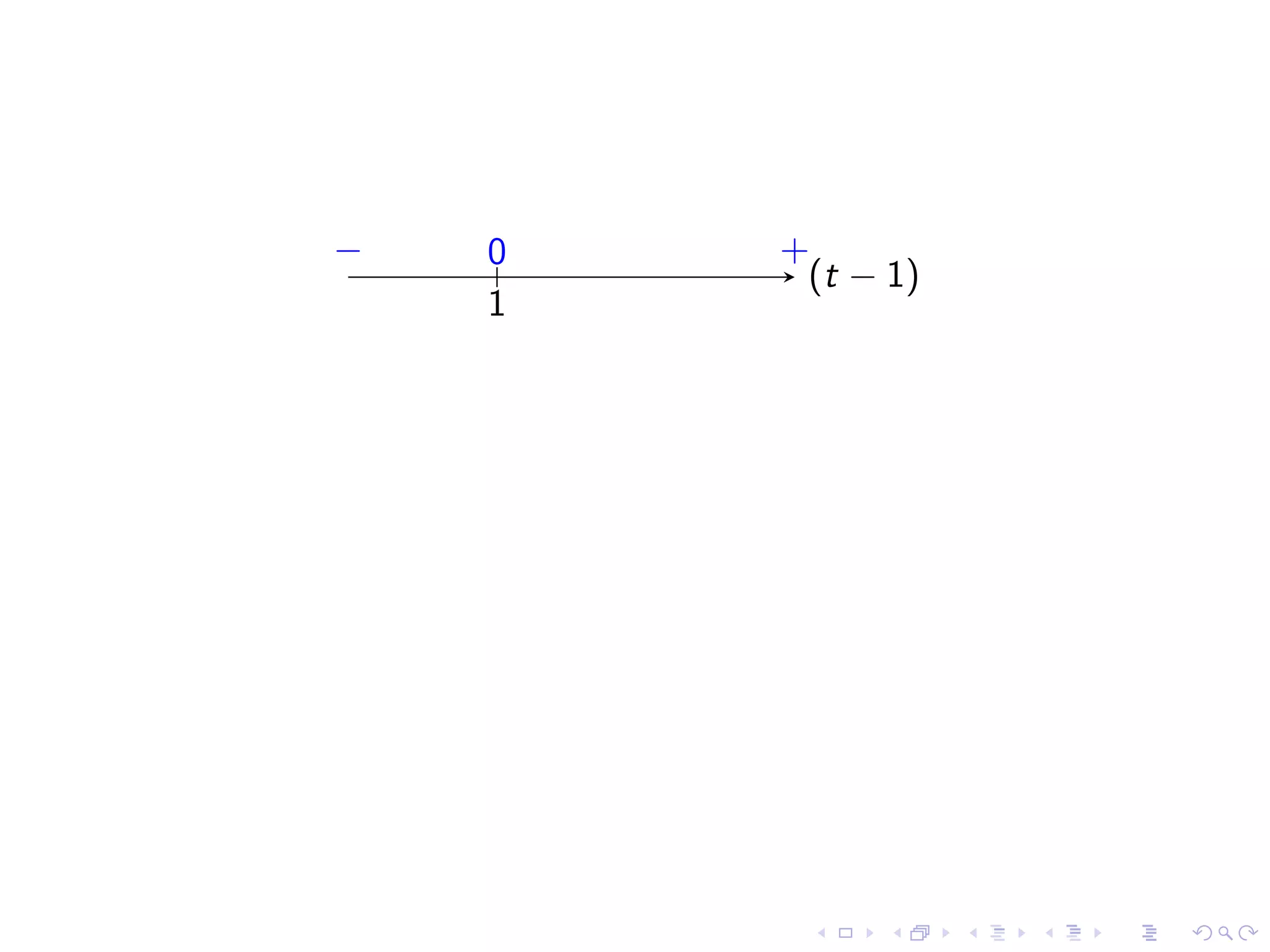
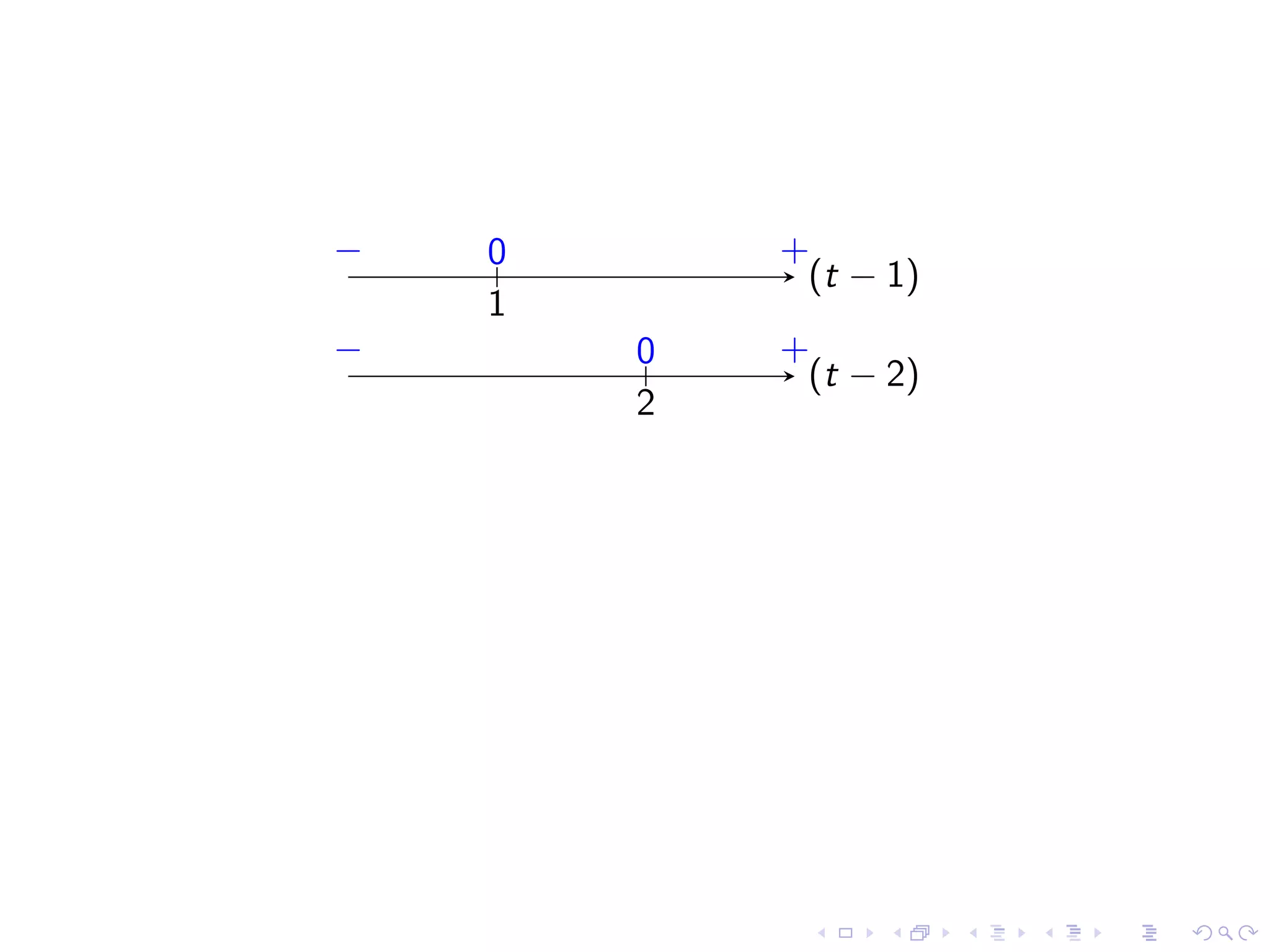
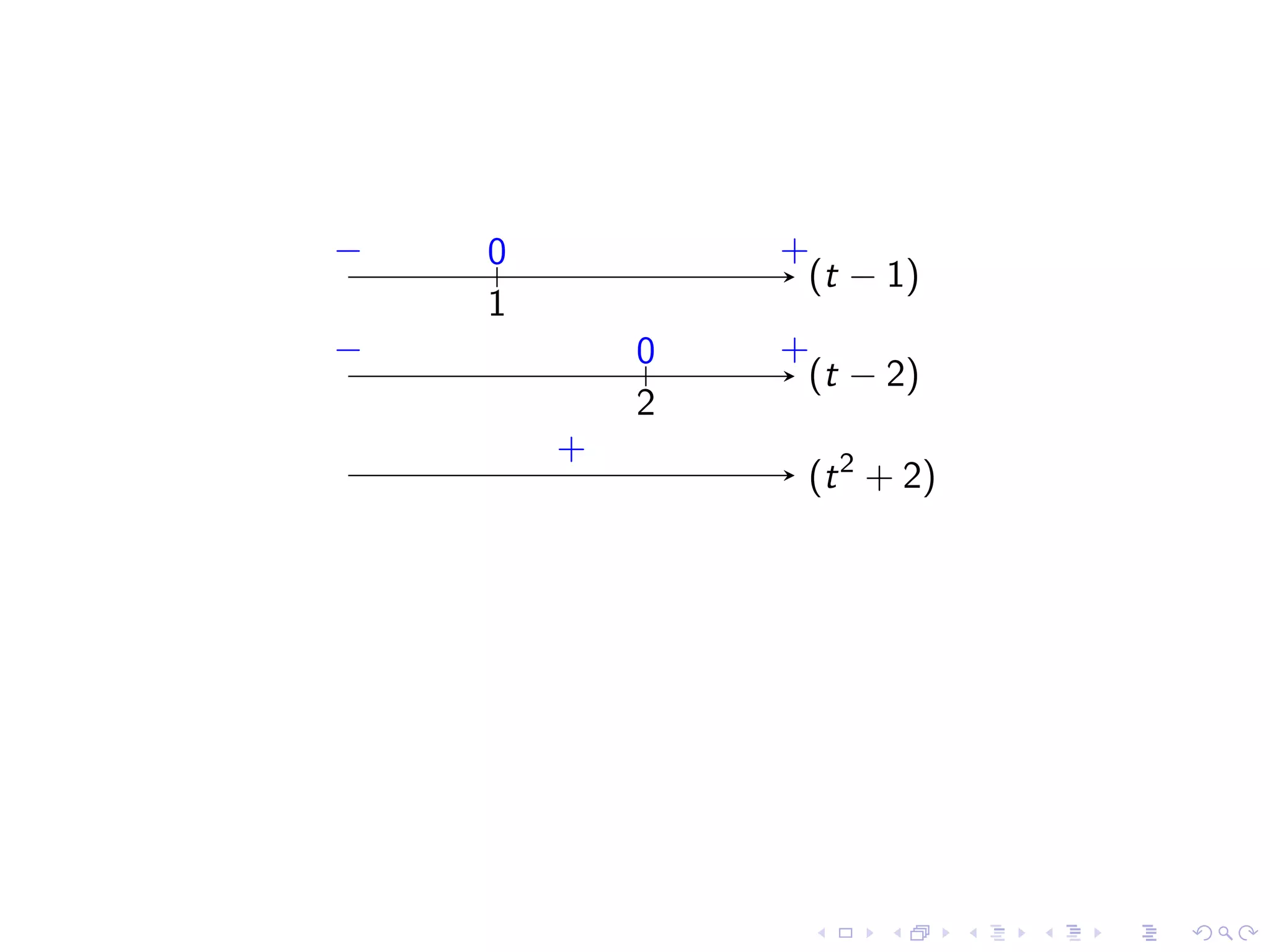
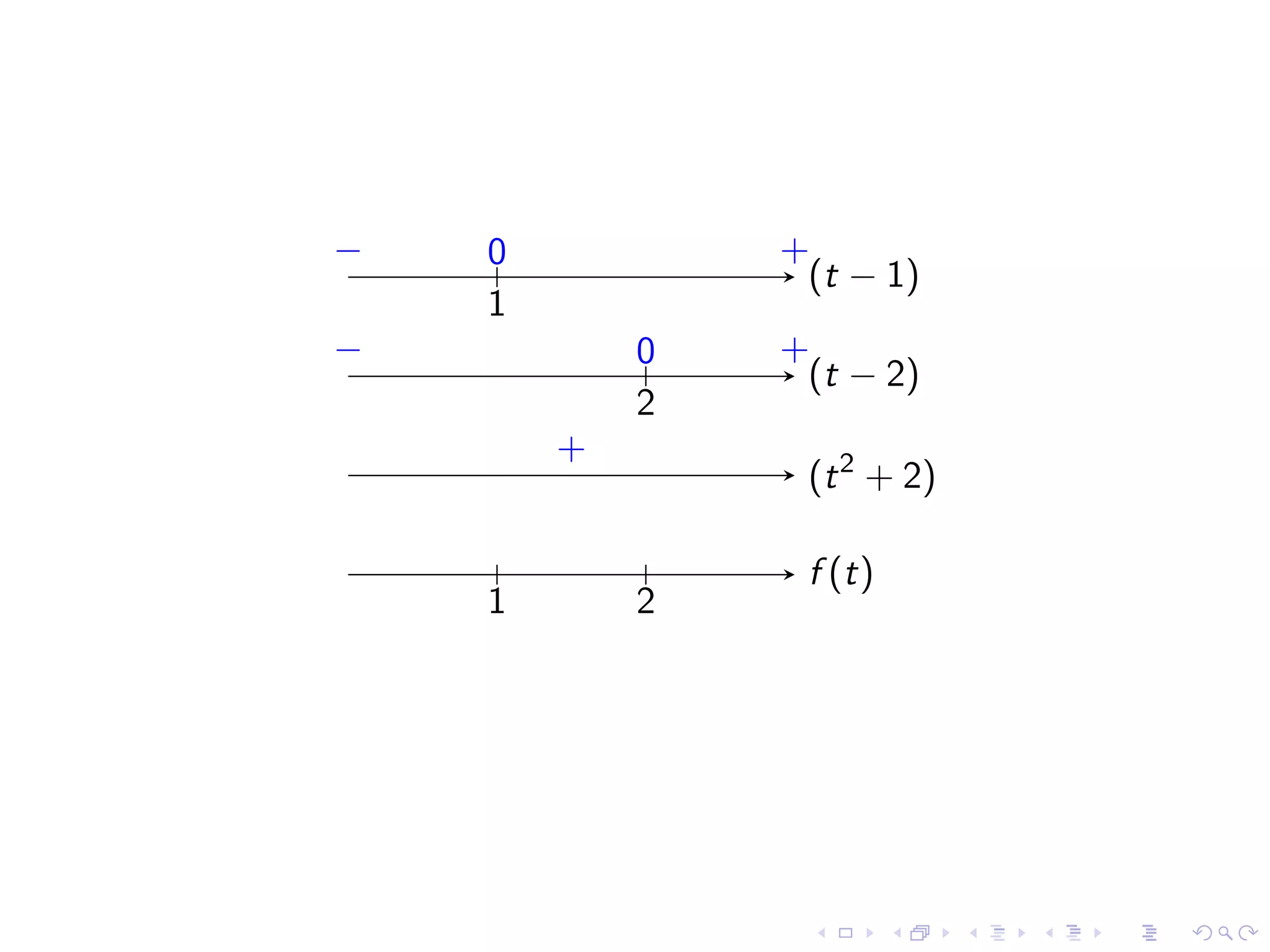
Identifying common indeterminate forms and the necessity to analyze them in detail for limit evaluation.
Definitions regarding limits at infinity, horizontal asymptotes, and how to find specific limits.
Worked examples computing limits at infinity by factoring polynomials and analyzing highest degree terms.
Comparative analysis of limits involving exponential growth and algebraic expressions as x approaches infinity.
Methods of rationalizing expressions to facilitate the calculation of limits that resemble indeterminate forms.
Overview of infinite limits, vertical asymptotes, and techniques introduced; reminder of worksheet.





































