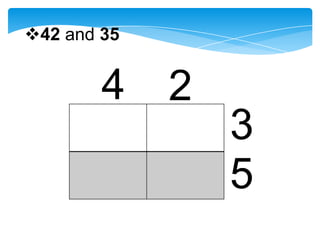
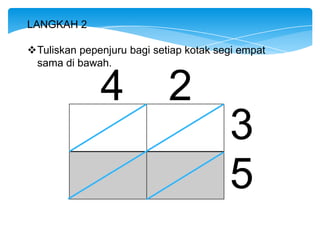
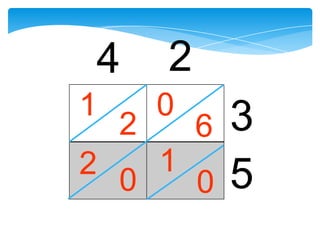
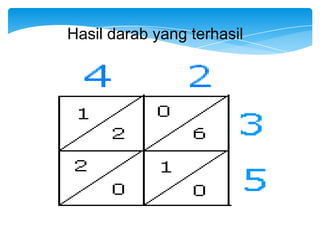
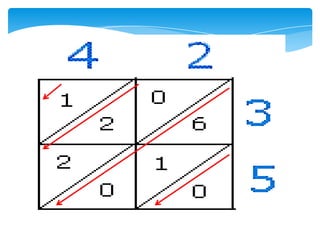
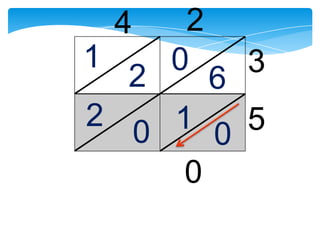
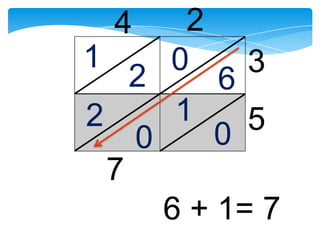
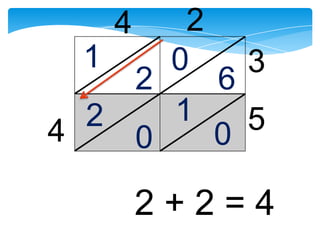
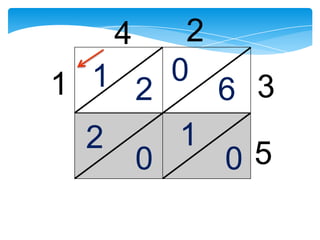
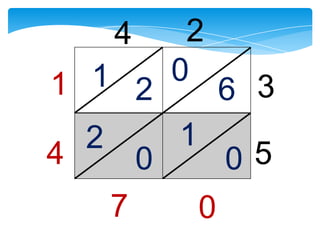
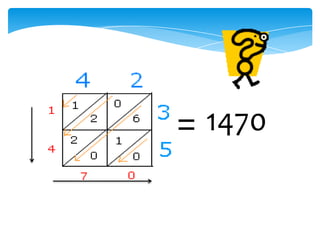
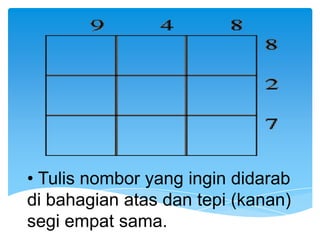
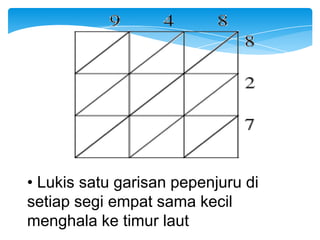
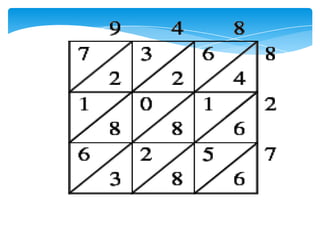
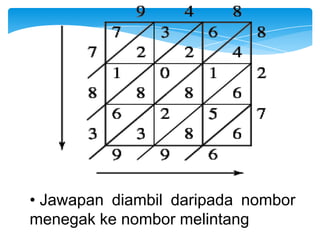
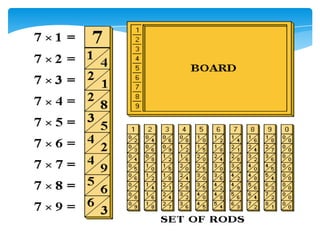
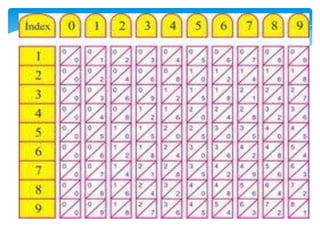
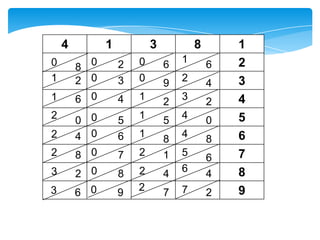
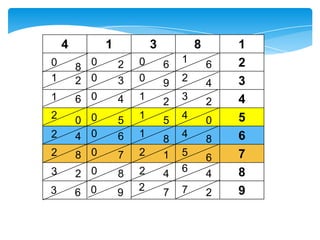
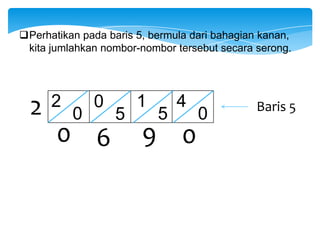
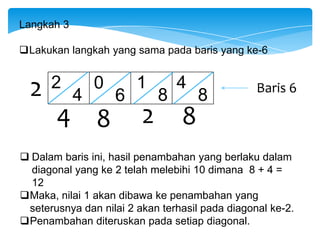
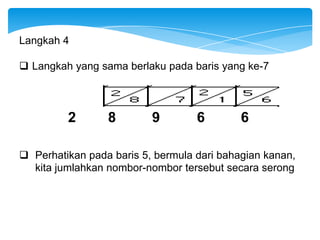
Dokumen ini membahas tentang kaedah pendaraban menggunakan metode lattice dan rod Napier. Metode ini dijelaskan dengan langkah-langkah mendarab dua bilangan dan cara menghitung hasilnya. Selain itu, dokumen juga membagikan contoh penerapan untuk kedua metode tersebut.

1. LATTICE METHOD AND
NAPIER’S ROD/
NAPIER’S BONES
DI S E DI A K A N OL E H:
1. N E L L Y E N G G A M
2.A Z N I E ANI EZ AH
A H MA D J A I S
3.F A R A H S Y A Z WA N I
I S MA I L
4.I R E N E B U N S I E A N A K

2. LATTICE
METHOD

3. Kaedah kekisi (lattice method) adalah
kaedah yang telah diperkenalkan dan
digunakan di Parsi dan India.
Ia adalah satu kaedah pendaraban yang
menggunakan kaedah lattice untuk
mendarab dua nombor.
Ia telah diterangkan oleh Al-Khwarizmi
pada abad ke-9, dan dibawa ke Eropah
oleh Fibonacci.

4. Types of order
2x2
2x3
3x2
3x3

5. CONTOH
2X2

6. CONTOH:
LANGKAH 1
Darabkan nilai 42 and 35
Susunkan masalah tersebut
dengan 1 nilai di bahagian atas
dan 1 lagi di bahagian tepi 2 x 2
grid.

7. 42 and 35
4 2
3
5

8. LANGKAH 2
Tuliskan pepenjuru bagi setiap kotak segi empat
sama di bawah.
4 2
3
5

9. Darabkan 4 dan 3 untuk mendapatkan
nilai 12 dan letakkannya pada
persilangan antara baris pertama dan
lajur pertama.
Carikan nilai yang selanjutnya dengan
mengulangi langkah yang sama.

10. 4 2
1 0 3
2 6
2 1
0 0 5

11. Hasil darab yang terhasil

12. LANGKAH 3
Tambahkan nilai-nilai yang
didapati di atas mengikut anak
panah bermula dari bahagian
kanan ke kiri grid tersebut.

14. 4 2
1 0 3
2 6
2 1 5
0 0
0

15. 4 2
1 0 3
2 6
2 1 5
0 0
7
6 + 1= 7

16. 4 2
1 0 3
2 6
2 1 5
4 0 0
2+2=4

17. 4 2
1 1 2 0
6 3
2 1
0 05

18. 4 2
1 1 2 0
6 3
2 1
4 0 05
7 0

19. Bagi mendapatkan jawapan bagi
42x35, kita perlu membaca hasil
darab yang berwarna merah secara
menurun dari bahagian kiri dan ke
bahagian kanan bawah.

20. = 1470

21. CONTOH
3X3

22. • Tulis nombor yang ingin didarab
di bahagian atas dan tepi (kanan)
segi empat sama.

23. • Lukis satu garisan pepenjuru di
setiap segi empat sama kecil
menghala ke timur laut

24. • Darabkan nombor di bahagian atas
ruang dan nombor di bahagian kanan.
• Bagi hasil darab yang mempunyai nilai
tempat puluh, nombor yang mempunyai
nilai tempat ‘puluh’ ditulis di bahagian atas
pepenjuru dan nombor yang mempunyai
nilai tempat ‘sa’ ditulis di bahagian bawah
pepenjuru.
• Jika hasil darab kurang daripada 10,
tulis 0 di bahagian atas pepenjuru.

26. • Jawapan diambil daripada nombor
menegak ke nombor melintang

27. Napier’s
rod

28. Seorang ahli matematik, Scotland bernama John
Napier (1550-1617 AD) menemui konsep
logaritma.
Beliau mencipta kalkulator yang mudah untuk
mendarabkan mana-mana dua nombor
Kalkulator yang mudah dikenali
sebagai tulang Napier, atau rod Napier kerana
ia boleh dibina daripada tulang, kertas dan lain-
lain
Untuk membuat Napier’s rod (bones), 10 jalur
kertas diperlukan dan setiap satu dibahagi
kepada 9 bahagian.

31. How The Rods Were Used
Contoh:
Darabkan 4138 dengan 567
Langkah 1
 Carikan hasil darab bagi 4138
dengan nombor-nombor 1-9
 Selesaikan jadual tersebut
seperti di bawah ini:

32. 4 1 3 8 1
0 1
0 8 0 2 6 6 2
1 2 0 3 0 9 2 4 3
1 6 0 4 1 2 3 2 4
2 0 0 5 1 5 4 0 5
2 4 0 6 1
8 4 8 6
2 8 0 7 2 1 5 6 7
3 2 0 8 2 4 6 4 8
3 6 0 9 2 7 7 2 9

33. Langkah 2
Untuk mendarabkan nilai 4138 dengan
567, kita perlu mengenalpasti terlebih
dahulu nilai-nilai yang terdapat dalam
baris 5,6 dan juga 7.

34. 4 1 3 8 1
0 1
0 8 0 2 6 6 2
1 2 0 3 0 9 2 4 3
1 6 0 4 1 2 3 2 4
2 0 0 5 1 5 4 0 5
2 4 0 6 1
8 4 8 6
2 8 0 7 2 1 5 6 7
3 2 0 8 2 4 6 4 8
3 6 0 9 2 7 7 2 9

35. Perhatikan pada baris 5, bermula dari bahagian kanan,
kita jumlahkan nombor-nombor tersebut secara serong.
2 2 0 1 4 Baris 5
0 5 5 0
0 6 9 0

36. Langkah 3
Lakukan langkah yang sama pada baris yang ke-6
2 2 0 1 4 Baris 6
4 6 8 8
4 8 2 8
 Dalam baris ini, hasil penambahan yang berlaku dalam
diagonal yang ke 2 telah melebihi 10 dimana 8 + 4 =
12
Maka, nilai 1 akan dibawa ke penambahan yang
seterusnya dan nilai 2 akan terhasil pada diagonal ke-2.
Penambahan diteruskan pada setiap diagonal.

37. Langkah 4
 Langkah yang sama berlaku pada baris yang ke-7
2 8 9 6 6
 Perhatikan pada baris 5, bermula dari bahagian kanan,
kita jumlahkan nombor-nombor tersebut secara serong

38. Langkah 5
Bagi mencari hasil darab nilai di atas, maka
hasil tambah bagi setiap diagonal yang
terdapat pada baris 5,6 dan 7 akan dijumlahkan
seperti yang berikut:
Baris
20690 5
24828 6
28966 7
2346246

39.  Oleh itu, didapati bahawa hasil
darab bagi 4138 dengan 567
adalah
= 2346246