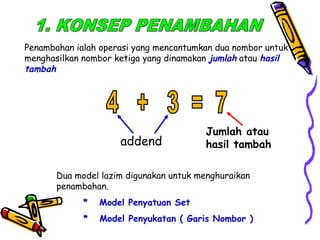
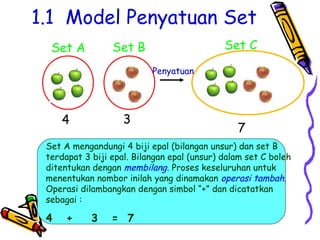
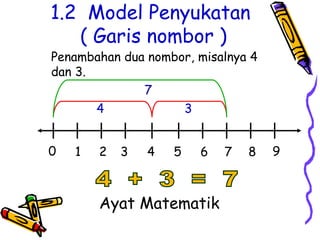
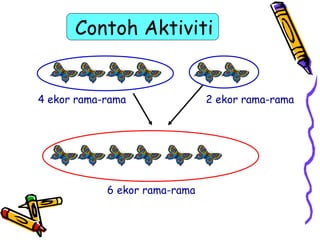
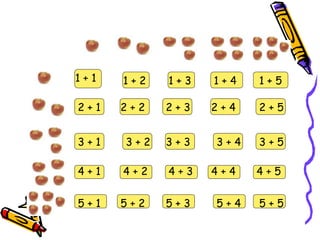
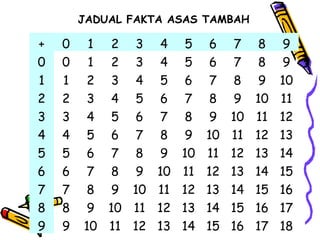
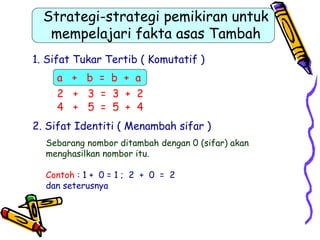
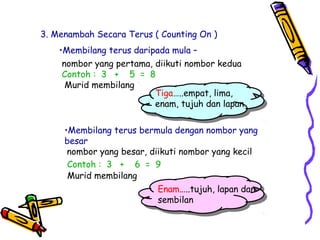
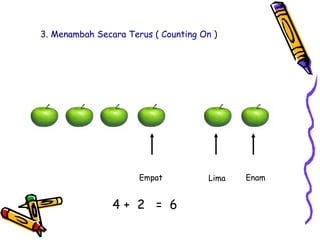
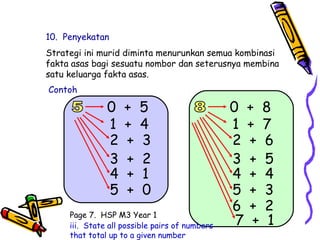
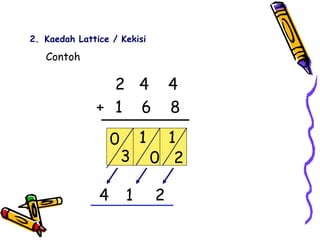
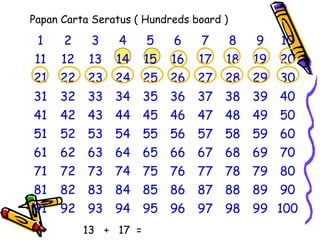
Dokumen tersebut membahas tentang pentingnya memahami konsep dasar matematika dan bagaimana aktivitas yang beragam dapat memudahkan proses pemahaman siswa untuk menerapkan ide-ide matematika ke situasi yang berbeda. Dokumen tersebut juga menjelaskan konsep penambahan dan berbagai strategi untuk memperkenalkan dan mempelajari konsep tersebut kepada siswa.

2. Penekanan kefahaman konsep dalamPenekanan kefahaman konsep dalam
matematik dan bagaimana aktivitimatematik dan bagaimana aktiviti
yang pelbagai bentuk dapatyang pelbagai bentuk dapat
mempermudahkan proses itu akanmempermudahkan proses itu akan
membantu pelajar untukmembantu pelajar untuk
mengaplikasikan idea-ideamengaplikasikan idea-idea
matematik spesifik kepada situasimatematik spesifik kepada situasi
yang pelbagai.yang pelbagai.

3. Kejayaan atau kegagalan diperingkat
awal menyelesaikan masalah
penambahan memainkan peranan
penting dalam menentukan sikap
pelajar terhadap matematik pada
tahun-tahun selanjutnya dalam alam
persekolahan

4. Sebelum murid mula diperkenalkan dengan operasi tambah,
mereka sepatutnya telah boleh:
* membilang hingga 10
* menyusun kumpulan benda-benda sehingga 10
* membaca dan menulis angka hingga 1-10
* memadankan angka daripada 1-10 dengan perkataan
nombor
* mengenal simbol “0” dan perkataan “sifar” dan
faham apa maknanya.
* memahami konsep keabadian nombor

5. Penambahan ialah operasi yang mencantumkan dua nombor untuk
menghasilkan nombor ketiga yang dinamakan jumlah atau hasil
tambah
addend
Jumlah atau
hasil tambah
Dua model lazim digunakan untuk menghuraikan
penambahan.
* Model Penyatuan Set
* Model Penyukatan ( Garis Nombor )

6. 1.1 Model Penyatuan Set
Set A Set B Set C
4 3
7
Penyatuan
Set A mengandungi 4 biji epal (bilangan unsur) dan set B
terdapat 3 biji epal. Bilangan epal (unsur) dalam set C boleh
ditentukan dengan membilang. Proses keseluruhan untuk
menentukan nombor inilah yang dinamakan operasi tambah.
Operasi dilambangkan dengan simbol “+” dan dicatatkan
sebagai :
4 + 3 = 7

7. 1.2 Model Penyukatan
( Garis nombor )
1 2 3 4 5 6 7 8 90
4 3
7
Ayat Matematik
Penambahan dua nombor, misalnya 4
dan 3.

8. Aktiviti Memperkenalkan
Konsep Penambahan
Aktiviti-aktiviti awalan untuk
memperkenalkan konsep harus diberi
melalui mencantum set (kumpulan)
objek. Pengalaman-pengalaman ini
akan membantu pelajar memahami
huraian lisan tentang operasi tambah
serta simbol dan istilah yang
digunakan untuk operasi ini.

9. Contoh Aktiviti
4 ekor rama-rama 2 ekor rama-rama
6 ekor rama-rama

10. Bimbing pelajar menghuraikan secara lisan situasi
penambahan (ayat matematik dlm perkataan )seperti
4 ekor rama-rama dan 2 ekor rama-rama jumlahnya 6
ekor rama-rama
4 ekor rama-rama ditambah 2 ekor rama-rama bersamaan
6 ekor rama-rama
Jumlah 4 ekor rama-rama dan 2 ekor rama-rama ialah 6
ekor rama-rama
Perkataan “ jumlahnya ”, “ ialah ”, dan “ bersamaan ”
boleh diringkaskan dengan mengunakan simbol “ = ”.
4 + 2 ialah 6
atau 4 + 2 sama dengan 6
atau 6 ialah 4 + 2
Perkataan “ dan ”, “ ditambah ”, dan “ jumlah ”
semuanya membawa pengertian tambah, dan
simbolnya “ + ”.

11. Fakta Asas Penambahan
Setelah murid-murid memahami konsep
penambahan dan dapat menulis ayat matematik
dengan betul, barulah kita perkenalkan fakta
asas tambah termasuk strategi-strategi
mempelajarinya agar fakta-fakta diingat
kembali dengan cepat dan tepat
Semua murid boleh menyatakan fakta asas
dengan cepat dan tepat sekiranya diajar dengan
cara yang wajar. Guru mesti menentukan
bahawa muridnya telah mempunyai konsep
tambah termasuk simbol-simbol yang mantap
sebelum menyuruh murid menghafal. (peringkat
paling tinggi serta paling cekap bagi seseorang
pelajar)

13. 1 + 1 1 + 2 1 + 3 1 + 4 1 + 5
2 + 1 2 + 2 2 + 3 2 + 4 2 + 5
3 + 1 3 + 2 3 + 3 3 + 4 3 + 5
4 + 1 4 + 2 4 + 3 4 + 4 4 + 5
5 + 1 5 + 2 5 + 3 5 + 4 5 + 5

14. + 0 1 2 3 4 5 6 7 8 9
0 0 1 2 3 4 5 6 7 8 9
1 1 2 3 4 5 6 7 8 9 10
2 2 3 4 5 6 7 8 9 10 11
3 3 4 5 6 7 8 9 10 11 12
4 4 5 6 7 8 9 10 11 12 13
5 5 6 7 8 9 10 11 12 13 14
6 6 7 8 9 10 11 12 13 14 15
7 7 8 9 10 11 12 13 14 15 16
8 8 9 10 11 12 13 14 15 16 17
9 9 10 11 12 13 14 15 16 17 18
JADUAL FAKTA ASAS TAMBAH

15. Daripada 100 fakta asas penambahan yang diajar
kepada pelajar, didapat 16 kombinasi dianggap sukar
untuk diingat oleh pelajar.
9 + 8 atau 8 + 9
9 + 7 atau 7 + 9
9 + 6 atau 6 + 9
9 + 5 atau 5 + 9
8 + 7 atau 7 + 8
8 + 6 atau 6 + 8
9 + 4 atau 4 + 9
8 + 5 atau 5 + 8

16. Strategi-strategi pemikiran untuk
mempelajari fakta asas Tambah
1. Sifat Tukar Tertib ( Komutatif )
a + b = b + a
2 + 3 = 3 + 2
4 + 5 = 5 + 4
2. Sifat Identiti ( Menambah sifar )
Sebarang nombor ditambah dengan 0 (sifar) akan
menghasilkan nombor itu.
Contoh : 1 + 0 = 1 ; 2 + 0 = 2
dan seterusnya

17. 3. Menambah Secara Terus ( Counting On )
•Membilang terus daripada mula –
Murid membilang
Tiga…..empat, lima,
enam, tujuh dan lapan
•Membilang terus bermula dengan nombor yang
besar
nombor yang pertama, diikuti nombor kedua
Contoh : 3 + 5 = 8
nombor yang besar, diikuti nombor yang kecil
Murid membilang
Contoh : 3 + 6 = 9
Enam…..tujuh, lapan dan
sembilan

18. 3. Menambah Secara Terus ( Counting On )
Empat Lima Enam
4 + 2 = 6

19. 4. Menambah Satu
Menambah 1 kepada sebarang nombor akan memberi
nombor membilang yang seterusnya, seperti
5 + 1 = 6, 9 + 1 = 10
5. Kombinasi kepada 10
Murid menggunakan jari untuk mencari jumlah
(kombinasi 10 ), seperti
5 + 5 = 10, 6 + 4 = 10, 7 + 3 = 10 dan
seterusnya
6. Gandaan ( Doubles )
Gandaan seperti 1 + 1, 2 + 2, 3 + 3 dan seterusnya

20. 7. Hampir Gandaan atau Gandaan +1 dan +2
(“ Near Doubles ” atau “ Doubles +1 dan +2 ” )
Contoh 1 : 7 + 8
Gandaan yang hampir ialah 7 + 7.
Jika 7 + 7 = 14, maka 7 + 8 = 15
Atau, 7 + 8 = 7 + 7 + 1 = 15
Strategi gandaan
tambah satu (+1)
Contoh 2 :
8 + 7 = 8 + 8 – 1 = 15
Strategi gandaan
tolak satu (-1)
Contoh 3 :
5 + 7 = 5 + 5 + 2 = 10 + 2 = 12
Strategi gandaan
tambah dua (+2)
Contoh 4 :
7 + 5 = 7 + 7 – 2 = 14 – 2 = 12
Strategi gandaan
tolak dua (-2)

21. 8. Sifat Sekutuan / Menjadikan 10 / Penitian (bridging)
Jumlah untuk 9 + 5 boleh difikirkan 10 + 4 = 14 kerana:
Lain-lain contoh
8 + 7 = 8 + ( 2 + 5 )
= ( 8 + 2 ) + 5
= 10 + 5
= 15
9 + 8 = 9 + ( 1 + 7 )
= (9 + 1 ) + 7
= 10 + 7
= 17
9 + 5 = 9 + (1 + 4)
= (9 + 1 ) + 4
= 10 + 4
= 14
Sifat kalis sekutuan : n + (m + r) = (n + m) + r

22. 9. Tambah 9
Nombor 9 ditambah dengan sebarang nombor yang lain
adalah sama dengan 10 tambah nombor yang dikurang satu.
Contoh
9 + 4 = 10 + 3 = 13
9 + 6 = 10 + 5 = 15
9 + 3 = 10 + 2 = 12

23. 10. Penyekatan
Strategi ini murid diminta menurunkan semua kombinasi
fakta asas bagi sesuatu nombor dan seterusnya membina
satu keluarga fakta asas.
Contoh
0 + 5
1 + 4
2 + 3
3 + 2
4 + 1
5 + 0
0 + 8
1 + 7
2 + 6
3 + 5
5 + 3
4 + 4
6 + 2
7 + 1
Page 7. HSP M3 Year 1
iii. State all possible pairs of numbers
that total up to a given number

24. Algoritma Penambahan
Algoritma – bermakna prosedur atau
langkah-langkah serta format yang
digunakan untuk menyelesaikan
sesuatu masalah.

25. Sebelum algoritma lazim (conventional algorithm) yang biasa
digunakan, pelajar boleh diperkenalkan kepada algoritma
perkembangan ( development algorithm )
Bentuk Panjang (Perkataan )
25 = 2 puluh 5 sa
+ 56 = 5 puluh 6 sa
7 puluh 11 sa = 8 puluh 1 sa
Bentuk Panjang ( Angka )
25 = 20 + 5
+ 56 = 50 + 6
70 + 11 = 70 + (10 + 1 )
= (70 + 10) + 1
= 80 + 1
= 81
Jumlah Separa
25
+ 56
11
+ 70
81
Pu Sa
2 5
5 6+
1 1
7 0
8 1
Algoritma
lazim
25
+ 56
81
1

26. Kaedah- kaedah
Penambahan Lain
1. Kaedah Hasil Tambah Separa ( Method of Partial Sum )
34
+ 58
12
+ 80
92
Hasil tambah separa
(4 + 8)
(30 + 50)
Contoh
225
243
1 23
500
80
1 1
591
( 200 + 200 + 100 )
( 20 + 40 + 20 )
( 5 + 3 + 3 )
Perhatikan bahawa
penambahan boleh dibuat dari
kiri ke kanan juga

27. 2. Kaedah Lattice / Kekisi
Contoh
2 4 4
1 6 8
1
2
1
0
0
3
214
+

28. Cuba fikirkan
Bagaimana kita boleh menggunakan
alat ini untuk membantu pelajar
melakukan penambahan dekad tinggi
3 + 8 =
13 + 17 =
23 + 15 =

29. 1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
Papan Carta Seratus ( Hundreds board )
13 + 17 =