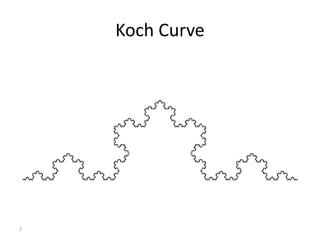
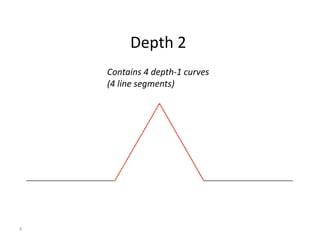
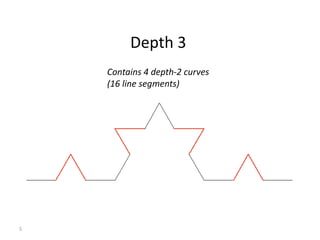
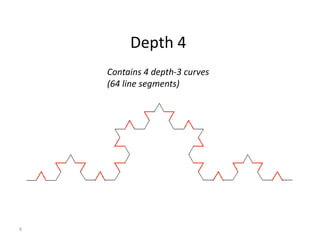
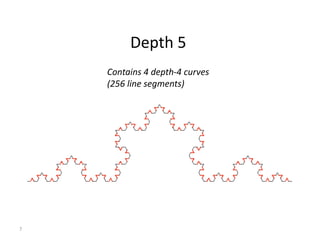
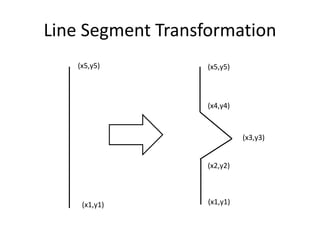
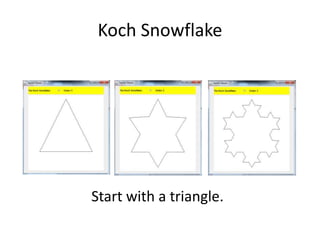
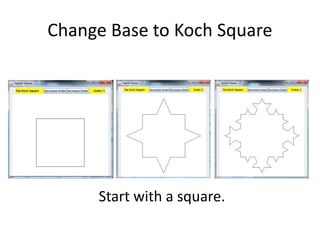
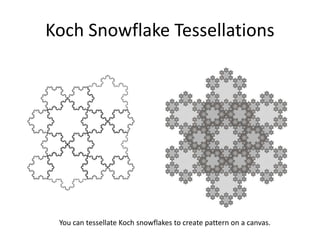
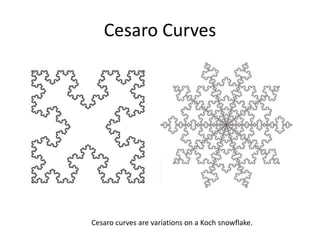
The document explains the Koch curve and related fractal concepts through a detailed algorithm and geometric transformations. It describes the iterative process of creating Koch curves and snowflakes, variations such as Cesaro curves, and how different shapes and ratios can affect the projections. It also addresses methods to emulate natural landmass shapes using randomness in the curve generation.

1. Koch Curves
The Walker School
APCSA
1

2. 2
Koch Curve

3. 3
Depth 1
1 line segment

4. 4
Depth 2
Contains 4 depth-1 curves
(4 line segments)

5. 5
Depth 3
Contains 4 depth-2 curves
(16 line segments)

6. 6
Depth 4
Contains 4 depth-3 curves
(64 line segments)

7. 7
Depth 5
Contains 4 depth-4 curves
(256 line segments)

8. 8
Pseudocode Algorithm
To make a Koch Curve:
• Draw a straight line if depth is zero; otherwise
draw four smaller Koch Curves.

9. Koch Curve
Start with a line.

10. Line Segment Transformation
(x1,y1)
(x2,y2)
(x3,y3)
(x4,y4)
(x5,y5)
(x1,y1)
(x5,y5)

11. Segment Calculations

12. Calculating the Projection
l
l
x = ½l
y = √3/2l
m2 + (½ l)2 = l2
m2 + ¼ l2 = l2
√m2 = √¾ l2
m = √3/2l * 1/3 = √3l/6
1/3 length of each iteration

13. Other Geometric Shapes?

14. Koch Snowflake
Start with a triangle.

15. Triangles Need 3 Calls to drawFractal()
Call the method drawFractal() for each side of the triangle. You need to
establish variables for the x,y coordinates for the line on each side of the base
triangle.

16. What aspects can you change?

17. Aspects
• Ratio Expression
• Shape of the Triangle
• Shape of the Base
– Square, Pentagon, Trapazoid
• Tessellations
• Color

18. Ratio Change to Projection
How does the projection change when you
change the ratio?

19. Change Ratio through Expressions

20. Change Base to Koch Square
Start with a square.

21. Calculates the Tip of the Projection
How does the projection change when you
change the ratio?

22. Square Needs 4 Calls to drawFractal()

23. How do we get curves that look
like landmasses?

24. 24
Fractals in Nature
Coastlines

25. 25
Fractals in Nature
Coastlines

26. 26
Fractals in Nature
Coastlines

27. 27
Fractals in Nature
Coastlines

28. 28
Fractals in Nature
Coastlines

29. 29
Fractals in Nature
Coastlines

30. 30
Fractals in Nature
Coastlines

31. Use the Random Class

32. Add Randomness to the Ration
Generates a random number
between 3 and 10 for the
denominator of the ratio.

33. 3 Calls to the Method drawFractal()

34. 6 Recursive Calls
Approximates Landmass

35. Examples for Inspiration

36. Koch Snowflake Tessellations
You can tessellate Koch snowflakes to create pattern on a canvas.

37. Cesaro Curves
Cesaro curves are variations on a Koch snowflake.

38. Koch Curve
(4/3n or log 4/log 3 = approx. 1.26)
https://www.behance.net/gallery/720515/Worlds-Largest-Fractal-Vectors

39. Contact
If you want the Java code for some of the basic
Koch Curves you can contact me at:
Thomas Cooper
The Walker School
Marietta, GA 30062
Website: http://www.thewalkerschool.org
Email: thomas.cooper@thewalkerschool.org