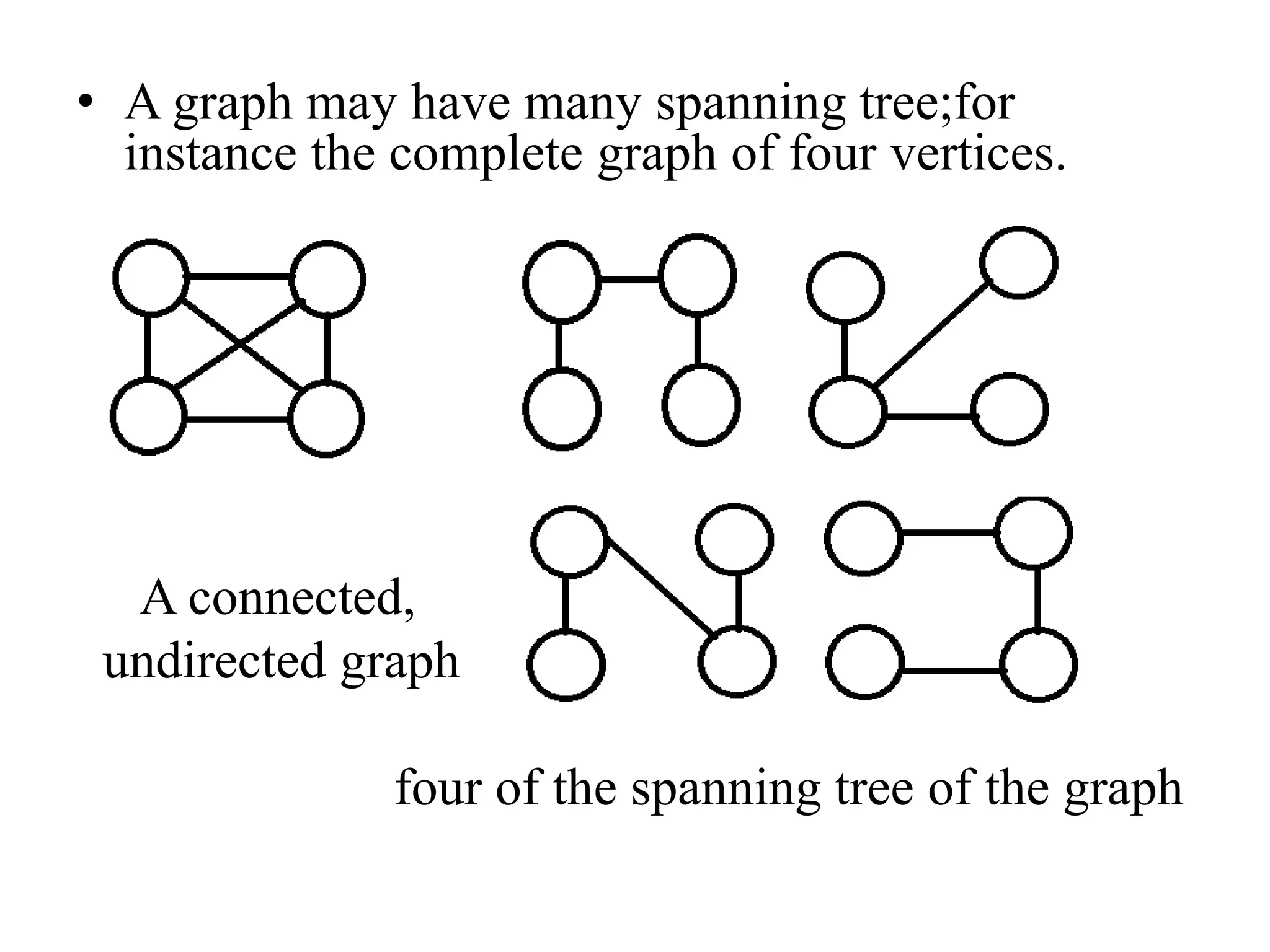
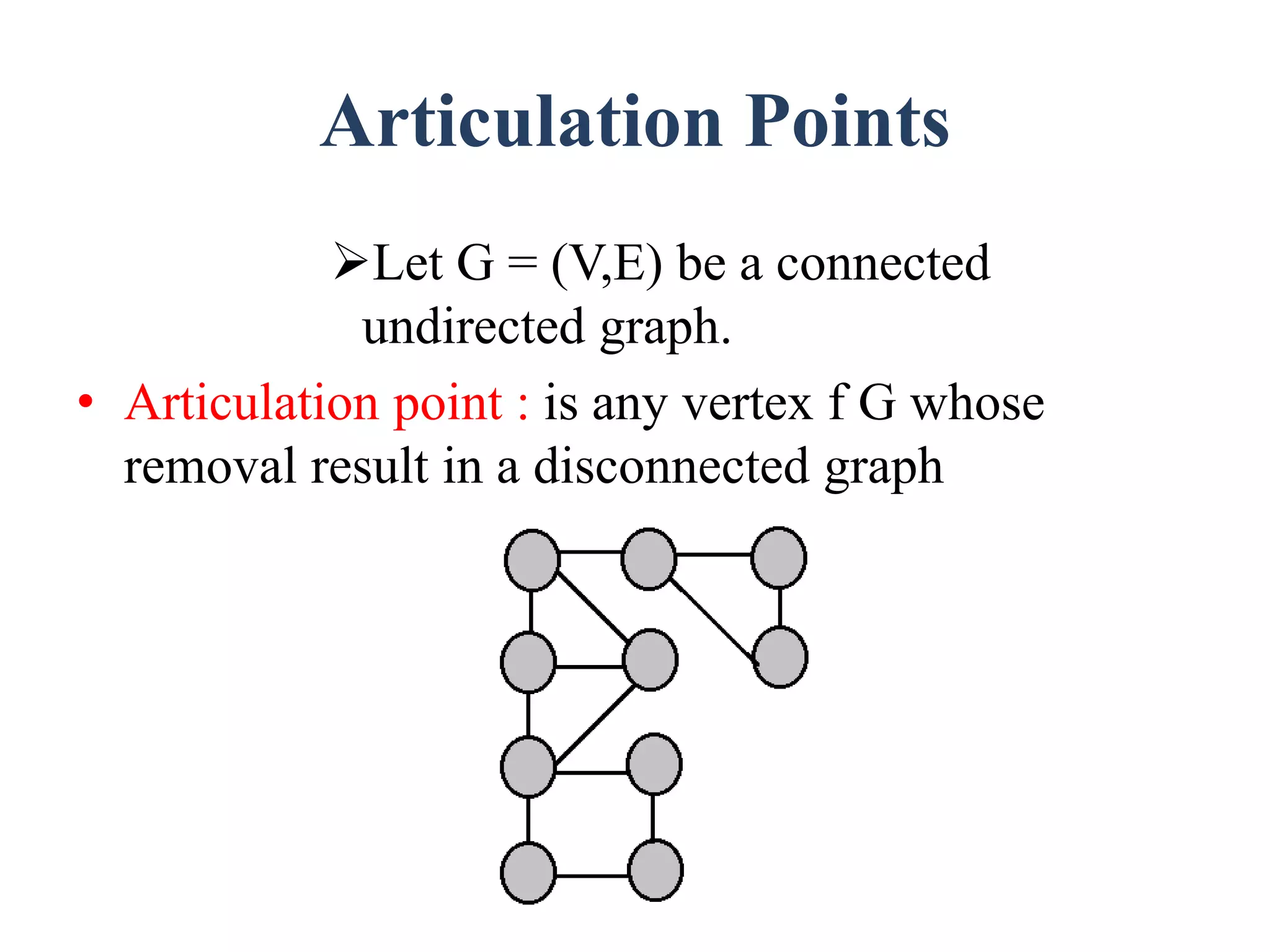
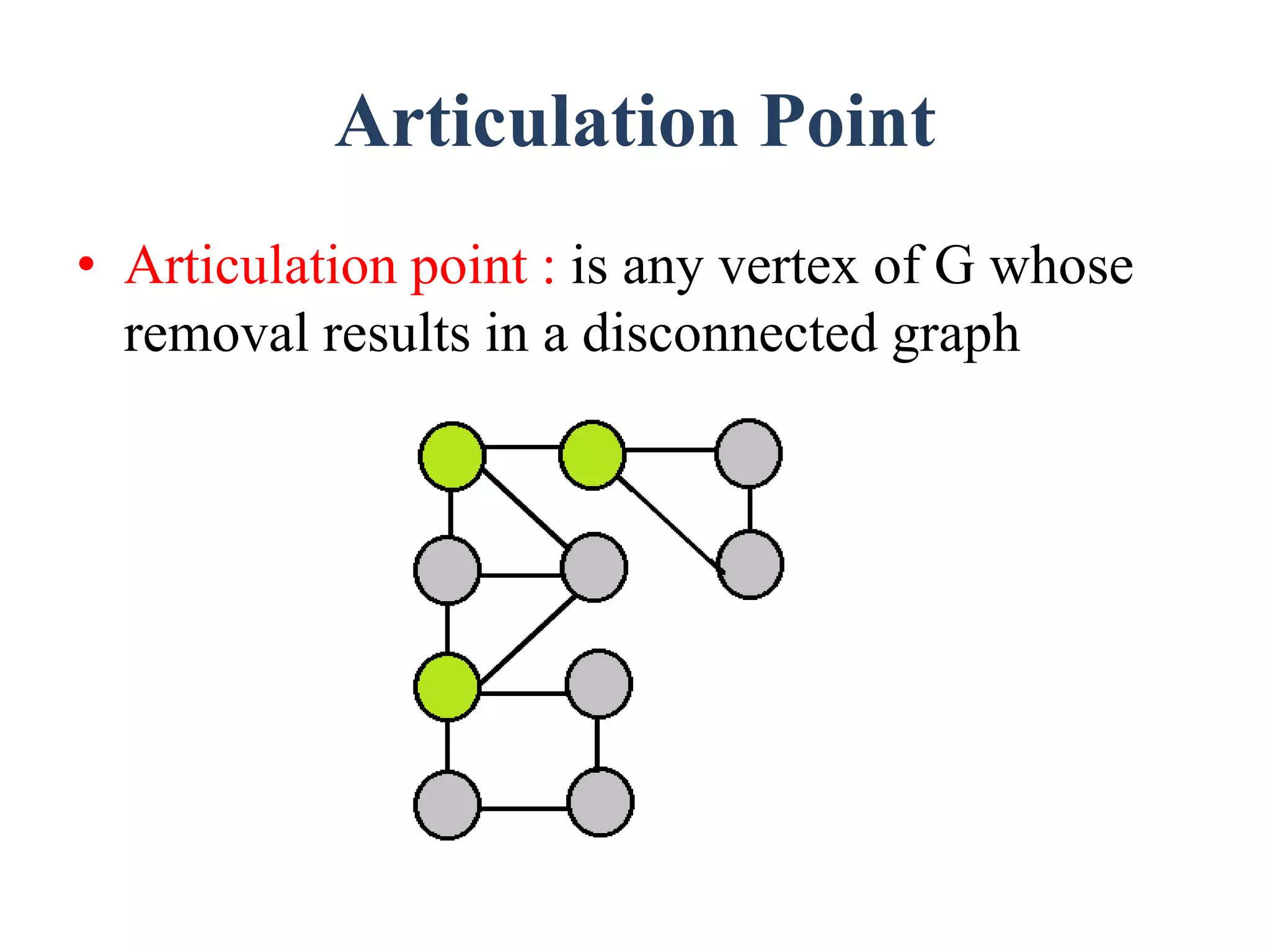
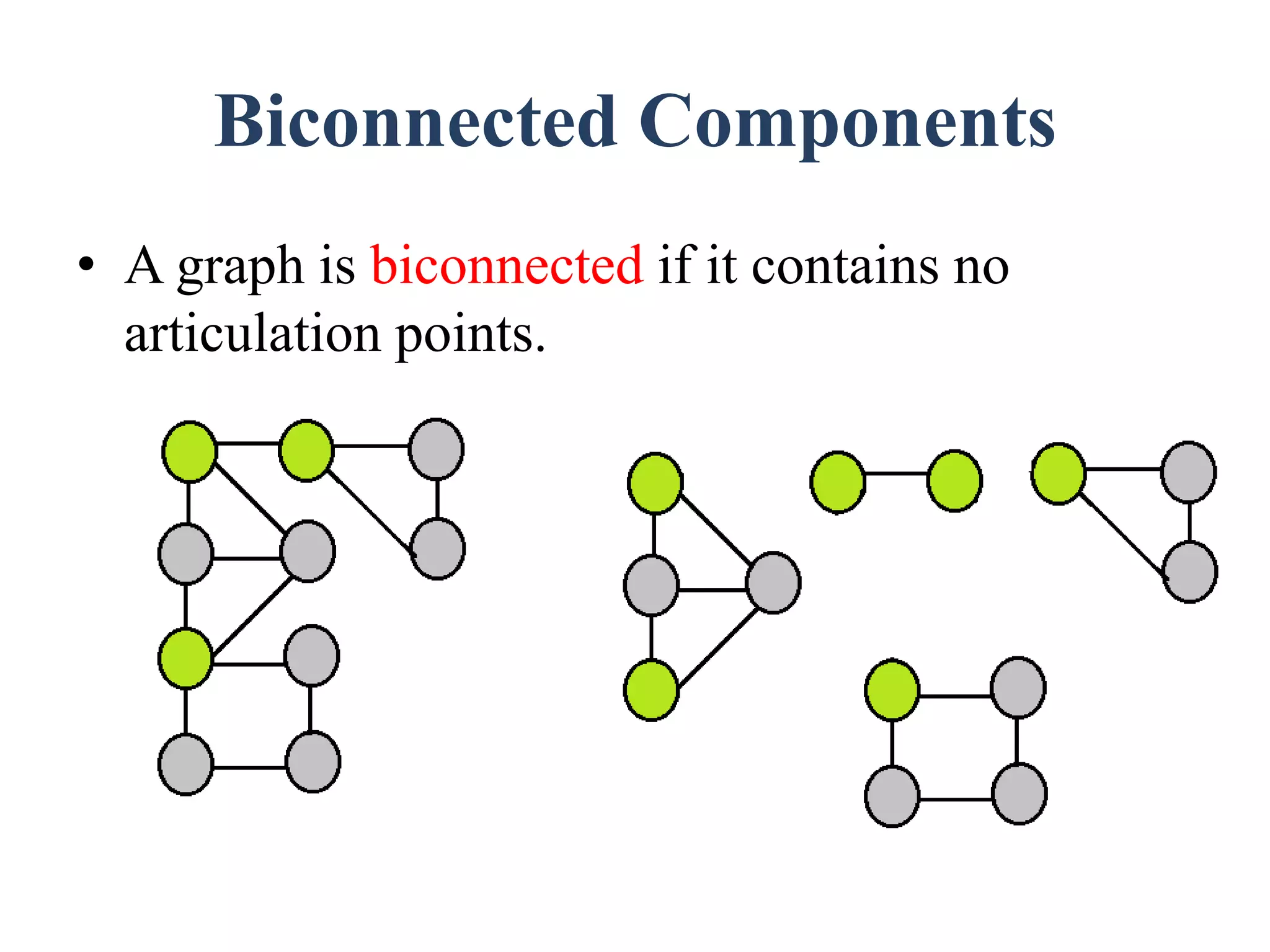
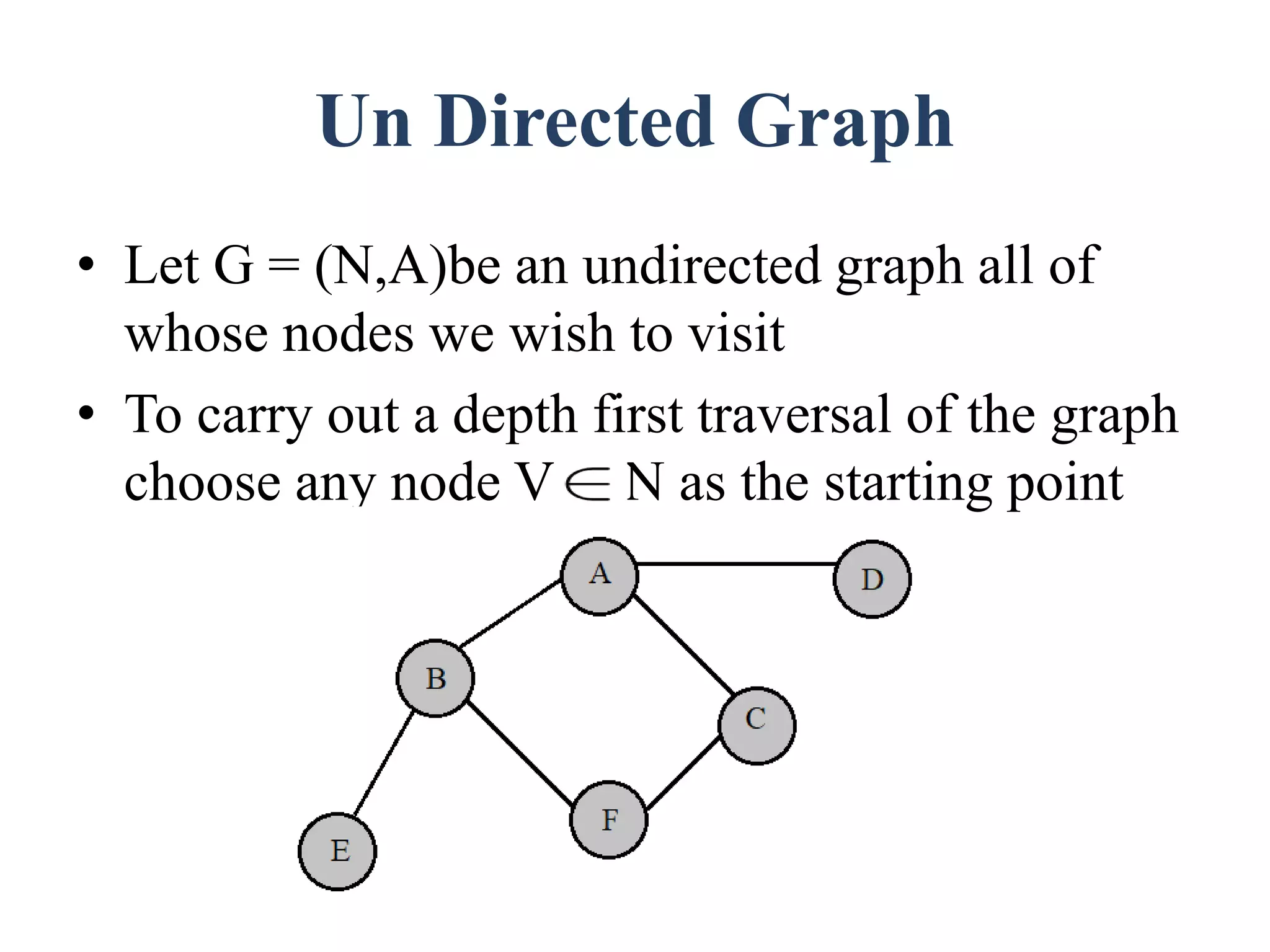
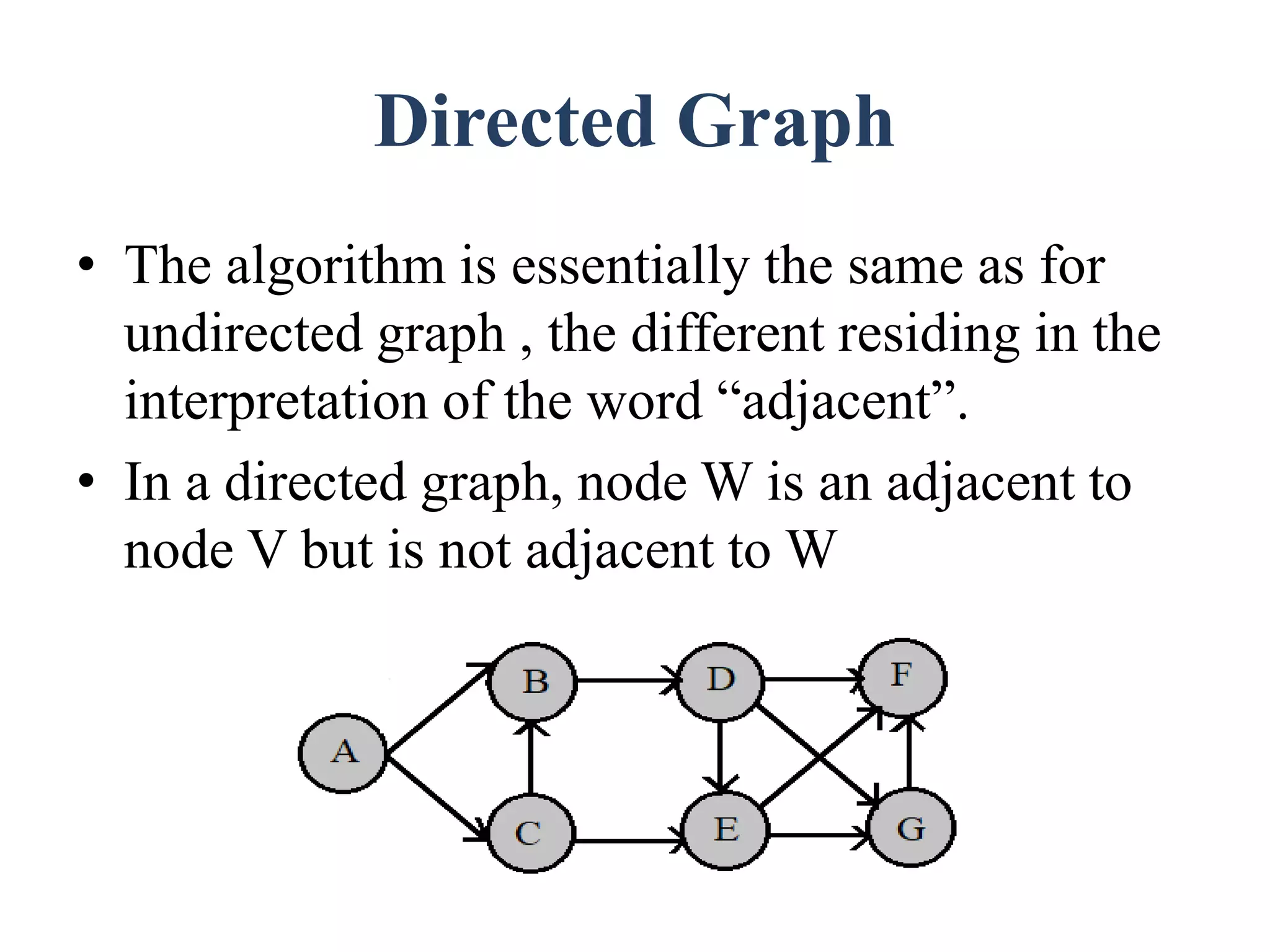
The document discusses graph theory concepts such as connected components, spanning trees, and biconnected components, with a focus on traversal and search techniques. It describes algorithms for depth-first search (DFS) and breadth-first search (BFS), as well as definitions of articulation points and the characteristics of spanning trees. Key points include how to identify connected components and implement traversal techniques effectively.

1. Basic Traversal And Search
Techniques
Presented by
S.Vijayalakshmi I-MSC[IT]

4. Connected Components
• A connected components is a subgraph in
which any two vertices are connected to each
other by paths and which is connected to no
additional vertices of the super graph

5. Algorithm For Connected
Components
• Connected components(G)
For each vertex V G
Make –set (V)
For each edge (U,V) G E
If find –set(4) find-set(V)
Union(U,V)
• Same Component(U,V)
If find-set(U)= =find-set(V)
Return true
Else return false

6. Determining Connected
Components
void Graph::Components()
{
visited = new Boolean[n];
for(int i=0 ; i<n ; i++)
visited[i]= False;
for(i=0 ; i<n ; i++)
if(!visited[i])
{
DFS(i);
OutputNewComponent();
}
delete[]vivited;
}

8. GRAPHS
• Graphs are one of the most interesting data
structures in computer science
• Graphs and tree are somewhat similar by their
structure and in fact tree is derived from the
graph and data structure
• Commonly used graph traversal algorithms
are:
DFS
BFS

9. BFS
• In this we visit the node level by
level so it will start with 0, which
is the root node then next ,then the
last level
• Queue is used to implement BFS
DFS
• In this we visit the root node first
then its children until it reaches
the end node
• Stack is used to implement DFS

10. Spanning Tree
• Spanning tree have a connected undirected graph
 connected : every node reachable from every other node
 Undirected: edges do not have automatic direction
• Spanning tree of the graph is a connected sub -
graph in which there are no cycles
• A spanning of a graph has no cycles but still
connects to every house
• If G is a connected graph with n vertices and m
edges, spanning tree of G must have n-1 edges ,
and no.of edges deleted from G to get a spanning
tree must be m -(n-1)=m-n+1

11. • A graph may have many spanning tree;for
instance the complete graph of four vertices.
A connected,
undirected graph
four of the spanning tree of the graph

13. Biconnected Components
Basically it is a graph theory.
A graph is biconnected if it contains no
‘articulation’ points .
A components of a graph G is maximal
“biconnected subgraph”. That means it is
not contained any larger biconnected
subgraph of G

14. Articulation Points
Let G = (V,E) be a connected
undirected graph.
• Articulation point : is any vertex f G whose
removal result in a disconnected graph

15. Articulation Point
• Articulation point : is any vertex of G whose
removal results in a disconnected graph

16. Biconnected Components
• A graph is biconnected if it contains no
articulation points.

18. Definition
• The aim of the DFS algorithm is travers the
graph in such a way that is try to go for from
the root node. Stack is use in the
implementation of the DFS. lets see hoe DFS
work with respect to the following graph.
• DFS – Depth First Search
• It implements stack, the concept of LIFO –
Last In First Out.

19. Un Directed Graph
• Let G = (N,A)be an undirected graph all of
whose nodes we wish to visit
• To carry out a depth first traversal of the graph
choose any node V N as the starting point

20. Directed Graph
• The algorithm is essentially the same as for
undirected graph , the different residing in the
interpretation of the word “adjacent”.
• In a directed graph, node W is an adjacent to
node V but is not adjacent to W