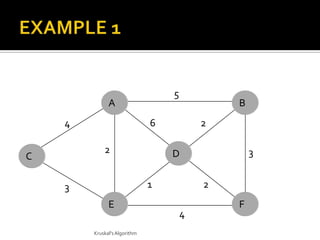
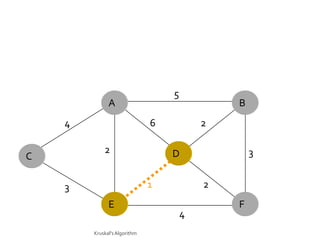
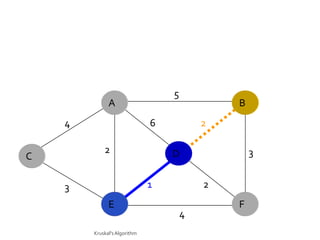
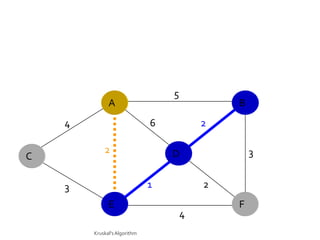
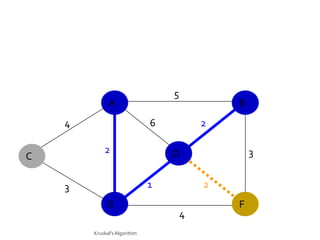
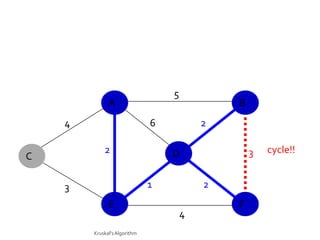
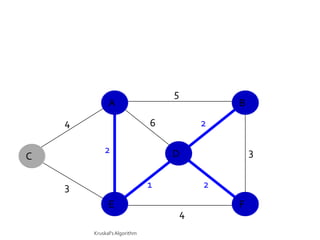
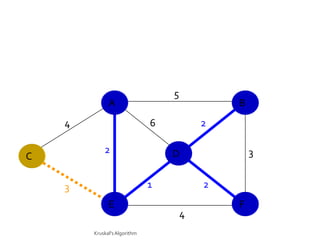
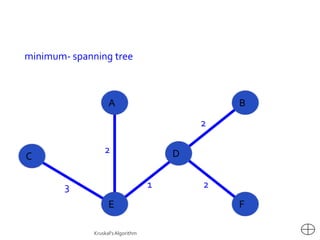
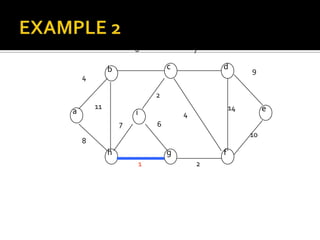
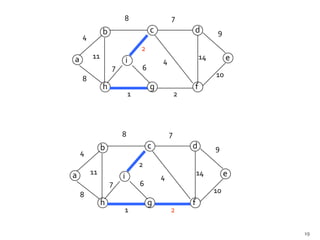
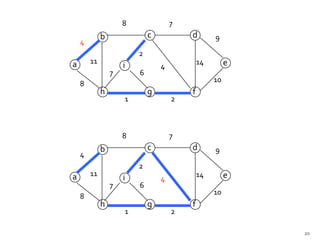
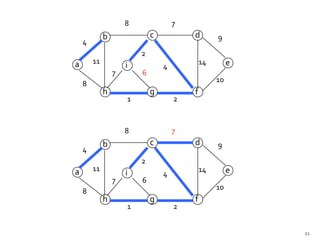
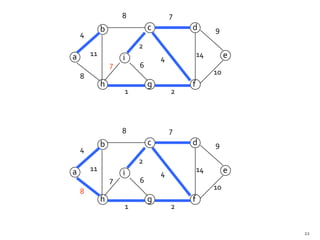
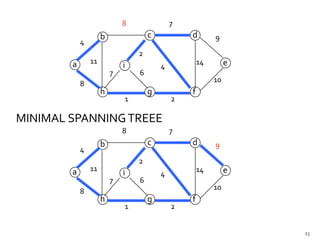
This document discusses the greedy algorithm approach for finding minimum spanning trees. It explains that greedy algorithms make locally optimal choices at each step to arrive at a global solution. Kruskal's algorithm is presented as an example greedy algorithm for finding minimum spanning trees. It works by sorting the edges by weight and then adding edges one by one if they do not form cycles. While greedy algorithms are faster, they do not always find the true optimal solution.

1. APPLICATION OF GREEDY METHOD
KRUSKAL’S ALGORITHM TO FIND
MINIMUM
COST SPANNING TREES

2.  An algorithm is a mathematical procedure often used to
solve optimization problems in a finite number of steps.
 Most solution algorithms make choices based on a
global overview of all current and future possibilities
aiming at reaching the single global optimum solution.
 Greedy algorithms make choices that look best at that
every moment.

3.  When compared to algorithms that guarantee to yield a
global optimum solution, greedy algorithms have
several advantages:
 They are easier to implement, they require much less
computing resources, they are much faster to execute.
 Their only disadvantage being that they do not always
reach the global optimum solution

4.  when the global optimum solution is not
reached, most of the times the reached sub- optimal
solution is a very good solution.
 Several classical optimization problems like minimum
spanning tree and optimal prefix codes for data
compression yield global optimum solutions using
greedy algorithm.

5.  A tree T is said to be a spanning tree of a connected
graph G if T is a subgraph of G and T contains all vertices
of G.
 Since the vertices of G are barely hanging together in a
spanning tree, it is a sort of skeleton of the original
graph g. so, a spanning tree is called a skeleton or
scaffolding of G.
 Among the spanning trees of G, one with the smallest
weight is called minimal spanning tree or shortest
spanning tree or shortest-distance spanning tree.

6. A second greedy algorithm was developed by Joseph Kruskal.
Steps in Kruskal’s algorithm:
 list all edges of G in order of increasing weight.
 Select a smallest edge of G.
 For each successive step, select (from all remaining
edges of G) another smallest edge that makes no circuit
 with the previously selected edges.
 Continue until n-1 edges have been selected.

7.  At each stage, the algorithm chooses an edge
to add to its current partial solution. To do so, it needs
to test each candidate edge (u ,v ) to
see whether the endpoints u and v lie in different
components; otherwise the edge produces a
cycle.

8. 5
A B
4 6 2
2 D 3
C
3 1 2
E F
4
Kruskal's Algorithm

9. enqueue edges of G in a queue in increasing order of
cost.
T=;
while(queue is not empty)
{
dequeue an edge e;
if(e does not create a cycle with edges in T)
add e to T;
}
return T;

10. 5
A B
4 6 2
2 D 3
C
3 1 2
E F
4
Kruskal's Algorithm

11. 5
A B
4 6 2
2 D 3
C
3 1 2
E F
4
Kruskal's Algorithm

12. 5
A B
4 6 2
2 D 3
C
3 1 2
E F
4
Kruskal's Algorithm

13. 5
A B
4 6 2
2 D 3
C
3 1 2
E F
4
Kruskal's Algorithm

14. 5
A B
4 6 2
2 D 3 cycle!!
C
3 1 2
E F
4
Kruskal's Algorithm

15. 5
A B
4 6 2
2 D 3
C
3 1 2
E F
4
Kruskal's Algorithm

16. 5
A B
4 6 2
2 D 3
C
3 1 2
E F
4
Kruskal's Algorithm

17. minimum- spanning tree
A B
2
2 D
C
3 1 2
E F
Kruskal's Algorithm

18. 8 7
b c d 9
4
2
11 14 e
a i 4
7 6
10
8
h g f
1 2

19. 8 7
b c d 9
4
2
a 11 14 e
i 4
7 6
10
8
h g f
1 2
8 7
b c d 9
4
2
a 11 14 e
i 4
7 6
10
8
h g f
1 2
19

20. 8 7
b c d 9
4
2
a 11 14 e
i 4
7 6
10
8
h g f
1 2
8 7
b c d 9
4
2
a 11 14 e
i 4
7 6
10
8
h g f
1 2
20

21. 8 7
b c d 9
4
2
a 11 14 e
i 4
7 6
10
8
h g f
1 2
8 7
b c d 9
4
2
a 11 14 e
i 4
7 6
10
8
h g f
1 2
21

22. 8 7
b c d 9
4
2
a 11 14 e
i 4
7 6
10
8
h g f
1 2
8 7
b c d 9
4
2
a 11 14 e
i 4
7 6
10
8
h g f
1 2
22

23. 8 7
b c d 9
4
2
a 11 14 e
i 4
7 6
10
8
h g f
1 2
MINIMAL SPANNING TREEE
8 7
b c d 9
4
2
a 11 14 e
i 4
7 6
10
8
h g f
1 2
23

24.  Initialization O(V) time
 Sorting the edges Q(E lg E) = Q(E lg V) (why?)
 O(E) calls to FindSet
 Union costs
 Let t(v) – the number of times v is moved to a new
cluster
 Each time a vertex is moved to a new cluster the size
of the cluster containing the vertex at least doubles:
t(v) log V
 Total time spent doing Union vV
 t (v)  V log V
 Total time: O(E lg V)
24

25.  Where ever the minimum distance is needed to achieve
there this algorithm gets place.
 For example.
 In telephone lining under the ground, they have to connect all
the cities with the minimum amount of wire.
 If the new connection is in position to add between cities, there
we have to consider the minimum cost distance.
 Assume, if the minimum distance is not calculated, the wastage
of wires will be in peak.

26.  Railways track construction.
 National highway construction.
 Flyover bridge construction.
 Network between two intranets.
 The another non-technical example will be as,
 The by-pass rider or point to point buses will move on with the
minimum distance path to reach the destination much faster.
They will never circulate their bus through unwanted towns and
villages.