The Koch Snowflake SELF SIMILAR CONCEPTS

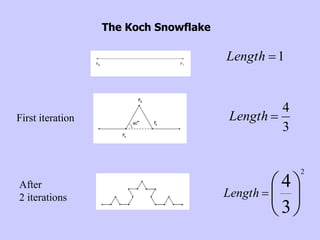
The Koch Snowflake
3
4

Length
1

Length







3
4
2
Length
First iteration
After
2 iterations

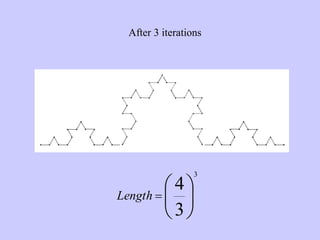
After 3 iterations







3
4
3
Length

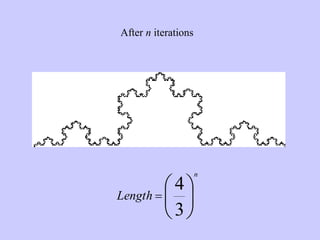
After n iterations







3
4
n
Length



 






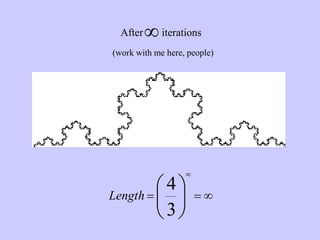
3
4
Length
After iterations

(work with me here, people)

The Koch snowflake is six of these put together to form . . .
. . . well, a snowflake.

Notice that the perimeter of the Koch snowflake is infinite . . .
. . . but that the area it bounds is finite (indeed, it is
contained in the white square).

The Koch snowflake has even been used in technology:
Boston - Mar 13, 2002
Fractal Antenna Systems, Inc. today disclosed that it has
filed for patent protection on a new class of antenna arrays
that use close-packed arrangements of fractal elements to
get superior performance characteristics.
Fractal Tiling Arrays -- Firm Reports
Breakthrough in Array Antennas

Each of the six sides of the Koch snowflake is
self-similar: If you take a small copy of it . . .
. . . then dilate by a factor of 3 . . .
. . . you get four copies of the original.

But self-similarity is not what makes the Koch snowflake
a fractal! (Contrary to a common misconception.)
After all, many common geometric objects exhibit
self-similarity. Consider, for example, the humble
square.

If you take a small square . . .
. . . and dilate by a factor of 2 . . .
. . . then you get 4 copies of the original.
A square is self-similar, but it most certainly is not a fractal.

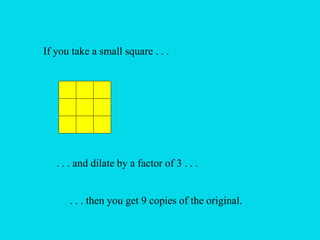
If you take a small square . . .
. . . and dilate by a factor of 3 . . .
. . . then you get 9 copies of the original.

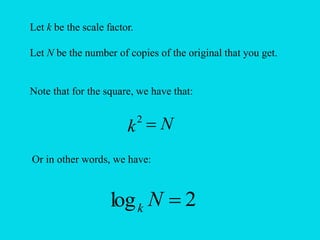
Let k be the scale factor.
Let N be the number of copies of the original that you get.
Note that for the square, we have that:
2
log 
N
k
N
k 
2
Or in other words, we have:

Let’s compute N
k
log for some other shapes.

Line segment
Original
Dilated
k = scale factor = 2
N = number of copies of original = 2
1
log 
N
k

Triangle
Original Dilated
2
log 
N
k

Cube
Original Dilated
3
log 
N
k

Shape
Square 2
Line segment 1
Triangle 2
Cube 3
N
k
log
What does N
k
log tell us about a shape?

That’s right: N
k
log tells us the dimension of the shape.
(Note that for this to make sense, the shape has to be
self-similar.)
So for a self-similar shape, we can take N
k
log
to be the definition of its dimension.
(It turns out that this definition coincides with a much more
general definition of dimension called the fractal dimension.)

Now let’s recall what k and N were for one side of the
Koch snowflake:
...
261
.
1
4
log
log 3 

N
k

So each side of the Koch snowflake is approximately
1.261-dimensional.
That’s what makes the Koch snowflake a fractal – the fact that
its dimension is not an integer.
Even shapes which are not self-similar can be fractals. The
most famous of these is the Mandelbrot set.

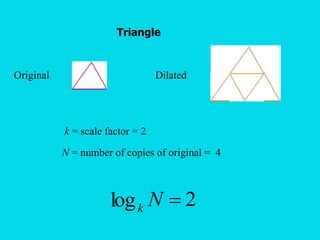
Start with a line segment of length 1.
Now cut away the middle third.
Then cut away the middle third of each remaining piece.
]
1
,
0
[
1 
C
Iterate.
]
1
,
3
2
[
]
3
1
,
0
[
2 

C
. . . . . .












 ]
1
,
9
8
[
]
9
7
,
3
2
[
]
3
1
,
9
2
[
]
9
1
,
0
[
3 


C







 







 







]
1
,
3
1
3
[
]
3
2
3
,
3
2
[
...
]
3
1
,
3
2
[
]
3
1
,
0
[ 1
2
1
2
2
2
1
1 n
n
n
n
n
n
n
n
n
C 




The Cantor set is what’s left after you’re finished cutting.
In other words:




1
n
n
C
C = Cantor set

We can ask several questions about the Cantor set, such as:
• What is its cardinality?
• What is its length? Indeed, does the concept of length
apply to it?
• Between any two points in the Cantor set, can you
find another point in the Cantor set?
• Is it complete?
• What is its fractal dimension?

If you take the Cantor set . . .
. . . and dilate by a factor of k = 3 . . .
. . . then you get N = 2 copies of the original.
...
63
.
0
2
log
log 3 

N
k

So the Cantor set is approximately 0.63-dimensional.

Start with a square of side length 3, with a square of side
length 1 removed from its center.
perimeter = 4(3) + 4(1)
area = 1
3
2
2


Think of this shape as consisting of eight small squares, each
of side length 1.
area = 








3
1
8
1
3
2
2
2
From each small square, remove its central square.
perimeter =
3
1
4
8
1
4
3
4 






Iterate.
1
4
3
4 


perimeter =
1
3
2
2

area =

perimeter =
perimeter =
3
1
4
8
1
4
3
4 














3
1
8
1
3
2
2
2
area =
Iterate.

perimeter = 














3
1
4
8
3
1
4
8
1
4
3
4
2
2
area = 

















3
1
8
3
1
8
1
3
2
2
2
2
2
2
Iterate.




























3
1
8
3
1
8
3
1
8
1
3
3
2
3
2
2
2
2
2
2
area =
























3
1
4
8
3
1
4
8
3
1
4
8
1
4
3
4
3
3
2
2
perimeter =
Iterate.

Like the Cantor set, the Sierpinski carpet is what’s left after
you’re finished removing everything.
In other words, it’s the intersection of all the previous sets.

...
3
1
4
8
3
1
4
8
3
1
4
8
1
4
3
4
3
3
2
2

























perimeter =













0 3
8
4
3
4
n
n



...
3
1
8
3
1
8
3
1
8
1
3
3
2
3
2
2
2
2
2
2




























area =

























 ...
9
8
9
8
9
8
1
3
3
2
2















9
8
1
3
1
2
= 0

So the Sierpinski carpet has an infinite perimeter – but
it bounds a region with an area of zero!
Weird

Your turn: compute the fractal dimension of the Sierpinski carpet.
89
.
1
8
log3 

The Sierpinski carpet has a 3-dimensional analogue called
the Menger sponge.

Its surface area is infinite, yet it bounds a region of zero volume.

The fractal dimension of the Menger sponge is:
73
.
2
20
log3 

The Koch Snowflake SELF SIMILAR CONCEPTS

More Related Content

Similar to The Koch Snowflake SELF SIMILAR CONCEPTS

More from JauwadSyed

Recently uploaded

The Koch Snowflake SELF SIMILAR CONCEPTS