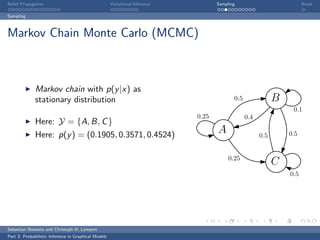
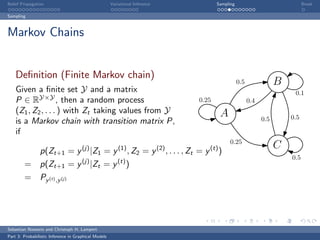
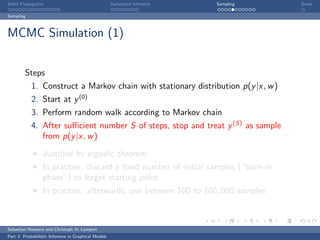
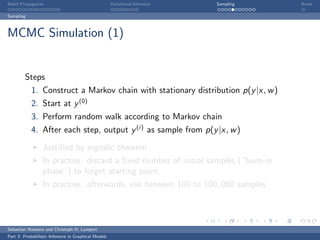
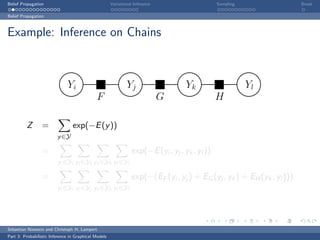
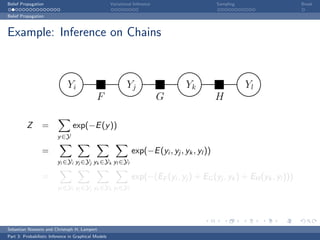
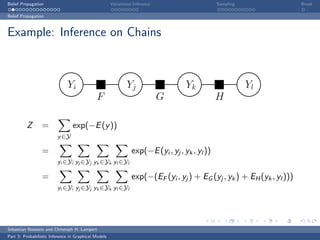
This document discusses belief propagation for probabilistic inference in graphical models. It provides an example of applying belief propagation to inference on a chain-structured graph. Belief propagation breaks the computation into message passing between nodes, allowing the inference to be computed by multiplying messages along the edges. This results in a closed form solution that avoids expensive computations over all joint assignments.

1. Belief Propagation Variational Inference Sampling Break
Part 3: Probabilistic Inference in
Graphical Models
Sebastian Nowozin and Christoph H. Lampert
Colorado Springs, 25th June 2011
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

2. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Belief Propagation
“Message-passing” algorithm
Exact and optimal for tree-structured graphs
Approximate for cyclic graphs
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

3. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Example: Inference on Chains
Yi Yj Yk Yl
F G H
Z = exp(−E (y ))
y ∈Y
= exp(−E (yi , yj , yk , yl ))
yi ∈Yi yj ∈Yj yk ∈Yk yl ∈Yl
= exp(−(EF (yi , yj ) + EG (yj , yk ) + EH (yk , yl )))
yi ∈Yi yj ∈Yj yk ∈Yk yl ∈Yl
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

4. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Example: Inference on Chains
Yi Yj Yk Yl
F G H
Z = exp(−E (y ))
y ∈Y
= exp(−E (yi , yj , yk , yl ))
yi ∈Yi yj ∈Yj yk ∈Yk yl ∈Yl
= exp(−(EF (yi , yj ) + EG (yj , yk ) + EH (yk , yl )))
yi ∈Yi yj ∈Yj yk ∈Yk yl ∈Yl
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

5. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Example: Inference on Chains
Yi Yj Yk Yl
F G H
Z = exp(−E (y ))
y ∈Y
= exp(−E (yi , yj , yk , yl ))
yi ∈Yi yj ∈Yj yk ∈Yk yl ∈Yl
= exp(−(EF (yi , yj ) + EG (yj , yk ) + EH (yk , yl )))
yi ∈Yi yj ∈Yj yk ∈Yk yl ∈Yl
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

6. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Example: Inference on Chains
Yi Yj Yk Yl
F G H
Z = exp(−(EF (yi , yj ) + EG (yj , yk ) + EH (yk , yl )))
yi ∈Yi yj ∈Yj yk ∈Yk yl ∈Yl
= exp(−EF (yi , yj )) exp(−EG (yj , yk )) exp(−EH (yk , yl ))
yi ∈Yi yj ∈Yj yk ∈Yk yl ∈Yl
= exp(−EF (yi , yj )) exp(−EG (yj , yk )) exp(−EH (yk , yl ))
yi ∈Yi yj ∈Yj yk ∈Yk yl ∈Yl
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

7. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Example: Inference on Chains
Yi Yj Yk Yl
F G H
Z = exp(−(EF (yi , yj ) + EG (yj , yk ) + EH (yk , yl )))
yi ∈Yi yj ∈Yj yk ∈Yk yl ∈Yl
= exp(−EF (yi , yj )) exp(−EG (yj , yk )) exp(−EH (yk , yl ))
yi ∈Yi yj ∈Yj yk ∈Yk yl ∈Yl
= exp(−EF (yi , yj )) exp(−EG (yj , yk )) exp(−EH (yk , yl ))
yi ∈Yi yj ∈Yj yk ∈Yk yl ∈Yl
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

8. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Example: Inference on Chains
Yi Yj Yk Yl
F G H
Z = exp(−(EF (yi , yj ) + EG (yj , yk ) + EH (yk , yl )))
yi ∈Yi yj ∈Yj yk ∈Yk yl ∈Yl
= exp(−EF (yi , yj )) exp(−EG (yj , yk )) exp(−EH (yk , yl ))
yi ∈Yi yj ∈Yj yk ∈Yk yl ∈Yl
= exp(−EF (yi , yj )) exp(−EG (yj , yk )) exp(−EH (yk , yl ))
yi ∈Yi yj ∈Yj yk ∈Yk yl ∈Yl
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

9. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Example: Inference on Chains
rH→Yk ∈ RYk
Yi Yj Yk Yl
F G H
Z = exp(−EF (yi , yj )) exp(−EG (yj , yk )) exp(−EH (yk , yl ))
yi ∈Yi yj ∈Yj yk ∈Yk yl ∈Yl
rH→Yk (yk )
= exp(−EF (yi , yj )) exp(−EG (yj , yk ))rH→Yk (yk )
yi ∈Yi yj ∈Yj yk ∈Yi
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

10. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Example: Inference on Chains
rH→Yk ∈ RYk
Yi Yj Yk Yl
F G H
Z = exp(−EF (yi , yj )) exp(−EG (yj , yk )) exp(−EH (yk , yl ))
yi ∈Yi yj ∈Yj yk ∈Yk yl ∈Yl
rH→Yk (yk )
= exp(−EF (yi , yj )) exp(−EG (yj , yk ))rH→Yk (yk )
yi ∈Yi yj ∈Yj yk ∈Yi
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

11. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Example: Inference on Chains
rG→Yj ∈ RYj
Yi Yj Yk Yl
F G H
Z = exp(−EF (yi , yj )) exp(−EG (yj , yk ))rH→Yk (yk )
yi ∈Yi yj ∈Yj yk ∈Yk
rG →Yj (yj )
= exp(−EF (yi , yj ))rG →Yj (yj )
yi ∈Yi yj ∈Yj
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

12. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Example: Inference on Chains
rG→Yj ∈ RYj
Yi Yj Yk Yl
F G H
Z = exp(−EF (yi , yj )) exp(−EG (yj , yk ))rH→Yk (yk )
yi ∈Yi yj ∈Yj yk ∈Yk
rG →Yj (yj )
= exp(−EF (yi , yj ))rG →Yj (yj )
yi ∈Yi yj ∈Yj
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

13. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Example: Inference on Trees
Yi Yj Yk Yl
F G H
I
Ym
Z = exp(−E (y ))
y ∈Y
= exp(−(EF (yi , yj ) + · · · + EI (yk , ym )))
yi ∈Yi yj ∈Yi yk ∈Yi yl ∈Yi ym ∈Ym
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

14. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Example: Inference on Trees
Yi Yj Yk Yl
F G H
I
Ym
Z = exp(−EF (yi , yj )) exp(−EG (yj , yk )) ·
yi ∈Yi yj ∈Yj yk ∈Yk
 
   
 
 
 exp(−EH (yk , yl ))· exp(−EI (yk , ym )) 


 yl ∈Yl ym ∈Ym 
 
rH→Yk (yk ) rI →Yk (yk )
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

15. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Example: Inference on Trees
rH→Yk (yk )
Yi Yj Yk Yl
F G H
rI→Yk (yk ) I
Ym
Z = exp(−EF (yi , yj )) exp(−EG (yj , yk )) ·
yi ∈Yi yj ∈Yj yk ∈Yk
(rH→Yk (yk ) · rI →Yk (yk ))
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

16. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Example: Inference on Trees
qYk →G (yk ) rH→Yk (yk )
Yi Yj Yk Yl
F G H
rI→Yk (yk ) I
Ym
Z = exp(−EF (yi , yj )) exp(−EG (yj , yk )) ·
yi ∈Yi yj ∈Yj yk ∈Yk
(rH→Yk (yk ) · rI →Yk (yk ))
qYk →G (yk )
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

17. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Example: Inference on Trees
qYk →G (yk ) rH→Yk (yk )
Yi Yj Yk Yl
F G H
rI→Yk (yk ) I
Ym
Z = exp(−EF (yi , yj )) exp(−EG (yj , yk ))qYk →G (yk )
yi ∈Yi yj ∈Yj yk ∈Yk
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

18. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Factor Graph Sum-Product Algorithm
“Message”: pair of vectors at each ...
factor graph edge (i, F ) ∈ E ... rF →Yi
1. rF →Yi ∈ RYi : factor-to-variable
Yi ...
message
2. qYi →F ∈ RYi : variable-to-factor ... F
qYi →F
message
Algorithm iteratively update messages
After convergence: Z and µF can be
obtained from the messages
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

19. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Factor Graph Sum-Product Algorithm
“Message”: pair of vectors at each ...
factor graph edge (i, F ) ∈ E ... rF →Yi
1. rF →Yi ∈ RYi : factor-to-variable
Yi ...
message
2. qYi →F ∈ RYi : variable-to-factor ... F
qYi →F
message
Algorithm iteratively update messages
After convergence: Z and µF can be
obtained from the messages
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

20. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Sum-Product: Variable-to-Factor message
Set of factors adjacent to
rA→Yi
variable i A qYi →F
M(i) = {F ∈ F : (i, F ) ∈ E} Yi
B rF →Yi F
Variable-to-factor message . rB→Yi
.
.
qYi →F (yi ) = rF →Yi (yi )
F ∈M(i){F }
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

21. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Sum-Product: Factor-to-Variable message
Yj qYj →F
rF →Yi
Yi
Yk qYi →F
qYk →F F
.
.
.
Factor-to-variable message
 
rF →Yi (yi ) = exp (−EF (yF )) qYj →F (yj )
yF ∈YF , j∈N(F ){i}
yi =yi
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

22. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Message Scheduling
qYi →F (yi ) = rF →Yi (yi )
F ∈M(i){F }
 
rF →Yi (yi ) = exp (−EF (yF )) qYj →F (yj )
yF ∈YF , j∈N(F ){i}
yi =yi
Problem: message updates depend on each other
No dependencies if product is empty (= 1)
For tree-structured graphs we can resolve all dependencies
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

23. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Message Scheduling
qYi →F (yi ) = rF →Yi (yi )
F ∈M(i){F }
 
rF →Yi (yi ) = exp (−EF (yF )) qYj →F (yj )
yF ∈YF , j∈N(F ){i}
yi =yi
Problem: message updates depend on each other
No dependencies if product is empty (= 1)
For tree-structured graphs we can resolve all dependencies
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

24. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Message Scheduling
qYi →F (yi ) = rF →Yi (yi )
F ∈M(i){F }
 
rF →Yi (yi ) = exp (−EF (yF )) qYj →F (yj )
yF ∈YF , j∈N(F ){i}
yi =yi
Problem: message updates depend on each other
No dependencies if product is empty (= 1)
For tree-structured graphs we can resolve all dependencies
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

25. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Message Scheduling: Trees
10. 1.
B Ym B Ym
9. 2.
F F
6. 8. 5. 3.
C C
Yk Yl Yk Yl
7. 4.
3. 5. 8. 6.
D E D E
2. 4. 9. 7.
A A
Yi Yj Yi Yj
1. 10.
1. Select one variable node as tree root
2. Compute leaf-to-root messages
3. Compute root-to-leaf messages
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

26. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Inference Results: Z and marginals .
.
.
.
.
.
Yi
A
rA→Yi qYi →F
...
F
Yi qYj →F qYk →F
rB→Yi rC→Yi
B C Yj Yk
... ... ... ... ... ...
Partition function, evaluated at root
Z= rF →Yr (yr )
yr ∈Yr F ∈M(r )
Marginal distributions, for each factor
1
µF (yF ) = p(YF = yF ) = exp (−EF (yF )) qYi →F (yi )
Z
i∈N(F )
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

27. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Max-Product/Max-Sum Algorithm
Belief Propagation for MAP inference
y ∗ = argmax p(Y = y |x, w )
y ∈Y
Exact for trees
For cyclic graphs: not as well understood as sum-product algorithm
qYi →F (yi ) = rF →Yi (yi )
F ∈M(i){F }
 
rF →Yi (yi ) = max −EF (yF ) + qYj →F (yj )
yF ∈YF ,
j∈N(F ){i}
yi =yi
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

28. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Sum-Product/Max-Sum comparison
Sum-Product
qYi →F (yi ) = rF →Yi (yi )
F ∈M(i){F }
 
rF →Yi (yi ) = exp (−EF (yF )) qYj →F (yj )
yF ∈YF , j∈N(F ){i}
yi =yi
Max-Sum
qYi →F (yi ) = rF →Yi (yi )
F ∈M(i){F }
 
rF →Yi (yi ) = max −EF (yF ) + qYj →F (yj )
yF ∈YF ,
j∈N(F ){i}
yi =yi
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

29. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Example: Pictorial Structures
(1)
Ftop
X Ytop
(2)
F
top,head
... ...
Yhead
... ...
...
Yrarm Ytorso Ylarm
...
Yrhnd
... ... ... Ylhnd
Yrleg Ylleg
... ...
Yrfoot Ylfoot
Tree-structured model for articulated pose (Felzenszwalb and
Huttenlocher, 2000), (Fischler and Elschlager, 1973)
Body-part variables, states: discretized tuple (x, y , s, θ)
(x, y ) position, s scale, and θ rotation
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

30. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Example: Pictorial Structures
(1)
Ftop
X Ytop
(2)
F
top,head
... ...
Yhead
... ...
...
Yrarm Ytorso Ylarm
...
Yrhnd
... ... ... Ylhnd
Yrleg Ylleg
... ...
Yrfoot Ylfoot
Tree-structured model for articulated pose (Felzenszwalb and
Huttenlocher, 2000), (Fischler and Elschlager, 1973)
Body-part variables, states: discretized tuple (x, y , s, θ)
(x, y ) position, s scale, and θ rotation
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

31. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Example: Pictorial Structures (cont)
 
rF →Yi (yi ) = max −EF (yi , yj ) + qYj →F (yj ) (1)
(yi ,yj )∈Yi ×Yj ,
j∈N(F ){i}
yi =yi
Because Yi is large (≈ 500k), Yi × Yj is too big
(Felzenszwalb and Huttenlocher, 2000) use special form for
EF (yi , yj ) so that (1) is computable in O(|Yi |)
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

32. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Loopy Belief Propagation
Key difference: no schedule that removes dependencies
But: message computation is still well defined
Therefore, classic loopy belief propagation (Pearl, 1988)
1. Initialize message vectors to 1 (sum-product) or 0 (max-sum)
2. Update messages, hoping for convergence
3. Upon convergence, treat beliefs µF as approximate marginals
Different messaging schedules (synchronous/asynchronous,
static/dynamic)
Improvements: generalized BP (Yedidia et al., 2001), convergent BP
(Heskes, 2006)
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

33. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Loopy Belief Propagation
Key difference: no schedule that removes dependencies
But: message computation is still well defined
Therefore, classic loopy belief propagation (Pearl, 1988)
1. Initialize message vectors to 1 (sum-product) or 0 (max-sum)
2. Update messages, hoping for convergence
3. Upon convergence, treat beliefs µF as approximate marginals
Different messaging schedules (synchronous/asynchronous,
static/dynamic)
Improvements: generalized BP (Yedidia et al., 2001), convergent BP
(Heskes, 2006)
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

34. Belief Propagation Variational Inference Sampling Break
Belief Propagation
Synchronous Iteration
A B A B
Yi Yj Yk Yi Yj Yk
C D E C D E
F G F G
Yl Ym Yn Yl Ym Yn
H I J H I J
K L K L
Yo Yp Yq Yo Yp Yq
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

35. Belief Propagation Variational Inference Sampling Break
Variational Inference
Mean field methods
Mean field methods (Jordan et al., 1999), (Xing et al., 2003)
Distribution p(y |x, w ), inference intractable
Approximate distribution q(y )
Tractable family Q
Q
q
p
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

36. Belief Propagation Variational Inference Sampling Break
Variational Inference
Mean field methods (cont)
Q
q ∗ = argmin DKL (q(y ) p(y |x, w ))
q∈Q
q
p
DKL (q(y ) p(y |x, w ))
q(y )
= q(y ) log
p(y |x, w )
y ∈Y
= q(y ) log q(y ) − q(y ) log p(y |x, w )
y ∈Y y ∈Y
= −H(q) + µF ,yF (q)EF (yF ; xF , w ) + log Z (x, w ),
F ∈F yF ∈YF
where H(q) is the entropy of q and µF ,yF are the marginals of q. (The
form of µ depends on Q.)
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

37. Belief Propagation Variational Inference Sampling Break
Variational Inference
Mean field methods (cont)
Q
q ∗ = argmin DKL (q(y ) p(y |x, w ))
q∈Q
q
p
DKL (q(y ) p(y |x, w ))
q(y )
= q(y ) log
p(y |x, w )
y ∈Y
= q(y ) log q(y ) − q(y ) log p(y |x, w )
y ∈Y y ∈Y
= −H(q) + µF ,yF (q)EF (yF ; xF , w ) + log Z (x, w ),
F ∈F yF ∈YF
where H(q) is the entropy of q and µF ,yF are the marginals of q. (The
form of µ depends on Q.)
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

38. Belief Propagation Variational Inference Sampling Break
Variational Inference
Mean field methods (cont)
q ∗ = argmin DKL (q(y ) p(y |x, w ))
q∈Q
When Q is rich: q ∗ is close to p
Marginals of q ∗ approximate marginals of p
Gibbs inequality
DKL (q(y ) p(y |x, w )) ≥ 0
Therefore, we have a lower bound
log Z (x, w ) ≥ H(q) − µF ,yF (q)EF (yF ; xF , w ).
F ∈F yF ∈YF
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

39. Belief Propagation Variational Inference Sampling Break
Variational Inference
Mean field methods (cont)
q ∗ = argmin DKL (q(y ) p(y |x, w ))
q∈Q
When Q is rich: q ∗ is close to p
Marginals of q ∗ approximate marginals of p
Gibbs inequality
DKL (q(y ) p(y |x, w )) ≥ 0
Therefore, we have a lower bound
log Z (x, w ) ≥ H(q) − µF ,yF (q)EF (yF ; xF , w ).
F ∈F yF ∈YF
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

40. Belief Propagation Variational Inference Sampling Break
Variational Inference
Naive Mean Field
Set Q all distributions of the form
q(y ) = qi (yi ).
i∈V
qe qf qg
qh qi qj
qk ql qm
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

41. Belief Propagation Variational Inference Sampling Break
Variational Inference
Naive Mean Field
Set Q all distributions of the form
q(y ) = qi (yi ).
i∈V
Marginals µF ,yF take the form
µF ,yF (q) = qi (yi ).
i∈N(F )
Entropy H(q) decomposes
H(q) = Hi (qi ) = − qi (yi ) log qi (yi ).
i∈V i∈V yi ∈Yi
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

42. Belief Propagation Variational Inference Sampling Break
Variational Inference
Naive Mean Field (cont)
Putting it together,
argmin DKL (q(y ) p(y |x, w ))
q∈Q
= argmax H(q) − µF ,yF (q)EF (yF ; xF , w ) − log Z (x, w )
q∈Q
F ∈F yF ∈YF
= argmax H(q) − µF ,yF (q)EF (yF ; xF , w )
q∈Q
F ∈F yF ∈YF
= argmax − qi (yi ) log qi (yi )
q∈Q
i∈V yi ∈Yi
− qi (yi ) EF (yF ; xF , w ) .
F ∈F yF ∈YF i∈N(F )
Optimizing over Q is optimizing over qi ∈ ∆i , the probability simplices.
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

43. Belief Propagation Variational Inference Sampling Break
Variational Inference
Naive Mean Field (cont)
argmax − qi (yi ) log qi (yi )
q∈Q
i∈V yi ∈Yi
− qi (yi ) EF (yF ; xF , w ) .
F ∈F yF ∈YF i∈N(F )
Non-concave maximization problem →
hard. (For general EF and pairwise or F qf
ˆ
higher-order factors.) µF
Block coordinate ascent: closed-form qi
qh
ˆ qj
ˆ
update for each qi
ql
ˆ
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

44. Belief Propagation Variational Inference Sampling Break
Variational Inference
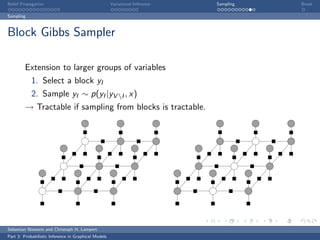
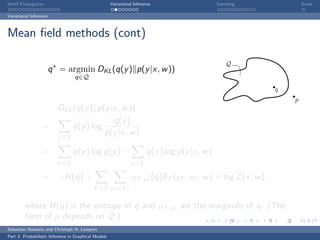
Naive Mean Field (cont)
Closed form update for qi :
 
qi∗ (yi ) =
 
exp 1 −
 qj (yj ) EF (yF ; xF , w ) + λ
ˆ 
F ∈F , yF ∈YF , j∈N(F ){i}
i∈N(F ) [yF ]i =yi
 
 
λ = − log 
 exp 1 − qj (yj ) EF (yF ; xF , w ) 
ˆ 
yi ∈Yi F ∈F , yF ∈YF ,j∈N(F ){i}
i∈N(F ) [yF ]i =yi
Look scary, but very easy to implement
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

45. Belief Propagation Variational Inference Sampling Break
Variational Inference
Structured Mean Field
Naive mean field approximation can be poor
Structured mean field (Saul and Jordan, 1995) uses factorial
approximations with larger tractable subgraphs
Block coordinate ascent: optimizing an entire subgraph using exact
probabilistic inference on trees
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

46. Belief Propagation Variational Inference Sampling Break
Sampling
Sampling
Probabilistic inference and related tasks require the computation of
Ey ∼p(y |x,w ) [h(x, y )],
where h : X × Y → R is an arbitary but well-behaved function.
Inference: hF ,zF (x, y ) = I (yF = zF ),
Ey ∼p(y |x,w ) [hF ,zF (x, y )] = p(yF = zF |x, w ),
the marginal probability of factor F taking state zF .
Parameter estimation: feature map h(x, y ) = φ(x, y ),
φ : X × Y → Rd ,
Ey ∼p(y |x,w ) [φ(x, y )],
“expected sufficient statistics under the model distribution”.
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

47. Belief Propagation Variational Inference Sampling Break
Sampling
Sampling
Probabilistic inference and related tasks require the computation of
Ey ∼p(y |x,w ) [h(x, y )],
where h : X × Y → R is an arbitary but well-behaved function.
Inference: hF ,zF (x, y ) = I (yF = zF ),
Ey ∼p(y |x,w ) [hF ,zF (x, y )] = p(yF = zF |x, w ),
the marginal probability of factor F taking state zF .
Parameter estimation: feature map h(x, y ) = φ(x, y ),
φ : X × Y → Rd ,
Ey ∼p(y |x,w ) [φ(x, y )],
“expected sufficient statistics under the model distribution”.
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

48. Belief Propagation Variational Inference Sampling Break
Sampling
Sampling
Probabilistic inference and related tasks require the computation of
Ey ∼p(y |x,w ) [h(x, y )],
where h : X × Y → R is an arbitary but well-behaved function.
Inference: hF ,zF (x, y ) = I (yF = zF ),
Ey ∼p(y |x,w ) [hF ,zF (x, y )] = p(yF = zF |x, w ),
the marginal probability of factor F taking state zF .
Parameter estimation: feature map h(x, y ) = φ(x, y ),
φ : X × Y → Rd ,
Ey ∼p(y |x,w ) [φ(x, y )],
“expected sufficient statistics under the model distribution”.
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

49. Belief Propagation Variational Inference Sampling Break
Sampling
Monte Carlo
Sample approximation from y (1) , y (2) , . . .
S
1
Ey ∼p(y |x,w ) [h(x, y )] ≈ h(x, y (s) ).
S s=1
When the expectation exists, then the law of large numbers
guarantees convergence for S → ∞,
√
For S independent samples, approximation error is O(1/ S),
independent of the dimension d.
Problem
Producing exact samples y (s) from p(y |x) is hard
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

50. Belief Propagation Variational Inference Sampling Break
Sampling
Monte Carlo
Sample approximation from y (1) , y (2) , . . .
S
1
Ey ∼p(y |x,w ) [h(x, y )] ≈ h(x, y (s) ).
S s=1
When the expectation exists, then the law of large numbers
guarantees convergence for S → ∞,
√
For S independent samples, approximation error is O(1/ S),
independent of the dimension d.
Problem
Producing exact samples y (s) from p(y |x) is hard
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

51. Belief Propagation Variational Inference Sampling Break
Sampling
Markov Chain Monte Carlo (MCMC)
Markov chain with p(y |x) as
stationary distribution 0.5 B
0.1
0.25 0.4
Here: Y = {A, B, C }
Here: p(y ) = (0.1905, 0.3571, 0.4524)
A 0.5 0.5
0.25
C
0.5
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

52. Belief Propagation Variational Inference Sampling Break
Sampling
Markov Chains
Definition (Finite Markov chain)
0.5 B
Given a finite set Y and a matrix 0.1
P ∈ RY×Y , then a random process 0.25 0.4
(Z1 , Z2 , . . . ) with Zt taking values from Y A 0.5 0.5
is a Markov chain with transition matrix P,
if
0.25
p(Zt+1 = y (j) |Z1 = y (1) , Z2 = y (2) , . . . , Zt = y (t) )
C
0.5
= p(Zt+1 = y (j) |Zt = y (t) )
= Py (t) ,y (j)
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

53. Belief Propagation Variational Inference Sampling Break
Sampling
MCMC Simulation (1)
Steps
1. Construct a Markov chain with stationary distribution p(y |x, w )
2. Start at y (0)
3. Perform random walk according to Markov chain
4. After sufficient number S of steps, stop and treat y (S) as sample
from p(y |x, w )
Justified by ergodic theorem.
In practise: discard a fixed number of initial samples (“burn-in
phase”) to forget starting point
In practise: afterwards, use between 100 to 100, 000 samples
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

54. Belief Propagation Variational Inference Sampling Break
Sampling
MCMC Simulation (1)
Steps
1. Construct a Markov chain with stationary distribution p(y |x, w )
2. Start at y (0)
3. Perform random walk according to Markov chain
4. After sufficient number S of steps, stop and treat y (S) as sample
from p(y |x, w )
Justified by ergodic theorem.
In practise: discard a fixed number of initial samples (“burn-in
phase”) to forget starting point
In practise: afterwards, use between 100 to 100, 000 samples
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

55. Belief Propagation Variational Inference Sampling Break
Sampling
MCMC Simulation (1)
Steps
1. Construct a Markov chain with stationary distribution p(y |x, w )
2. Start at y (0)
3. Perform random walk according to Markov chain
4. After each step, output y (i) as sample from p(y |x, w )
Justified by ergodic theorem.
In practise: discard a fixed number of initial samples (“burn-in
phase”) to forget starting point
In practise: afterwards, use between 100 to 100, 000 samples
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

56. Belief Propagation Variational Inference Sampling Break
Sampling
MCMC Simulation (1)
Steps
1. Construct a Markov chain with stationary distribution p(y |x, w )
2. Start at y (0)
3. Perform random walk according to Markov chain
4. After each step, output y (i) as sample from p(y |x, w )
Justified by ergodic theorem.
In practise: discard a fixed number of initial samples (“burn-in
phase”) to forget starting point
In practise: afterwards, use between 100 to 100, 000 samples
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

57. Belief Propagation Variational Inference Sampling Break
Sampling
Gibbs sampler
How to construct a suitable Markov chain?
Metropolis-Hastings chain, almost always possible
Special case: Gibbs sampler (Geman and Geman, 1984)
1. Select a variable yi ,
2. Sample yi ∼ p(yi |yV {i} , x).
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

58. Belief Propagation Variational Inference Sampling Break
Sampling
Gibbs sampler
How to construct a suitable Markov chain?
Metropolis-Hastings chain, almost always possible
Special case: Gibbs sampler (Geman and Geman, 1984)
1. Select a variable yi ,
2. Sample yi ∼ p(yi |yV {i} , x).
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

59. Belief Propagation Variational Inference Sampling Break
Sampling
Gibbs Sampler
(t) (t)
(t)
p(yi , yV {i} |x, w ) p (yi , yV {i} |x, w )
˜
p(yi |yV {i} , x, w ) = (t)
= (t)
yi ∈Yi p(yi , yV {i} |x, w ) yi ∈Yi p (yi , yV {i} |x, w )
˜
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

60. Belief Propagation Variational Inference Sampling Break
Sampling
Gibbs Sampler
(t)
(t) F ∈M(i) exp(−EF (yi , yF {i} , xF , w ))
p(yi |yV {i} , x, w ) = (t)
yi ∈Yi F ∈M(i) exp(−EF (yi , yF {i} , xF , w ))
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

61. Belief Propagation Variational Inference Sampling Break
Sampling
Example: Gibbs sampler
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

62. Belief Propagation Variational Inference Sampling Break
Sampling
Example: Gibbs sampler
Cummulative mean
1
0.95
0.9
0.85
p(foreground)
0.8
0.75
0.7
0.65
0.6
0.55
0.5
0 500 1000 1500 2000 2500 3000
Gibbs sweep
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

63. Belief Propagation Variational Inference Sampling Break
Sampling
Example: Gibbs sampler
Gibbs sample means and average of 50 repetitions
1
0.8
Estimated probability
0.6
0.4
0.2
0
0 500 1000 1500 2000 2500 3000
Gibbs sweep
p(yi = “foreground ) ≈ 0.770 ± 0.011
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

64. Belief Propagation Variational Inference Sampling Break
Sampling
Example: Gibbs sampler
Estimated one unit standard deviation
0.25
0.2
Standard deviation
0.15
0.1
0.05
0
0 500 1000 1500 2000 2500 3000
Gibbs sweep
√
Standard deviation O(1/ S)
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

65. Belief Propagation Variational Inference Sampling Break
Sampling
Gibbs Sampler Transitions
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

66. Belief Propagation Variational Inference Sampling Break
Sampling
Gibbs Sampler Transitions
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

67. Belief Propagation Variational Inference Sampling Break
Sampling
Block Gibbs Sampler
Extension to larger groups of variables
1. Select a block yI
2. Sample yI ∼ p(yI |yV I , x)
→ Tractable if sampling from blocks is tractable.
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

68. Belief Propagation Variational Inference Sampling Break
Sampling
Summary: Sampling
Two families of Monte Carlo methods
1. Markov Chain Monte Carlo (MCMC)
2. Importance Sampling
Properties
Often simple to implement, general, parallelizable
(Cannot compute partition function Z )
Can fail without any warning signs
References
(H¨ggstr¨m, 2000), introduction to Markov chains
a o
(Liu, 2001), excellent Monte Carlo introduction
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models

69. Belief Propagation Variational Inference Sampling Break
Break
Coffee Break
Coffee Break
Continuing at 10:30am
Slides available at
http://www.nowozin.net/sebastian/
cvpr2011tutorial/
Sebastian Nowozin and Christoph H. Lampert
Part 3: Probabilistic Inference in Graphical Models