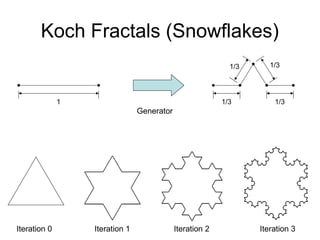
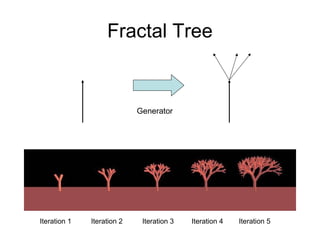
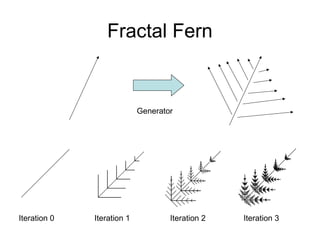
This document discusses fractals and their use in computer graphics. It defines fractals as self-similar geometric objects that can model natural forms. Common fractals include the Koch snowflake and fractal trees & ferns, which are generated through an iterative process. The document also describes how fractals can be used to procedurally generate terrain by applying random mid-point displacement.

1. Fractals
Computer graphics

2. Fractals
• Fractals are geometric objects.
• Many real-world objects like ferns are
shaped like fractals.
• Fractals are formed by iterations.
• Fractals are self-similar.
• In computer graphics, we use fractal
functions to create complex objects.

3. Types of fractals
• Self Similar : These fractals have parts
that are scaled down versions of the entire
object, we construct the object subparts by
applying a scaling parameter s to the
overall shape.
• Self affine : -formed with different scaling
parameters. -terrain,water,clouds are
typically modeled using this.

4. • Invariant Fractal Sets:
this class of fractals includes self squaring
fractals.

5. Koch Fractals (Snowflakes)
1/3
1
1/3
1/3
1/3
Generator
Iteration 0
Iteration 1
Iteration 2
Iteration 3

6. Fractal Tree
Generator
Iteration 1
Iteration 2
Iteration 3
Iteration 4
Iteration 5

7. Fractal Fern
Generator
Iteration 0
Iteration 1
Iteration 2
Iteration 3

8. Add Some Randomness
• The fractals we’ve produced so far seem to be
very regular and “artificial”.
• To create some realism and variability, simply
change the angles slightly sometimes based on
a random number generator.
• For example, you can curve some of the ferns to
one side.
• For example, you can also vary the lengths of
the branches and the branching factor.

9. Terrain (Random Mid-point
Displacement)
• Given the heights of two end-points, generate a
height at the mid-point.
• Suppose that the two end-points are a and b.
Suppose the height is in the y direction, such
that the height at a is y(a), and the height at b is
y(b).
• Then, the height at the mid-point will be:
ymid = (y(a)+y(b))/2 + r, where
– r is the random offset
• This is how to generate the random offset r:
r = srg|b-a|, where
– s is a user-selected “roughness” factor, and
– rg is a Gaussian random variable with mean 0 and variance 1

10. How to generate a random number with
Gaussian (or normal) probability distribution
// given random numbers x1 and x2 with equal distribution from -1 to 1
// generate numbers y1 and y2 with normal distribution centered at 0.0
// and with standard deviation 1.0.
void Gaussian(float &y1, float &y2) {
float x1, x2, w;
do {
x1 = 2.0 * 0.001*(float)(rand()%1000) - 1.0;
x2 = 2.0 * 0.001*(float)(rand()%1000) - 1.0;
w = x1 * x1 + x2 * x2;
} while ( w >= 1.0 );
w = sqrt( (-2.0 * log( w ) ) / w );
y1 = x1 * w;
y2 = x2 * w;
}

11. Procedural Terrain Example

12. Building a more realistic terrain
• Notice that in the real world, valleys and
mountains have different shapes.
• If we have the same terrain-generation algorithm
for both mountains and valleys, it will result in
unrealistic, alien-looking landscapes.
• Therefore, use different parameters for valleys
and mountains.
• Also, can manually create ridges, cliffs, and
other geographical features, and then use
fractals to create detail roughness.