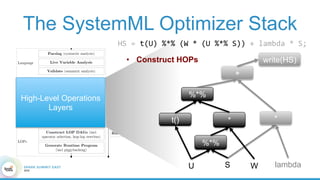
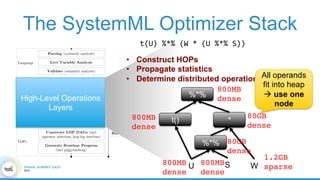
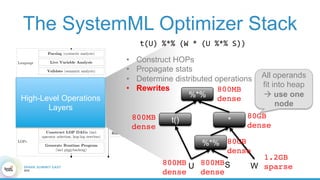
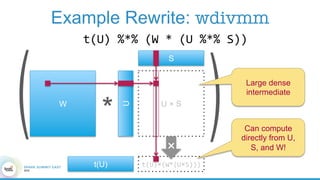
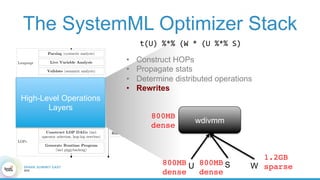
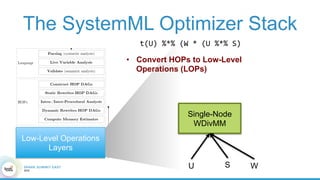
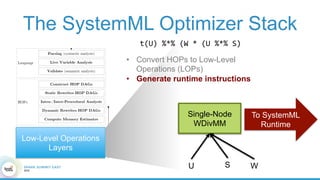
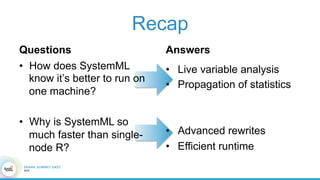
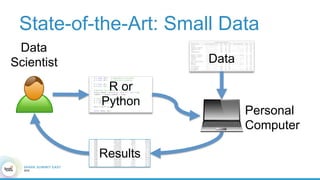
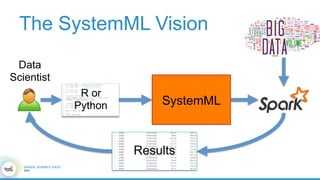
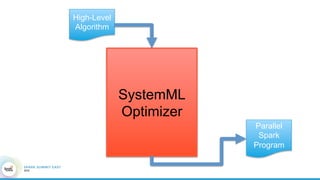
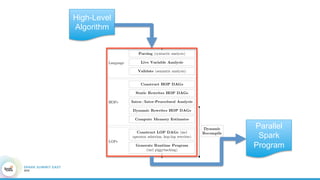
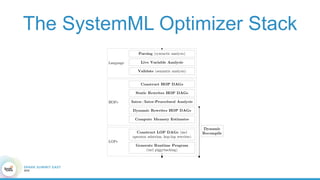
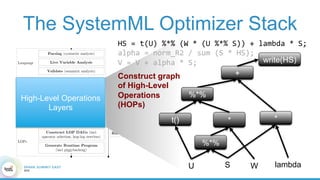
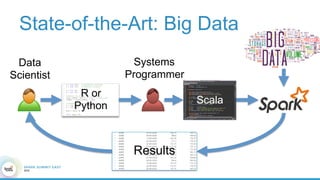
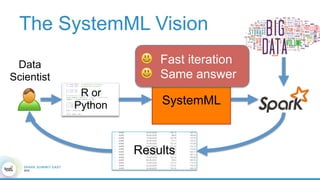
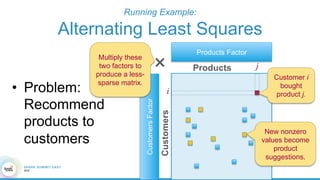
1. The document describes the origins and goals of the SystemML project for scalable machine learning. 2. SystemML was created to allow data scientists to write machine learning algorithms in R and automatically compile and optimize them to run efficiently on large datasets in parallel. 3. An example alternating least squares algorithm is shown written concisely in R, while traditional approaches required translating algorithms to other languages like Scala which was error-prone and slowed iteration. SystemML aims to allow the same algorithm to run fast at large scale with the same answer.

1. Inside Apache SystemML
Fred Reiss
Chief Architect, IBM Spark Technology Center
Member of the IBM Academy of Technology

2. • 2007-2008: Multiple projects at IBM Research –
Almaden involving machine learning on Hadoop.
• 2009: We create a dedicated team for scalable ML.
• 2009-2010: Through engagements with customers, we
observe how data scientists create machine learning
algorithms.
Origins of the SystemML Project

3. State-of-the-Art: Small Data
R or
Python
Data
Scientist
Personal
Computer
Data
Results

4. State-of-the-Art: Big Data
R or
Python
Data
Scientist
Results
Systems
Programmer
Scala

5. State-of-the-Art: Big Data
R or
Python
Data
Scientist
Results
Systems
Programmer
Scala
😞 Days or weeks per iteration
😞 Errors while translating
algorithms

6. The SystemML Vision
R or
Python
Data
Scientist
Results
SystemML

7. The SystemML Vision
R or
Python
Data
Scientist
Results
SystemML
😃 Fast iteration
😃 Same answer

8. Running Example:
Alternating Least Squares
Products
Customers
i
j
Customer i
bought
product j.
Products Factor
CustomersFactor
Multiply these
two factors to
produce a less-
sparse matrix.
×
New nonzero
values become
product
suggestions.
• Problem:
Recommend
products to
customers

9. Alternating Least Squares (in R)
U = rand(nrow(X), r, min = -1.0, max = 1.0);
V = rand(r, ncol(X), min = -1.0, max = 1.0);
while(i < mi) {
i = i + 1; ii = 1;
if (is_U)
G = (W * (U %*% V - X)) %*% t(V) + lambda * U;
else
G = t(U) %*% (W * (U %*% V - X)) + lambda * V;
norm_G2 = sum(G ^ 2); norm_R2 = norm_G2;
R = -G; S = R;
while(norm_R2 > 10E-9 * norm_G2 & ii <= mii) {
if (is_U) {
HS = (W * (S %*% V)) %*% t(V) + lambda * S;
alpha = norm_R2 / sum (S * HS);
U = U + alpha * S;
} else {
HS = t(U) %*% (W * (U %*% S)) + lambda * S;
alpha = norm_R2 / sum (S * HS);
V = V + alpha * S;
}
R = R - alpha * HS;
old_norm_R2 = norm_R2; norm_R2 = sum(R ^ 2);
S = R + (norm_R2 / old_norm_R2) * S;
ii = ii + 1;
}
is_U = ! is_U;
}

10. Alternating Least Squares (in R)
U = rand(nrow(X), r, min = -1.0, max = 1.0);
V = rand(r, ncol(X), min = -1.0, max = 1.0);
while(i < mi) {
i = i + 1; ii = 1;
if (is_U)
G = (W * (U %*% V - X)) %*% t(V) + lambda * U;
else
G = t(U) %*% (W * (U %*% V - X)) + lambda * V;
norm_G2 = sum(G ^ 2); norm_R2 = norm_G2;
R = -G; S = R;
while(norm_R2 > 10E-9 * norm_G2 & ii <= mii) {
if (is_U) {
HS = (W * (S %*% V)) %*% t(V) + lambda * S;
alpha = norm_R2 / sum (S * HS);
U = U + alpha * S;
} else {
HS = t(U) %*% (W * (U %*% S)) + lambda * S;
alpha = norm_R2 / sum (S * HS);
V = V + alpha * S;
}
R = R - alpha * HS;
old_norm_R2 = norm_R2; norm_R2 = sum(R ^ 2);
S = R + (norm_R2 / old_norm_R2) * S;
ii = ii + 1;
}
is_U = ! is_U;
}
1. Start with random factors.
2. Hold the Products factor constant
and find the best value for the
Customers factor.
(Value that most closely approximates the original
matrix)
3. Hold the Customers factor
constant and find the best value
for the Products factor.
4. Repeat steps 2-3 until
convergence.
1
2
2
3
3
4
4
4
Every line has a clear purpose!

11. Alternating Least Squares (spark.ml)

12. Alternating Least Squares (spark.ml)

13. Alternating Least Squares (spark.ml)

14. Alternating Least Squares (spark.ml)

15. • 25 lines’ worth of algorithm…
• …mixed with 800 lines of performance code

16. Alternating Least Squares (in R)
U = rand(nrow(X), r, min = -1.0, max = 1.0);
V = rand(r, ncol(X), min = -1.0, max = 1.0);
while(i < mi) {
i = i + 1; ii = 1;
if (is_U)
G = (W * (U %*% V - X)) %*% t(V) + lambda * U;
else
G = t(U) %*% (W * (U %*% V - X)) + lambda * V;
norm_G2 = sum(G ^ 2); norm_R2 = norm_G2;
R = -G; S = R;
while(norm_R2 > 10E-9 * norm_G2 & ii <= mii) {
if (is_U) {
HS = (W * (S %*% V)) %*% t(V) + lambda * S;
alpha = norm_R2 / sum (S * HS);
U = U + alpha * S;
} else {
HS = t(U) %*% (W * (U %*% S)) + lambda * S;
alpha = norm_R2 / sum (S * HS);
V = V + alpha * S;
}
R = R - alpha * HS;
old_norm_R2 = norm_R2; norm_R2 = sum(R ^ 2);
S = R + (norm_R2 / old_norm_R2) * S;
ii = ii + 1;
}
is_U = ! is_U;
}

17. Alternating Least Squares (in R)
U = rand(nrow(X), r, min = -1.0, max = 1.0);
V = rand(r, ncol(X), min = -1.0, max = 1.0);
while(i < mi) {
i = i + 1; ii = 1;
if (is_U)
G = (W * (U %*% V - X)) %*% t(V) + lambda * U;
else
G = t(U) %*% (W * (U %*% V - X)) + lambda * V;
norm_G2 = sum(G ^ 2); norm_R2 = norm_G2;
R = -G; S = R;
while(norm_R2 > 10E-9 * norm_G2 & ii <= mii) {
if (is_U) {
HS = (W * (S %*% V)) %*% t(V) + lambda * S;
alpha = norm_R2 / sum (S * HS);
U = U + alpha * S;
} else {
HS = t(U) %*% (W * (U %*% S)) + lambda * S;
alpha = norm_R2 / sum (S * HS);
V = V + alpha * S;
}
R = R - alpha * HS;
old_norm_R2 = norm_R2; norm_R2 = sum(R ^ 2);
S = R + (norm_R2 / old_norm_R2) * S;
ii = ii + 1;
}
is_U = ! is_U;
}
(in SystemML’s
subset of R)
• SystemML can
compile and run this
algorithm at scale
• No additional
performance code
needed!

18. How fast does it run?
Running time comparisons between
machine learning algorithms are
problematic
– Different, equally-valid answers
– Different convergence rates on different
data
– But we’ll do one anyway

19. Performance Comparison: ALS
0
5000
10000
15000
20000
1.2GB (sparse
binary)
12GB 120GB
RunningTime(sec)
R
MLLib
SystemML
>24h>24h
OOM
OOM
Synthetic data, 0.01 sparsity, 10^5 products × {10^5,10^6,10^7} users. Data generated by multiplying two rank-50 matrices of normally-distributed
data, sampling from the resulting product, then adding Gaussian noise. Cluster of 6 servers with 12 cores and 96GB of memory per server.
Number of iterations tuned so that all algorithms produce comparable result quality.Details:

20. Takeaway Points
• SystemML runs the R script in parallel
– Same answer as original R script
– Performance is comparable to a low-level
RDD-based implementation
• How does SystemML achieve this result?

21. Performance Comparison: ALS
0
5000
10000
15000
20000
1.2GB (sparse
binary)
12GB 120GB
RunningTime(sec)
R
MLLib
SystemML
>24h>24h
OOM
OOM
Synthetic data, 0.01 sparsity, 10^5 products × {10^5,10^6,10^7} users. Data generated by multiplying two rank-50 matrices of normally-distributed
data, sampling from the resulting product, then adding Gaussian noise. Cluster of 6 servers with 12 cores and 96GB of memory per server.
Number of iterations tuned so that all algorithms produce comparable result quality.Details:
Several factors at play
• Subtly different
algorithms
• Adaptive execution
strategies
• Runtime differences
Several factors at play
• Subtly different
algorithms
• Adaptive execution
strategies
• Runtime differences

22. Questions We’ll Focus On
0
5000
10000
15000
20000
1.2GB (sparse
binary)
12GB 120GB
RunningTime(sec)
R
MLLib
SystemML
>24h>24h
OOM
OOM
SystemML runs no
distributed jobs here.
• How does SystemML
know it’s better to run on
one machine?
• Why is SystemML so
much faster than single-
node R?

23. Questions We’ll Focus On
0
5000
10000
15000
20000
1.2GB (sparse
binary)
12GB 120GB
RunningTime(sec)
R
MLLib
SystemML
>24h>24h
OOM
OOM
SystemML runs no
distributed jobs here.
• How does SystemML
know it’s better to run
on one machine?
• Why is SystemML so
much faster than single-
node R?

24. SystemML
Optimizer
High-Level
Algorithm
Parallel
Spark
Program

25. High-Level
Algorithm
Parallel
Spark
Program

26. The SystemML Optimizer Stack

27. The SystemML Optimizer Stack

28. The SystemML Optimizer Stack
Abstract Syntax Tree
Layers
U = rand(nrow(X), r, min = -1.0, max = 1.0);
V = rand(r, ncol(X), min = -1.0, max = 1.0);
while(i < mi) {
i = i + 1; ii = 1;
if (is_U)
G = (W * (U %*% V - X)) %*% t(V) + lambda * U;
else
G = t(U) %*% (W * (U %*% V - X)) + lambda * V;
norm_G2 = sum(G ^ 2); norm_R2 = norm_G2;
R = -G; S = R;
while(norm_R2 > 10E-9 * norm_G2 & ii <= mii) {
if (is_U) {
HS = (W * (S %*% V)) %*% t(V) + lambda * S;
alpha = norm_R2 / sum (S * HS);
U = U + alpha * S;
} else {
HS = t(U) %*% (W * (U %*% S)) + lambda * S;
alpha = norm_R2 / sum (S * HS);
V = V + alpha * S;
}
R = R - alpha * HS;
old_norm_R2 = norm_R2; norm_R2 = sum(R ^ 2);
S = R + (norm_R2 / old_norm_R2) * S;
ii = ii + 1;
}
is_U = ! is_U;
}
• Parsing
• Live variable
analysis
• Validation

29. The SystemML Optimizer Stack
Abstract Syntax Tree
Layers
U = rand(nrow(X), r, min = -1.0, max = 1.0);
V = rand(r, ncol(X), min = -1.0, max = 1.0);
while(i < mi) {
i = i + 1; ii = 1;
if (is_U)
G = (W * (U %*% V - X)) %*% t(V) + lambda * U;
else
G = t(U) %*% (W * (U %*% V - X)) + lambda * V;
norm_G2 = sum(G ^ 2); norm_R2 = norm_G2;
R = -G; S = R;
while(norm_R2 > 10E-9 * norm_G2 & ii <= mii) {
if (is_U) {
HS = (W * (S %*% V)) %*% t(V) + lambda * S;
alpha = norm_R2 / sum (S * HS);
U = U + alpha * S;
} else {
HS = t(U) %*% (W * (U %*% S)) + lambda * S;
alpha = norm_R2 / sum (S * HS);
V = V + alpha * S;
}
R = R - alpha * HS;
old_norm_R2 = norm_R2; norm_R2 = sum(R ^ 2);
S = R + (norm_R2 / old_norm_R2) * S;
ii = ii + 1;
}
is_U = ! is_U;
}
• Parsing
• Live variable
analysis
• Validation

30. +
The SystemML Optimizer Stack
High-Level Operations
Layers
HS = t(U) %*% (W * (U %*% S)) + lambda * S;
alpha = norm_R2 / sum (S * HS);
V = V + alpha * S;
%*%
WU S
*t()
lambda
*
%*%
write(HS)
Construct graph
of High-Level
Operations
(HOPs)

31. +
The SystemML Optimizer Stack
High-Level Operations
Layers
HS = t(U) %*% (W * (U %*% S)) + lambda * S;
%*%
WU S
*t()
lambda
*
%*%
write(HS)• Construct HOPs

32. The SystemML Optimizer Stack
High-Level Operations
Layers
HS = t(U) %*% (W * (U %*% S))
%*%
WU S
*t()
%*%
1.2GB
sparse
80GB
dense
80GB
dense
800MB
dense
800MB
dense
800MB
dense
• Construct HOPs
• Propagate statistics
• Determine distributed operationsAll operands
fit into heap
à use one
node
800MB
dense

33. Questions We’ll Focus On
0
5000
10000
15000
20000
1.2GB (sparse
binary)
12GB 120GB
RunningTime(sec)
R
MLLib
SystemML
>24h>24h
OOM
OOM
SystemML runs no
distributed jobs here.
• How does SystemML
know it’s better to run on
one machine?
• Why is SystemML so
much faster than
single-node R?

34. The SystemML Optimizer Stack
High-Level Operations
Layers
HS = t(U) %*% (W * (U %*% S))
%*%
WU S
*t()
%*%
1.2GB
sparse
80GB
dense
80GB
dense
800MB
dense
800MB
dense
800MB
dense
All operands
fit into heap
à use one
node
• Construct HOPs
• Propagate stats
• Determine distributed operations
• Rewrites
800MB
dense

35. Example Rewrite: wdivmm
W
S
U
U × S
*( (
t(U) t(U)×(W*(U×S)))
×
Large dense
intermediate
Can compute
directly from U,
S, and W!
t(U) %*% (W * (U %*% S))

36. The SystemML Optimizer Stack
High-Level Operations
Layers
HS = t(U) %*% (W * (U %*% S)
wdivmm
WU S
1.2GB
sparse
800MB
dense
800MB
dense
• Construct HOPs
• Propagate stats
• Determine distributed operations
• Rewrites
800MB
dense

37. The SystemML Optimizer Stack
Low-Level Operations
Layers
HS = t(U) %*% (W * (U %*% S)
wdivmm
WU S
1.2GB
sparse
800MB
dense
800MB
dense
800MB
dense
• Convert HOPs to Low-Level
Operations (LOPs)

38. The SystemML Optimizer Stack
Low-Level Operations
Layers
HS = t(U) %*% (W * (U %*% S)
Single-Node
WDivMM
WU S
• Convert HOPs to Low-Level
Operations (LOPs)

39. The SystemML Optimizer Stack
Low-Level Operations
Layers
HS = t(U) %*% (W * (U %*% S)
Single-Node
WDivMM
WU S
• Convert HOPs to Low-Level
Operations (LOPs)
• Generate runtime instructions
To SystemML
Runtime

40. The SystemML Runtime for Spark
• Automates critical performance decisions
– Distributed or local computation?
– How to partition the data?
– To persist or not to persist?

41. The SystemML Runtime for Spark
• Distributed vs local: Hybrid runtime
– Multithreaded computation in Spark Driver
– Distributed computation in Spark Executors
– Optimizer makes a cost-based choice

42. The SystemML Runtime for Spark
Efficient Linear Algebra
• Binary block matrices
(JavaPairRDD<MatrixIndexes, MatrixBlock>)
• Adaptive block storage formats: Dense, Sparse,
Ultra-Sparse, Empty
• Efficient kernels for all combinations of block
types
Automated RDD
Caching
• Lineage tracking for RDDs/
broadcasts
• Guarded RDD collect/parallelize
• Partitioned Broadcast variables
Logical Blocking
(w/ Bc=1,000)
Physical Blocking and Partitioning
(w/ Bc=1,000)

43. Recap
Questions
• How does SystemML
know it’s better to run on
one machine?
• Why is SystemML so
much faster than single-
node R?
Answers
• Live variable analysis
• Propagation of statistics
• Advanced rewrites
• Efficient runtime

44. But wait, there’s more!
• Many other rewrites
• Cost-based selection of physical operators
• Dynamic recompilation for accurate stats
• Parallel FOR (ParFor) optimizer
• Direct operations on RDD partitions
• YARN and MapReduce support

45. • SystemML is open source!
– Announced in June 2015
– Available on Github since September 1
– First open-source binary release (0.8.0) in October 2015
– Entered Apache incubation in November 2015
– First Apache open-source binary release (0.9) available now
• We are actively seeking contributors and users!
http://systemml.apache.org/
Open-Sourcing SystemML

46. THANK YOU.
For more information, go to
http://systemml.apache.org/