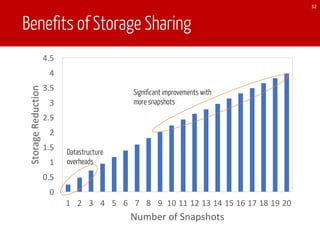
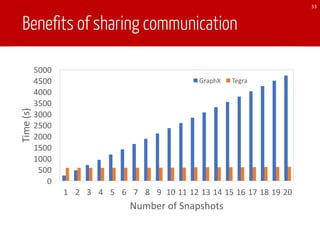
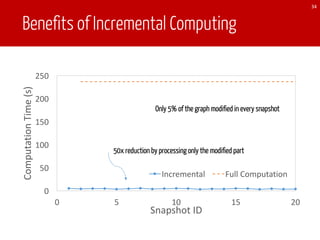
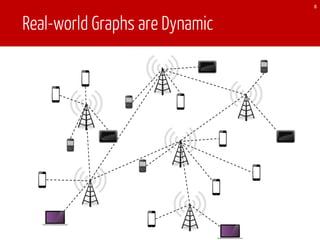
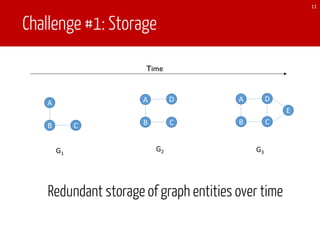
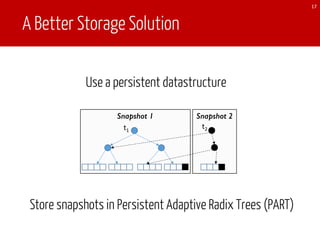
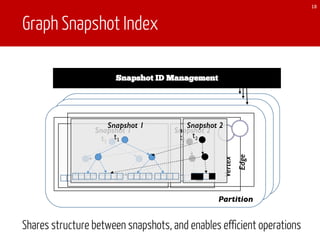
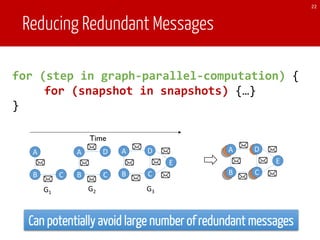
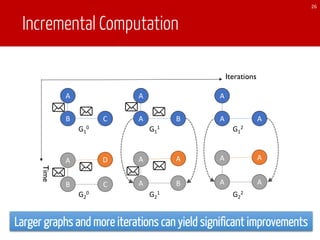
The document discusses TEgra, a framework designed for efficient processing of time-evolving graphs on commodity clusters, addressing challenges in storage, computation, and communication. It highlights the sharing of storage and computation as key strategies for optimizing performance, and presents enhancements to the GraphX API for handling dynamic graphs. The research indicates significant improvements in efficiency through incremental computation and storage sharing based on real-world graph evaluations.

1. Tegra
Time-evolving Graph Processing on
Commodity Clusters
Anand Iyer Joseph GonzalezQifan Pu Ion Stoica
Spark Summit East
8 February 2017

2. About Me
1
• PhD Candidate at AMP/RISE Lab at UC Berkeley
• Thesis on time-evolving graph processing
• Previous work:
• Collaborative energy diagnosis for smartphones
(carat.cs.berkeley.edu)
• Approximate query processing (BlinkDB)
• Cellular Network Analytics
• Fundamental trade-offs in applying ML to real-time datasets

3. Graphs are everywhere…
Social Networks
2

4. Graphs are everywhere…
Gnutella network subgraph
3

5. Graphs are everywhere…
4

6. Graphs are everywhere…
Metabolic network of a single cell organism Tuberculosis
5

7. Plenty of interest in processing them
• Graph DBMS 25% of all enterprises by end of 20171
• Many open-source and research prototypes on distributed graph
processing frameworks: Giraph, Pregel, GraphLab, GraphX, …
1Forrester Research
6

8. Real-world Graphs are Dynamic
Earthquake Occurrence Density
7

9. Real-world Graphs are Dynamic
8

10. Real-world Graphs are Dynamic
9

11. Processing Time-evolving Graphs
Many interesting business and research insights
possible by processing such dynamic graphs…
10
… little or no work in supporting such workloads in
existing graph-processing frameworks

12. Challenge #1: Storage
11
Time
A
B C
G1
A
B C
D
G2
Redundant storage of graph entities over time
A
B C
D
E
G3

13. Challenge #2: Computation
12
A
B C
R1
A
B C
D
E
R3
Wasted computation across snapshots
Time
A
B C
G1
A
B C
D
G2
A
B C
D
E
G3
A
B C
D
R2

14. Challenge #3: Communication
13
A
B C
A
B C
D A
B C
D
E
Time
A
B C
G1
A
B C
D
G2
A
B C
D
E
G3
Duplicate messages sent over the network

15. How do we process time-evolving,
dynamically changing graphs
efficiently?
14
Share
Storage
Communication
Computation
Tegra

16. How do we process time-evolving,
dynamically changing graphs
efficiently?
15
Share
Storage
Communication
Computation
Tegra

17. Sharing Storage
16
Time
A
B C
G1
A
B C
δg1
A D
δg2
A
B C
D
G2
A
B C
D
E
G3
C
D
E
δg3
Storing deltas result in the most optimal storage, but creating
snapshot from deltas can be expensive!

18. A Better Storage Solution
17
Snapshot 2Snapshot 1
t1
t2
Use a persistent datastructure
Store snapshots in Persistent Adaptive Radix Trees (PART)

19. Graph Snapshot Index
18
Snapshot 2Snapshot 1
Vertex
t1
t2
Snapshot 2Snapshot 1
t1
t2
Edge
Partition
Snapshot ID Management
Shares structure between snapshots, and enables efficient operations

20. How do we process time-evolving,
dynamically changing graphs
efficiently?
19
Share
Storage
Communication
Computation
Tegra

21. Graph Parallel Abstraction - GAS
Gather: Accumulate information from neighborhood
20
Apply: Apply the accumulated value
Scatter: Update adjacent edges & vertices with updated value

22. Processing Multiple Snapshots
21
for (snapshot in snapshots) {
for (stage in graph-parallel-computation) {…}
}
A
B C
A
B C
D A
B C
D
E
Time
G1 G2
G3

23. Reducing Redundant Messages
22
A
B C
A
B C
D A
B C
D
E
Time
G1
G2 G3
D
BCBA
AAA
B C
D
E
for (step in graph-parallel-computation) {
for (snapshot in snapshots) {…}
}
Can potentially avoid large number of redundant messages

24. How do we process time-evolving,
dynamically changing graphs
efficiently?
23
Share
Storage
Communication
Computation
Tegra

25. Updating Results
• If result from a previous snapshot is available, how can we reuse
them?
• Three approaches in the past:
• Restart the algorithm
• Redundant computations
• Memoization (GraphInc1)
• Too much state
• Operator-wise state (Naiad2,3)
• Too much overhead
• Fault tolerance
24
1Facilitating real- time graph mining, CloudDB ’12
2 Naiad: A timely dataflow system, SOSP ’13
3 Differential dataflow, CIDR ‘13

26. Key Idea
• Leverage how GAS model executes computation
• Each iteration in GAS modifies the graph by a little
• Can be seen as another time-evolving graph!
• Upon change to a graph:
• Mark parts of the graph that changed
• Expand the marked parts to involve regions for recomputation in every
iteration
• Borrow results from parts not changed
25

27. Incremental Computation
26
A
B C
D
Iterations
Time
A
A B
A A
A A
A
G1
0 G1
1 G1
2
G2
2
A
B C
A
A B
A
A A
G2
0 G2
1
Larger graphs and more iterations can yield significant improvements

28. API
val v = sqlContext.createDataFrame(List(
("a", "Alice"),
("b", "Bob"),
("c", "Charlie")
)).toDF("id", "name")
val e = sqlContext.createDataFrame(List(
("a", "b", "friend"),
("b", "c", "follow"),
("c", "b", "follow)
)).toDF("src", "dst", "relationship")
val g = GraphFrame(v, e)
27
val g1 = g.update(v1, e1)
.indexed()
.indexed()

29. API: Incremental Computations
val g = GraphFrame(v, e)
28
val g1 = g.update(v1,e1)
val result1 = g1.triangleCount.run(result)
val result = g.triangleCount.run()

30. API: Computations on Multiple Graphs
val g = GraphFrame(v, e)
val g1 = g.update(v1,e1)
29
val g2 = g1.update(v2,e2)
val g3 = g1.update(v3,e3)
val results =
g3.triangleCount.runOnSnapshots(start, end)

31. API
30
B C
A D
F E
A DD
B C
D
E
AA
F
Transition
After 11 iteration on graph 2,
Both converge to 3-digit precision
1.224
0.8490.502
2.07
0.8490.502
he benefit of PSR computation.
For each iteration of Pregel,
y of a new graph. When it
ations on the current graph,
he new graph after copying
The new computation will
w active set continue message
s a function of the old active
n the new graph and the old
lgorithms (e.g. incremental
ve set includes vertices from
w vertices and vertices with
class Graph[V, E] {
// Collection views
def vertices(sid: Int): Collection[(Id, V)]
def edges(sid: Int): Collection[(Id, Id, E)]
def triplets(sid: Int): Collection[Triplet]
// Graph-parallel computation
def mrTriplets(f: (Triplet) => M,
sum: (M, M) => M,
sids: Array[Int]): Collection[(Int, Id, M)]
// Convenience functions
def mapV(f: (Id, V) => V,
sids: Array[Int]): Graph[V, E]
def mapE(f: (Id, Id, E) => E
sids: Array[Int]): Graph[V, E]
def leftJoinV(v: Collection[(Id, V)],
f: (Id, V, V) => V,
sids: Array[Int]): Graph[V, E]
def leftJoinE(e: Collection[(Id, Id, E)],
f: (Id, Id, E, E) => E,
sids: Array[Int]): Graph[V, E]
def subgraph(vPred: (Id, V) => Boolean,
ePred: (Triplet) => Boolean,
sids: Array[Int]): Graph[V, E]
def reverse(sids: Array[Int]): Graph[V, E]
}
Listing 3: GraphX [24] operators modified to support Tegra’s

32. Implementation & Evaluation
• Implemented on Spark 2.0
• Extended dataframes with versioning information and iterate
operator
• Extended GraphX API to allow computation on multiple
snapshots
• Preliminary evaluation on two real-world graphs
• Twitter: 41,652,230 vertices, 1,468,365,182 edges
• uk-2007: 105,896,555 vertices, 3,738,733,648 edges
31

33. 0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Storage Reduction
Number of Snapshots
Benefits of Storage Sharing
32
Datastructure
overheads
Significant improvements with
more snapshots

34. Benefits of sharing communication
33
0
500
1000
1500
2000
2500
3000
3500
4000
4500
5000
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Time (s)
Number of Snapshots
GraphX Tegra

35. Benefits of Incremental Computing
34
0
50
100
150
200
250
0 5 10 15 20
Computation Time (s)
Snapshot ID
Incremental Full Computation
Only 5% of the graph modified in every snapshot
50x reduction by processing only the modified part

36. Ongoing/Future Work
• Tight(er) integration with Catalyst
• Tungsten improvements
• Code release
• Incremental pattern matching
• Approximate graph analytics
• Geo-distributed graph analytics
35

37. Summary
• Processing time-evolving graph efficiently can be useful
• Sharing storage, computation and communication key to efficient
time-evolving graph analysis
• We proposed Tegra that implements our ideas
Please talk to us about your interesting use-cases!
api@cs.berkeley.edu
www.cs.berkeley.edu/~api
36