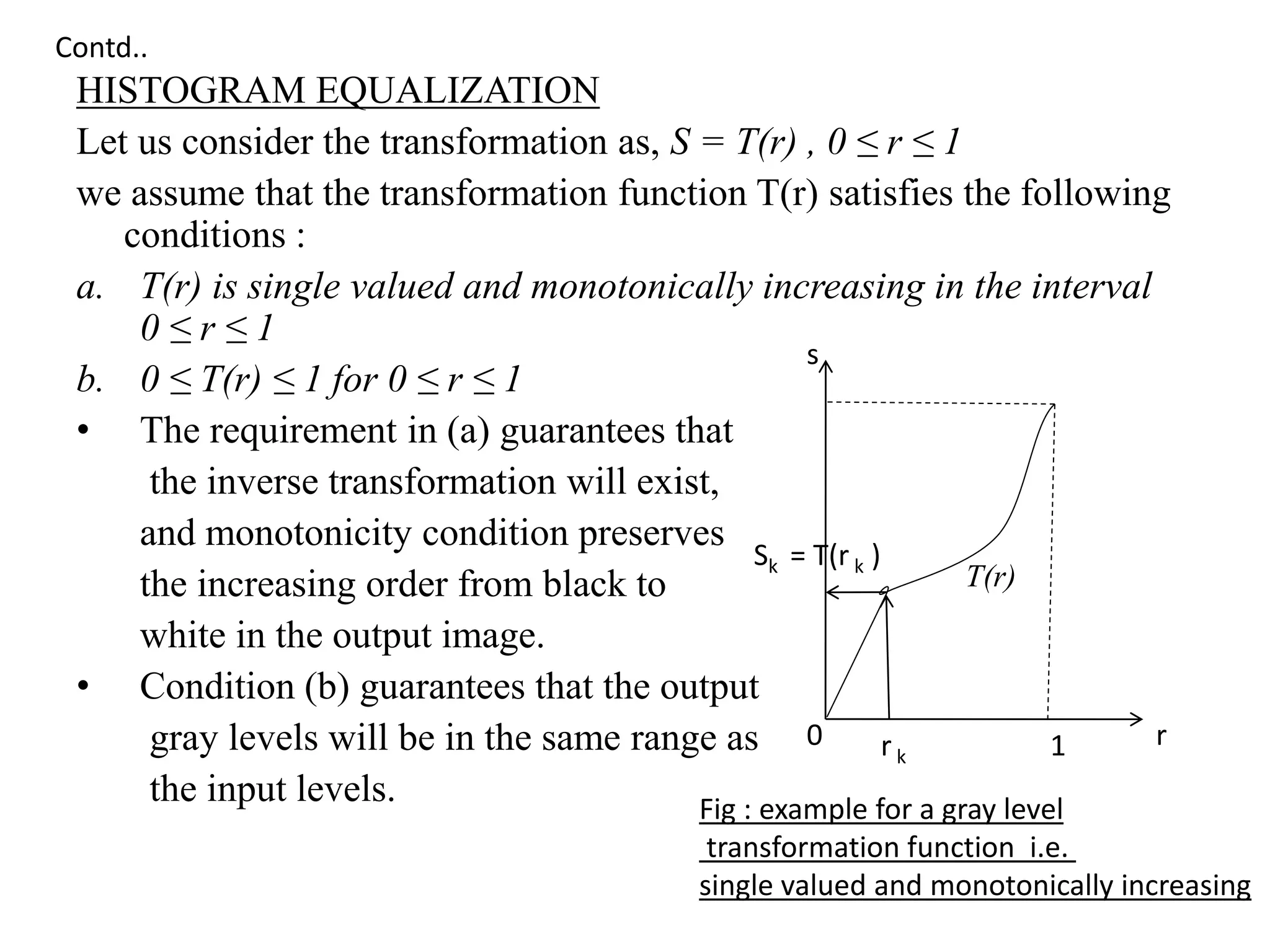
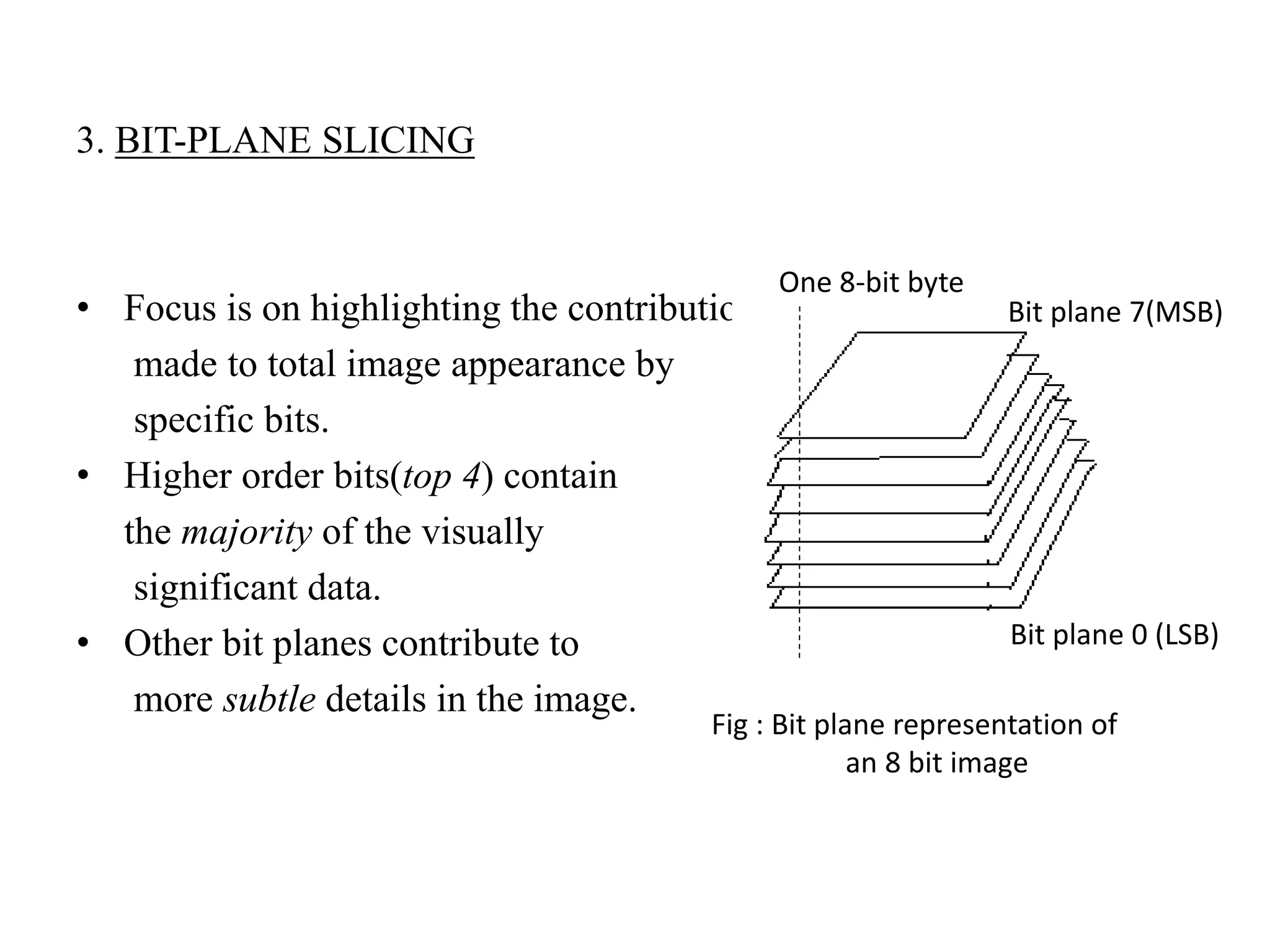
The document discusses various image enhancement techniques, focusing on gray level transformations, histogram processing, and spatial filtering methods. It categorizes enhancement approaches into spatial and frequency domain methods, detailing operations like image negatives, log transformations, and histogram equalization. Additionally, the document outlines the processes of local enhancement and image averaging, emphasizing the importance of manipulating pixel values for better visual representation in specific applications.

2. CONTENTS
• INTRODUCTION
• BACKGROUND
• BASIC GRAY LEVEL TRANSFORMATIONS
• HISTOGRAM PROCESSING
• ENHANCEMENT USING ARITHMETIC/LOGIC OPERATIONS
• BASICS OF SPATIAL FILTERING
• LOCAL ENHANCEMENT

3. INTRODUCTION
• PRINCIPAL OBJECTIVE OF ENHANCEMENT : Process an
image so that the result is more suitable than the original image for
a specific application.
• IMAGE ENHANCEMENT APPROACHES FALL INTO TWO
BROAD CATEGORIES :
1. Spatial Domain Methods
2. Frequency Domain Methods
• Spatial domain refers to the image plane itself and are based on
direct manipulation of pixels in an image.
• Frequency domain processing techniques are based on modifying
the Fourier transform of an image.
• Image enhancement techniques are based on gray level
transformation functions.

4. BACKGROUND
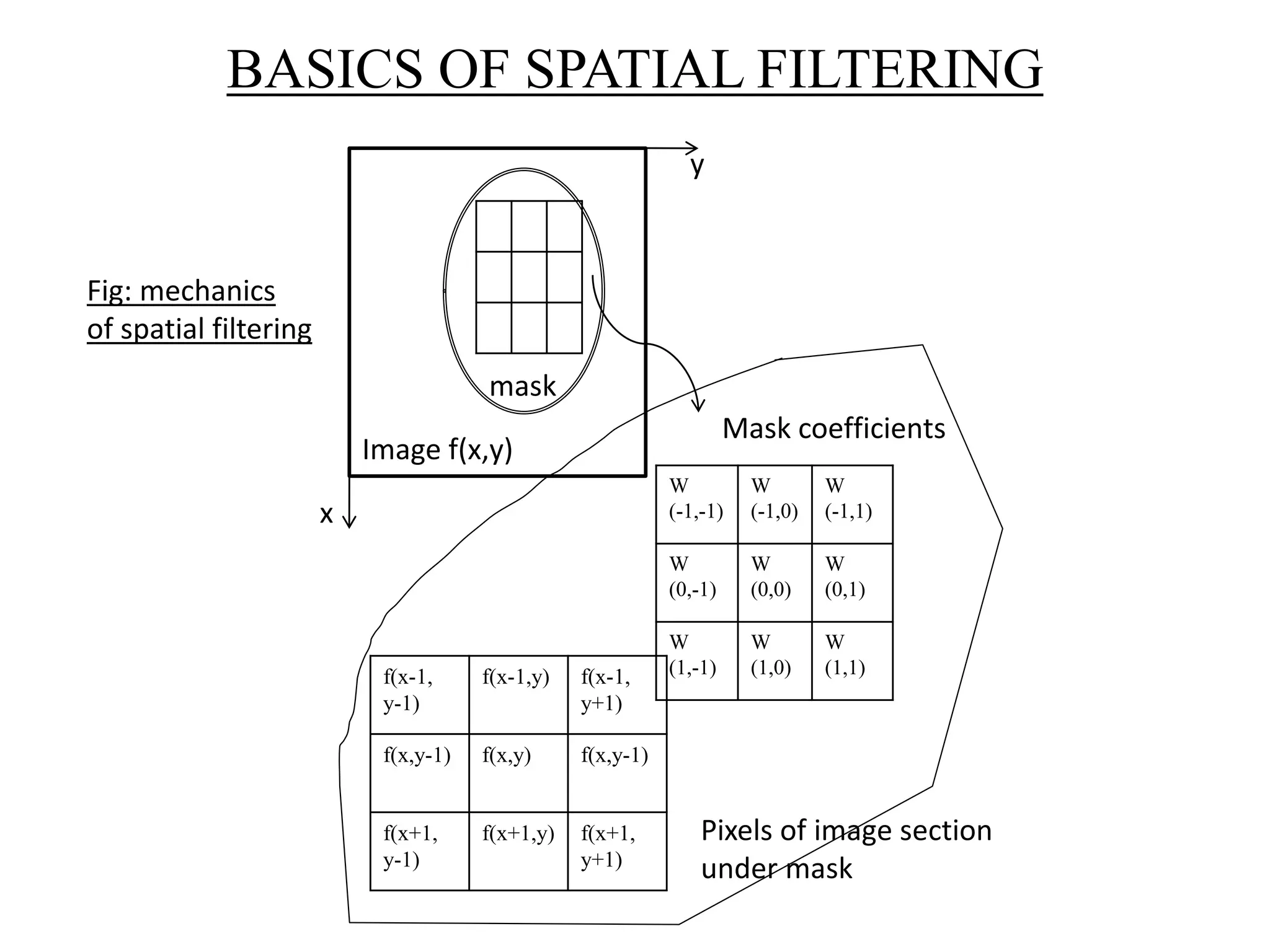
• Spatial domain processes are denoted by the expression
g(x,y) = T[f(x,y)]
where, f(x,y) is input image and g(x,y) is processed image,
T is an operator on f, defined over some neighborhood of (x,y)
• Square or Rectangular subimage area centered
at (x,y) is used as neighborhood
about a point (x,y).
• Here,
T is a gray level transformation function of the
form : s = T(r)
where, r and s – denote the gray levels of f(x,y)
and g(x,y) at any point (x,y). (x,y)
y
x
origin
Fig: 3 x 3 neighborhood about a point (x,y) in an image

5. dark----lightdark----light
dark----light
dark----light
s =T(r)s =T(r)
T(r)
m
rr
Contrast stretching Thresholding function
Fig : Gray level transformation functions for contrast enhancement
• A pixel value of ‘r’ is mapped into a pixel value ‘s’ based
on type of transformation ‘T’
T(r)
m

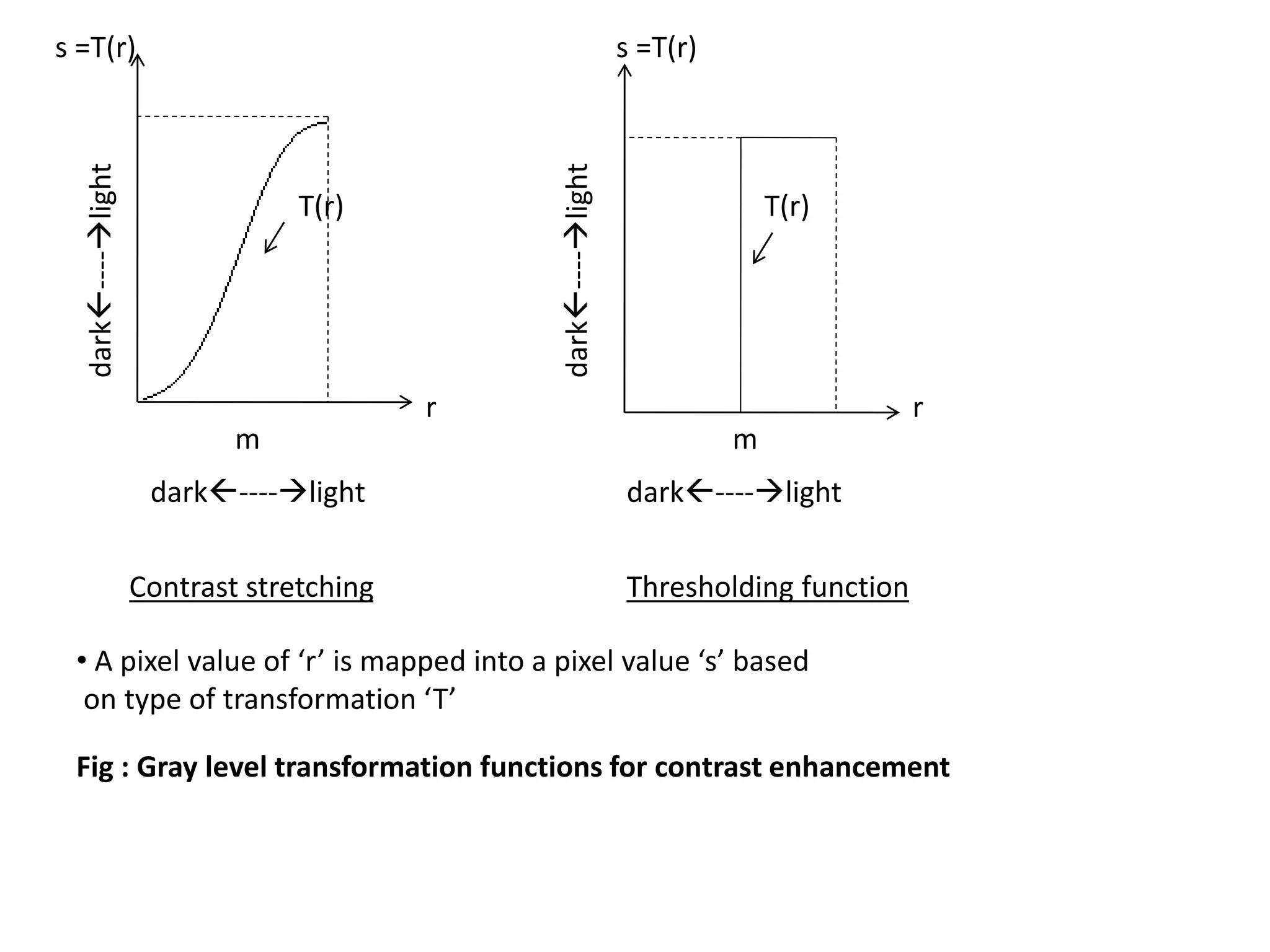
6. BASIC GRAY LEVEL TRANSFORMATIONS
1. IMAGE NEGATIVES
• The negative of an image with gray
levels in the range[0,L-1] is obtained
using negative transformations as in fig.
and the expression is :
s = L-1- r
• This type of processing is particularly suited
for enhancing white or gray detail embedded
in dark regions of an image, especially
when the black area is dominant in size.
0 L-1
L-1
L/2
L/2

7. Fig1: original image Fig2: image negative
Fig1 is the original image and fig2 is the result of the image negative where the dark
region of the image gets converted into the light region .i.e. binary 1 becomes binary 0
and vice versa.
Contd..

8. 2. LOG TRANSFORMATIONS
• The general form of the log transformation is shown in fig and the
expression is :
s = c log (1+r)
where, c is a constant and
assume r ≥ 0
• The shape of the log curve indicates
that the transformation maps a narrow
range of low gray-level values in the
input image into a wider range of
output levels and vice versa.
• It is used for spreading/compressing
of gray levels in an image.
0 L-1L/2
Input gray level, r
outputgraylevel,s
L-1
L/2

9. 3. POWER-LAW TRANSFORMATION
power-law transformation has the basic form:
where, c and r are positive constants.
• The curve generated with the value of γ>1
has exactly the opposite effect as those
generated with γ<1.
• By convention, the exponent in the power
law equation is referred to as gamma. The
process used to correct this power law
response is called gamma correction.
• Images that are not corrected properly can
look either bleached out or too dark.
Input gray level, r
outputgraylevel,s
L/2 L-1
L-1
L/2
0

10. 4. PIECEWISE-LINEAR TRANSFORMATION
1.CONTRAST STRETCHING
Low contrast images can result from poor illumination, lack of
dynamic range in image sensor or even wrong setting of a lens
aperture during image acquisition.
• If r1=s1 & r2=s2, the transformation is
a linear function that produces no change
in gray levels.
• If r1=r2,s1=0&s2=L-1,the transformation
is a thresholding function that creates
binary image.
• Intermediate values of (r1,s1) & (r2,s2)
produces various degrees of spread in gray
levels of output image thus affecting its
contrast.
T(r)
(r2,s2)
(r1,s1)
L-1
L-1
0 L/2
L/2
Input gray level, r
outputgraylevel,s
Fig: transformation used
for contrast stretching

11. Fig1: low contrast image Fig2: high contrast image
Contd..

12. 2. GRAY LEVEL SLICING
There are several ways of doing this technique, but most of them are
variations of two basic themes:
• Display high value for all gray levels in the range of interest and low
values for all other gray values which produces binary image(fig1).
• Brightening the desired range of gray levels but preserving the
background and gray level tonalities in the image(fig2).
T(r)
L-1
L-1
0 B
Input gray level, r
outputgraylevel,s
A
T(r)
A B
Input gray level, r
outputgraylevel,s
0 L-1
L-1

13. 3. BIT-PLANE SLICING
• Focus is on highlighting the contribution
made to total image appearance by
specific bits.
• Higher order bits(top 4) contain
the majority of the visually
significant data.
• Other bit planes contribute to
more subtle details in the image.
One 8-bit byte
Bit plane 0 (LSB)
Fig : Bit plane representation of
an 8 bit image
Bit plane 7(MSB)

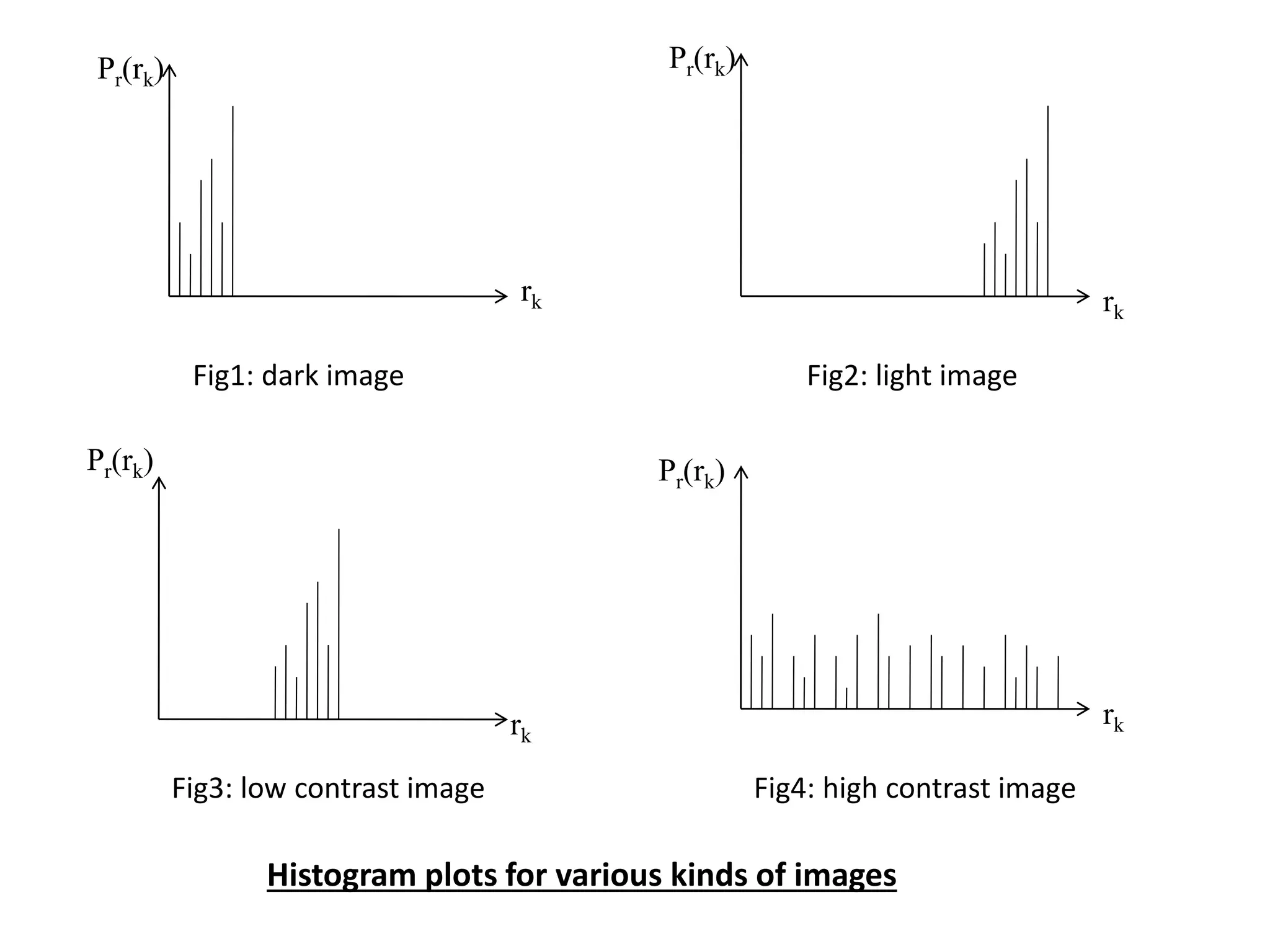
14. HISTOGRAM PROCESSING
• The histogram of a digital image with gray levels in the range[0,L-1]
is a discrete function,
where, rk is the kth gray level & nk is number of pixels in the image
having gray level rk
• Histogram is normalized by dividing each of its values by the total
no. of pixels in the image denoted by ‘n’.
Thus normalized histogram is given by,
where, k = 0,1,2,….L-1
• Histograms are the basis for the numerous spatial domain processing
techniques.
• Histogram manipulation is used effectively for image enhancement,
also quite useful in other image processing applications viz image
compression & segmentation.

15. HISTOGRAM EQUALIZATION
Let us consider the transformation as, S = T(r) , 0 ≤ r ≤ 1
we assume that the transformation function T(r) satisfies the following
conditions :
a. T(r) is single valued and monotonically increasing in the interval
0 ≤ r ≤ 1
b. 0 ≤ T(r) ≤ 1 for 0 ≤ r ≤ 1
• The requirement in (a) guarantees that
the inverse transformation will exist,
and monotonicity condition preserves
the increasing order from black to
white in the output image.
• Condition (b) guarantees that the output
gray levels will be in the same range as
the input levels. Fig : example for a gray level
transformation function i.e.
single valued and monotonically increasing
Sk = T(r k )
0 r
s
r k 1
T(r)
Contd..

16. • The discrete version of the transformation function can be given as :
, k = 0,1,2,…L-1
Thus a processed (output) image is obtained by mapping each pixel with
level rk in the input image into a corresponding pixel with level Sk in the
output image via the above equation.
• A plot of Pr(rk) Vs rk is called histogram. The transformation (mapping)
given in above equation is called histogram equalization or histogram
linearization.
• Histogram equalization automatically determines a transformation function
that seeks to produce an output image has a uniform histogram.
• The method used to generate a processed image that has a specified
histogram is called histogram matching or histogram specification.
Contd..

17. Pr(rk)
Pr(rk)
rk
Pr(rk)
rk
Pr(rk)
rk
rk
Fig1: dark image Fig2: light image
Fig3: low contrast image Fig4: high contrast image
Histogram plots for various kinds of images

18. ENHANCEMENT USING ARITHMETIC/LOGIC
OPERATIONS
• It involves operations performed on a pixel by pixel basis between
two or more images (excluding NOT, which is performed on single
image)
• Any logical operators can be implemented by using only 3 basic
functions(AND, OR & NOT).
• The AND and OR operations are used for masking; i.e. for selecting
subimages in an image. light represents binary1 and dark represents
binary 0.

19. IMAGE SUBTRACTION
The difference between two images f(x,y) and h(x,y) expressed as
g(x,y) = f(x,y) – h(x,y)
The key usefulness of subtraction is the enhancement of differences
between images. Difference is taken between corresponding pixels
of ‘f’ and ‘h’.
Fig3: result of subtractionFig1: image1
The above figure 1 &2 indicates the image taken for subtraction and the figure3 indicates
the result of subtraction of image1 with itself.
-- =
Fig2: image1

20. IMAGE AVERAGING
The purpose of image averaging is noise removal.
Consider a noisy image g(x,y) formed by the addition of noise n(x,y) to an
original image f(x,y); i.e.
g(x,y) = f(x,y) + n(x,y)
If the noise satisfies the constraint (uncorrelated at every coordinate (x,y)),
then averaged image is given by
then it follows that,
E{ } = f(x,y)
i.e. it is expected the averaged image approaches to the original image as the
number of noisy images used in the averaging process increases.

21. f(x-1,
y-1)
f(x-1,y) f(x-1,
y+1)
f(x,y-1) f(x,y) f(x,y-1)
f(x+1,
y-1)
f(x+1,y) f(x+1,
y+1)
BASICS OF SPATIAL FILTERING
W
(-1,-1)
W
(-1,0)
W
(-1,1)
W
(0,-1)
W
(0,0)
W
(0,1)
W
(1,-1)
W
(1,0)
W
(1,1)
mask
Image f(x,y)
y
x
Mask coefficients
Pixels of image section
under mask
Fig: mechanics
of spatial filtering

22. • The process consists of moving the filter mask from point to point in
an image.
• For linear spatial filtering, the response is given by a sum of
products of the filter(mask) coefficients and the corresponding
pixels directly under the mask as:
R = w(-1,-1) f(x-1,y-1) + w(-1,0) f(x-1,y)+……+
w(0,0)f(x,y)+…+……..+w(1,0)f(x+1,y)+w(1,1)f(x+1,y+1).
• In general, linear filtering of an image f of size MxN with a filter
mask of size mxn is given by the expression,
where, a=(m-1)/2 and b=(n-1)/2
• The process of linear filtering is similar to a frequency domain
concept called convolution. for this reason, linear spatial filtering
often is referred to as “convolving a mask with an image”. Filter
masks are sometimes called “convolution masks” or “convolution
kernel”.
Contd..

23. LOCAL ENHANCEMENT
• The histogram processing method are global, i.e. the pixels are
modified by a transformation function based on the gray level
content of an entire image.
• When there is a case to enhance details over small areas in an
image, there will be a problem.
• The solution is to devise a transformation functions based on the
gray level distribution or other properties in the neighborhood of
every pixel in the image. The procedure is to define a square or
rectangular neighborhood & move the center of this area from pixel
to pixel.
• At each location, the histogram of the point in the neighborhood is
computed & either a histogram equalization or histogram
specification transformation function is obtained. This function is
finally used to map the gray level of the pixel centered in the
neighborhood.