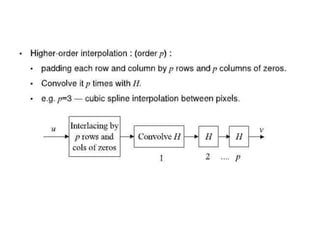
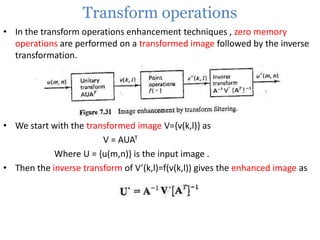
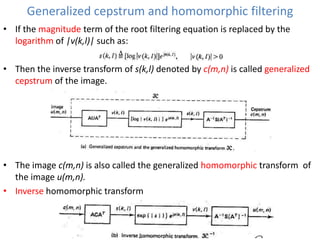
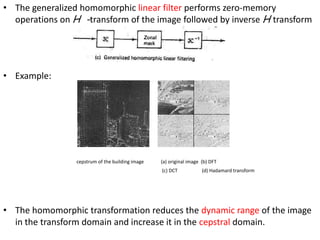
This document provides an overview of various image enhancement techniques. It begins with an introduction to image enhancement and its objectives. It then outlines and describes several categories of enhancement methods, including spatial-frequency domain methods, point operations, histogram operations, spatial operations, and transform operations. Specific techniques discussed in detail include contrast stretching, clipping, thresholding, median filtering, unsharp masking, and principal component analysis for multispectral images. The document also covers color image enhancement and techniques for pseudocoloring.

1. Image Enhancement
Prepared by
Aya Elshiwi
Supervisor
Dr.Osama Ouda

2. outline
• Introduction
• Image enhancement methods:
Spatial-Frequency domain enhancement methods
Point operations
Histogram operations
Spatial operations
Transform operations
• Multi-spectral image enhancement
• False color and pseudocoloring
• Color image enhancement

3. Introduction
• The principal objective of image enhancement is to process a given
image so that the result is more suitable than the original image
for a specific application.
• It accentuates or sharpens image features such as edges,
boundaries, or contrast to make a graphic display more helpful for
display and analysis.
• The enhancement doesn't increase the inherent information
content of the data, but it increases the dynamic range of the
chosen features so that they can be detected easily.

4. Cont.
• The greatest difficulty in image enhancement is quantifying the
criterion for enhancement and, therefore, a large number of
image enhancement techniques are empirical and require
interactive procedures to obtain satisfactory results.
• Image enhancement methods can be based on either spatial or
frequency domain techniques.

5. Spatial-Frequency domain enhancement methods
Spatial domain enhancement methods:
• Spatial domain techniques are performed to the image plane itself and
they are based on direct manipulation of pixels in an image.
• The operation can be formulated as g(x,y) = T[f(x,y)],
where g is the output, f is the input image and T is an operation on f
defined over some neighborhood of (x,y).
• According to the operations on the image pixels, it can be further
divided into 2 categories: Point operations and spatial operations.
Frequency domain enhancement methods:
• These methods enhance an image f(x,y) by convoluting the image with a
linear, position invariant operator.
• The 2D convolution is performed in frequency domain with DFT.
Spatial domain: g(x,y)=f(x,y)*h(x,y)
Frequency domain: G(w1,w2)=F(w1,w2)H(w1,w2)

6. Point operations
-Zero-memory operations where a given gray level u∈[0,L] is mapped
into a gray level v∈[0,L] according to a transformation.
v(m,n)=f(u(m,n))

7. 1-contrast stretching
• The idea behind contrast stretching is to increase the dynamic
range of the gray levels in the image being processed.
• Low contrast images occur often due to :
-poor or nonuniform lightning conditions
-small dynamic range of imaging sensors
• Expressed as :
-For dark region stretch α>1 ,a=L/3
-For mid region stretch β>1 ,b=2/3L
-For bright region stretch γ>1

8. Example 1
• (b) a low-contrast image : results
from poor illumination, lack of
dynamic range in the imaging
sensor, or even wrong setting of
a lens aperture of image
acquisition
• (c) result of contrast stretching :
(r1,s1) = (rmin,0) and (r2,s2) =
(rmax,L-1)
• (d)result of thresholding

9. Example2

10. 2-Clipping and Thresholding
• Expressed as :
• Clipping:
-Special case of contrast stretching ,where α= γ=0
-Useful for noise reduction when the input signal is known to lie in the
range [a,b].

11. Cont.
• Thresholding:
- is a special case of case of clipping where a=b=t and the output
comes binary.
Example 1
Clipping and Thresholding

12. Example2

13. 3-Digital negative
• Negative image can be obtained by reverse scaling of the gray levels
according to the transformation,
v=L-u
• Useful in the display of medical images.
• Example:

14. 4-intensity level slicing
• Permit segmentation of certain gray level regions from the rest of the
image.

15. 5-Bit extraction
• This transformation is useful
In determining the number of
Visually significant bits in an
Image.
• Suppose each pixel is
represented by 8 bits it is desired
To extract the nth most significant bit
And display it .
• Higher-order bits contain the
majority of the visually significant data

16. Example
8-bit fractal image
• The (binary) image for bit-plane 7 can be obtained by processing the
input image with a thresholding gray-level transformation.
-Map all levels between 0 and 127 to 0
-Map all levels between 129 and 255 to 255

17. Cont.
8-bit plane image

18. 6-Range compression
• Sometimes the dynamic range of a processed image far exceeds the
capability of the display device, in which case only the brightest parts
of the images are visible on the display screen.
• An effective way to compress the dynamic range of pixel values is to
perform the following intensity transformation function:
s = c log(1+|u|)
where c is a scaling constant, and the logarithm function performs the
desired compression.

19. 7-Image subtraction and change detection
• In many imaging applications it is desired to compare two
complicated or busy images .
• A simple ,but powerful method is to align the two images and
subtract them .The difference image is then enhanced .
• Applications such as imaging of the blood vessils and arteries in a
body , security monitoring systems .
• Example:
_

20. Histogram modeling
Histogram modeling techniques modify an image so that it’s histogram has a
desired shape . This is useful in stretching the low contrast levels with
narrow histograms .
It is possible to develop a transformation function that can automatically
achieve this effect ,based on histogram of input image .

21. Histogram modeling Cont.
Image Histogram

22. 1-Histogram equalization
• The objective is to map an input image to an output image such that
its histogram is uniform after the mapping.
• Let r represent the gray levels in the image to be enhanced and s is
the enhanced output with a transformation of the form s=T(r).
• Assumptions
• Possible for multiple values of r to map to a single value of s.

23. Histogram Equalization cont.
Example 1:

24. Solution

25. Solution cont.

26. Solution cont.

27. Example 2: Equalizing an image of 6 gray levels

29. Histogram specification
• Histogram equalization only generates an approximation to a uniform
histogram.
• With Histogram Specification, we can specify the shape of the
histogram that we wish the output image to have.
• It doesn’t have to be a uniform histogram.
• The principal difficulty in applying the histogram specification
method to image enhancement lies in being able to construct a
meaningful histogram.

30. Histogram specification cont.

31. Histogram specification cont.
Procedure :

32. Example

33. Example cont.

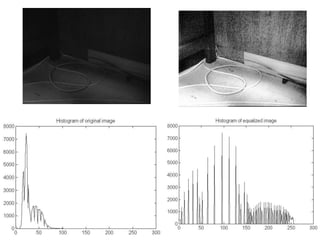
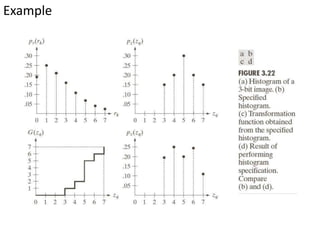
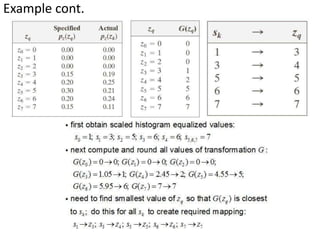
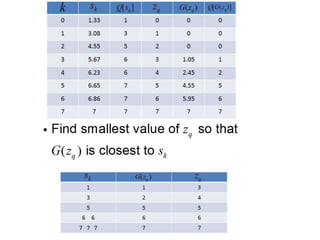
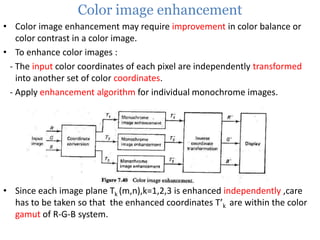
35. Spatial operations
• Operations performed on local neighborhoods of input pixels
• Image is convolved with [FIR] finite impulse response filter called
spatial mask .
• Techniques such as :
- Noise smoothing
- Median filtering
- LP,HP &PB filtering
- Zooming

36. Spatial averaging and spatial low-pass filtering
•
Each pixel is replaced by a weighted average of it’s neighborhood pixels
that is,
-y(m,n) and v(m,n) are the input and output images ,respectively.
-W is suitably chosen window .
-a(k,l) are the filter weights .
• A common class of spatial averaging filters has all equal weights,
• Used for Noise smoothing , low-pass filtering and subsampling of images.

37. • Examples of spatial averaging masks
• Spatial averaging is used for Noise smoothing

38. Example

39. directional smoothing
• To protect edges from blurring while smoothing.
•
spatial averages are calculated in several directions , and the direction
giving the smallest changes before and after filtering is selected.
• The direction (θ) is found such that
• Then
gives the desired result.
is minimum

40. Median filtering
• Input pixel is replaced by the median of the pixels contained in a window
around a pixel
• The algorithm requires arranging the pixels in an increasing or decreasing
order and picking the middle value.
• For Odd window size is commonly used [3*3-5*5-7*7]
• For even window size the average of two middle values is taken.
• Median filter properties:
1- Non-linear filter
2-Performes very well on images containing binary noise , poorly when the
noise is gaussian.
3-performance is poor in case that the number of noise pixels in the window is
greater than or half the number of pixels in the window.

41. Example:

42. Example 2:

43. Unsharp masking and crispening
• The unsharp masking techniques is used commonly in printing industry for
crispening the edges.
• It is applied by subtracting an unsharp or smoothed or low-pass filtered version of
an image from the original image.
• It is equivalent to adding the gradient, or high-pass signal to the image as shown in
figure.
Unsharp masking operations

44. Unsharp masking and crispening cont.
• Unsharp masking operation can be represented by :
v(m,n) = u(m,n) + λg(m,n)
Where λ > 0 and g(m,n) is a suitably defined gradient at (m,n).
• A commonly used gradient function is the discrete laplacian.

45. Example : unsharp masking using laplacian operator

46. Spatial low-pass ,high-pass and band-pass Filtering
• Spatial averaging operations is a low-pass filter.
• High-pass filter can be implemented by subtracting low-pass filter output
from it’s input.
• Band-pass filter can be characterized as:
where hl1 ,hl2 represent short and long term averages.

47. • Low-pass filters are useful for noise smoothing and interpolation .
• High-pass Filters are useful in extracting edges and in sharpening images.
• Band-pass filters are useful in the enhancement of edges and other highpass image characteristics in the presence of noise .
• Example1

48. • Example2

49. Inverse contrast mapping and statistical scaling
• The ability of our visual system to detect an object in a uniform background
depends on it’s size and the contrast ratio which is defined as
γ
= σ/ μ
• where μ is the average luminance of object σ is the standard deviation of the
luminance of the object plus it’s surround.
• Now consider the inverse contrast ratio transformation
Where μ(m,n) and σ(m,n) are the local mean and standard deviation of u(m,n)
measured over a window W and are given by:
• This transformation generates an image ,where the weak(low-contrast) edges are
enhanced.

50. • A special case of this transformation
•
which scales each pixel by it’s standard deviation to generate an image
whose pixels have unity variance .
• This mapping is also called statistical scaling.
• Example:

51. Magnification and interpolation (zooming)
• Often it is desired to zoom on a given region of an image .This requires
taking an image and displaying it as a larger image .
• Techniques : -Replication
-linear interpolation

52. Zooming by Replication

53. • Example

54. Zooming by interpolation

55. • Example

57. Transform operations
• In the transform operations enhancement techniques , zero memory
operations are performed on a transformed image followed by the inverse
transformation.
• We start with the transformed image V={v(k,l)} as
V = AUAT
Where U = {u(m,n)} is the input image .
• Then the inverse transform of V’(k,l)=f(v(k,l)) gives the enhanced image as

58. Generalized linear Filtering
• The zero memory transform domain operation is a pixel by pixel
multiplication .
Where g(k,l) is called a zonal mask.

60. • A filter of special interest is the inverse gaussian filter ,whose zonal mask for
N.N images is defined as:
When A is a DFT.
• For other orthogonal transforms the gaussian zonal mask is used as :
• Usually, the inverse Gaussian filter is used as high-frequency filter that
restore the blurred images.
Example:
Inverse gaussian Filtering

61. Root Filtering
• The transform coefficients v(k,l) can be written as:
• In root filtering, the α-root of the magnitude component of v(k,l) is taken,
while retaining the phase component, to yield
• For common images, since the magnitude of v(k,l) is relatively smaller at
higher frequencies, the effect of α -rooting is to enhance higher frequencies
(low amplitudes) relative to lower frequencies (high amplitudes).
• The following figure shows the effect of these filters

62. Generalized cepstrum and homomorphic filtering
• If the magnitude term of the root filtering equation is replaced by the
logarithm of |v(k,l)| such as:
• Then the inverse transform of s(k,l) denoted by c(m,n) is called generalized
cepstrum of the image.
• The image c(m,n) is also called the generalized homomorphic transform of
the image u(m,n).
• Inverse homomorphic transform

63. • The generalized homomorphic linear filter performs zero-memory
operations on H -transform of the image followed by inverse H transform
• Example:
cepstrum of the building image
(a) original image (b) DFT
(c) DCT
(d) Hadamard transform
• The homomorphic transformation reduces the dynamic range of the image
in the transform domain and increase it in the cepstral domain.

64. Multispectral image enhancement
• In multispectral imaging there is a sequence of I images Ui(m,n) ,i=0,1,2….L
where L is typically between 2 and 12.
• It is desired to combine these images to generate a single or a few display
images that are representative of their features.
• Three methods to enhance such images:
-Intensity ratios
-Log ratios
-Principal components

65. Intensity ratios
•
Define the ratios:
• Where ui(m,n) represents the intensity and is assumed to be positive.
• This methods gives I2-I combinations for the ratios the most suitable of
which are chosen by visual inspection.
• Sometimes the ratios are defined with respect to the average image
to reduce the number of combinations.

66. Log ratios
• Taking logarithm of both sides
• The log ratio Li,j gives a better display when the dynamic range of Ri,j is very
large which can occur if the spectral features at a spatial location are quite
different.

67. Principal components
• For each (m,n) define I*1 vector
• The I*I KL transform of u(m,n) denoted by (Φ) is determined from auto correlation matrix of the ensemble of vectors {ui(m,n),i=0…I}.
• The rows of (Φ)which are eigen vectors of the auto correlation matrix are
arranged in decreasing order of their associated eigen values .
• Then for any I0<I,the images vi(m,n),i=0….I0 obtained from the KL
transformed vector.

68. False color and pseudocolor
-Human can distinguish more colors than gray levels.
-False color: mapping a color image into another color image to provide a more
striking color contrast e.g to attract attention of human.
-pseudocoloring : mapping a set of images into a color image .
usually different features represented by different color.
Pseudocolor image enhancement

69. • Other methods are possible ,including a pseudorandom mapping of gray
levels into R,G,B coordinates , as is done in some image display systems.
• For image data set where the number of images is greater than or equal to
three , the data set can be reduced to three ratios, three log-ratios or three
principle components , which are then mapped into suitable colors.
•
In general, the pseudocolor mappings are nonunique , and extensive
interactive trials may be required to determine an acceptable mapping for
displaying a given set of data.

70. Color image enhancement
• Color image enhancement may require improvement in color balance or
color contrast in a color image.
• To enhance color images :
- The input color coordinates of each pixel are independently transformed
into another set of color coordinates.
- Apply enhancement algorithm for individual monochrome images.
• Since each image plane Tk (m,n),k=1,2,3 is enhanced independently ,care
has to be taken so that the enhanced coordinates T’k are within the color
gamut of R-G-B system.

71. Questions ?