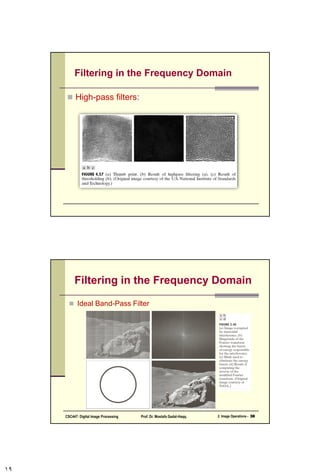
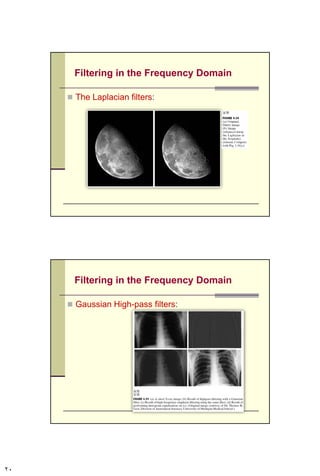
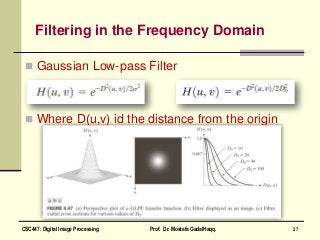
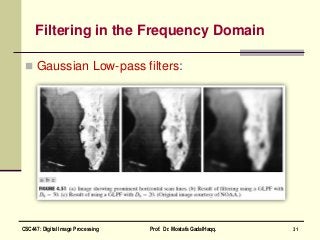
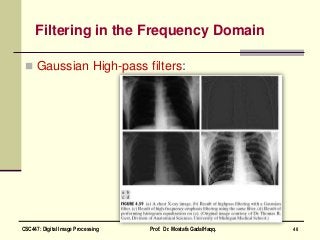
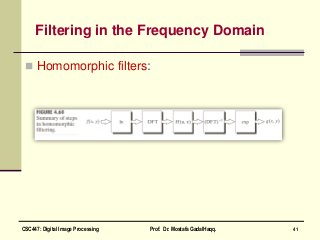
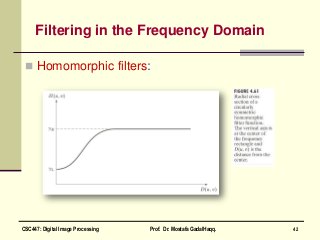
This document is a chapter from a textbook on digital image processing. It discusses the discrete Fourier transform (DFT) and its properties. It also covers various filtering techniques that can be performed in the frequency domain, including low-pass, high-pass, band-pass, and homomorphic filters using approaches like Gaussian, Butterworth, and ideal filters. Homework problems 4.9 and 4.12 are also mentioned at the end.


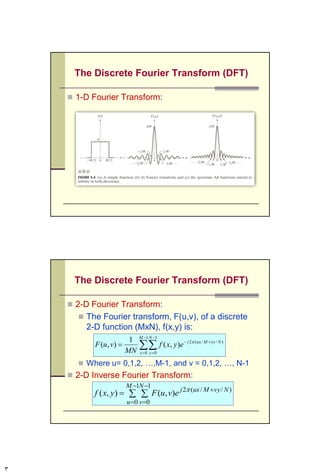
([tan(u)and,)]()([|)(|where,
|)(|)(
1-2/122
)(
uRuIuIuRuF
euFuF uj
4CSC447: Digital Image Processing Prof. Dr. Mostafa GadalHaqq.](https://image.slidesharecdn.com/csc447dipch4-160628142957/85/Digital-Image-Processing-Image-Enhancement-in-the-Frequency-Domain-4-320.jpg)
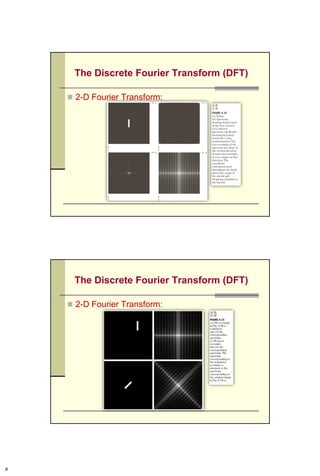

![The Discrete Fourier Transform (DFT)
the Fourier spectrum , phase angle, andpower
spectrum , are defined as before:
),(),(|),(|
and)],,(/),([tanv)(u,
,)],(),([|),(|where,
|),(|),(
222
1-
2/122
),(
vuIvuRvuFP(u,v)
vuRvuI
vuIvuRvuF
evuFvuF vuj
7CSC447: Digital Image Processing Prof. Dr. Mostafa GadalHaqq.](https://image.slidesharecdn.com/csc447dipch4-160628142957/85/Digital-Image-Processing-Image-Enhancement-in-the-Frequency-Domain-7-320.jpg)