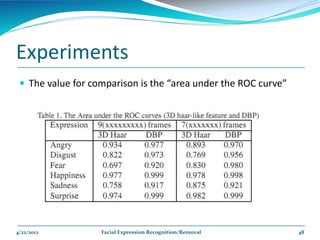
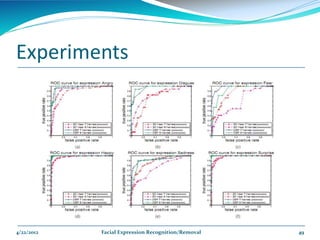
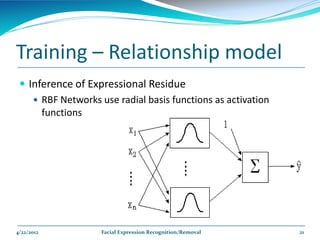
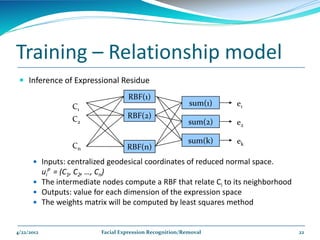
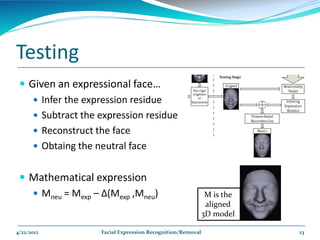
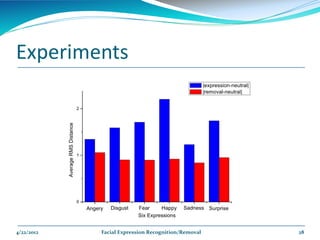
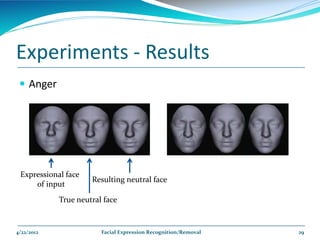
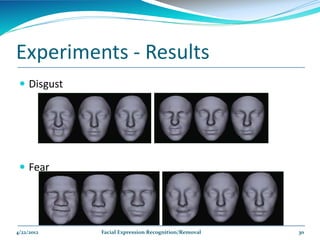
The document describes a framework for facial expression recognition and removal from 3D face models. The framework involves aligning an expressional 3D face to a generic model, building normal and expression residue spaces through training data, learning the relationship between these spaces using RBF regression to infer expressions, and reconstructing a neutral face by subtracting the inferred expression from the input face. The method is evaluated on the BU-3DFE database and shown to effectively recognize and remove expressions, reconstructing neutral faces.
































![Building our Experts
A normalized histogram is calculated, considering all the
features in the sequence
Ex for 7 features: [0 0 1/7 2/7 4/7]
4/22/2012 Facial Expression Recognition/Removal 40](https://image.slidesharecdn.com/projectpresentation1-120422233618-phpapp01/85/Facial-Expression-Recognition-Removal-40-320.jpg)
![Building our Experts
We will convert the binary vector to decimal
[ 0/7 0/7 1/7 2/7 4/7 ]
= [ 1 2 4 8 16 ]
= 0 + 0 + 4/7 + 16/7 + 64/7 = 84/7 = 12
4/22/2012 Facial Expression Recognition/Removal 41](https://image.slidesharecdn.com/projectpresentation1-120422233618-phpapp01/85/Facial-Expression-Recognition-Removal-41-320.jpg)