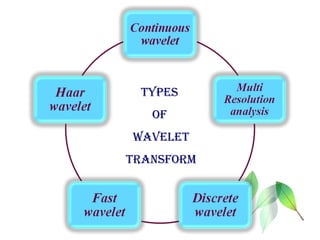
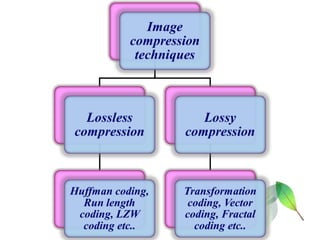
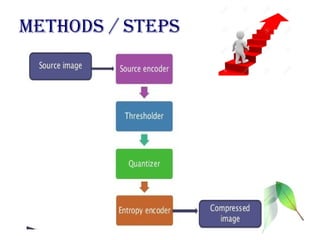
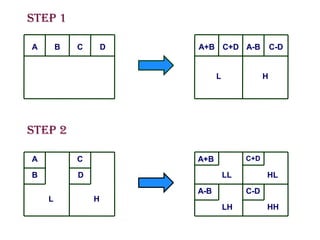
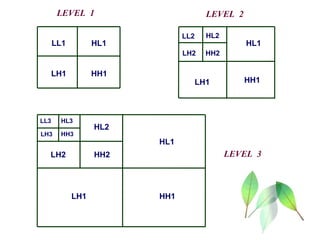
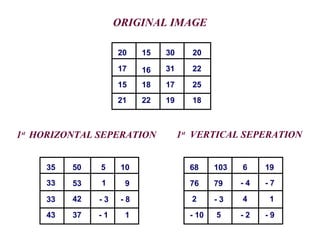
The document discusses wavelet transform as a technique for image compression, highlighting its historical development and methodology. It explains the advantages of using wavelets, such as better compression ratios and the ability to maintain image quality without introducing blocking artifacts. Additionally, it explores various applications of wavelet transforms across different fields, affirming their effectiveness and significance in digital image processing.

1. WAVELET TRANSFORM
IN
IMAGE COMPRESSION
Presented By,
E . JEEVITHA
16MMAT05
M.Phil Mathematics

2. OVERVIEW
Introduction
Historical developments
Techniques
Methodology
Applications
Advantages
Conclusion

3. INTRODUCTION
Wavelets are mathematical functions that splits
up data into different frequency components, and
then study each component with a resolution
matched to its scale.
Wavelet transform decomposes a signal into a
set of basis functions. These basis functions are
called as “ wavelets ”.

4. HISTORICAL DEVELOPMENTS
1909 : Alfred Haar – Dissertation “On the orthogonal
function systems” for his doctoral degree. The first wavelet
related theory.
1910 : Alfred Haar : Development of a set of rectangular
basis functions.
1930 : Paul Levy investigated “ The brownian motion”.
Littlewood and Paley worked on localizing the
contributing energies of a functon.
1946 : Dennis Gabor : Used short time fourier transform.

5. 1975 : George zweig - The first continuous wavelet
transform.
1985 : Meyer - Construction of orthogonal wavelet basis
functions with very good time and frequency localization.
1986 : Stephen Mallet – Developing the idea of Multi-
resolution analysis for DWT.
1988 : Daubechies and Mallet – The modern wavelet
theory.
1992 : Albert cohen and Daubechies constructed the
compactly supported biorthogonal wavelets.

6. TYPES
OF
WAVELET
TRANSFORM

7. WHY IMAGE COMPRESSION?
Digital images usually require a very
large number of bits, this causes critical
problem for digital image data
transmission and storage.
It is the art & science of reducing the
amount of data required to represent an
image.
It is one of the most useful and
commercially successful technologies in
the field of digital image processing.

9. WHY WAVELETS ?
Good approximation properties.
Efficient way to compress the
smooth data except in localized
region.
Easy to control wavelet properties.
( Example : Smoothness, better
accuracy near sharp gradients).

10. METHODS / STEPS

11. Digitize the source image to a signal s, which is a
string of numbers.
Decompose the signal into a sequence of wavelet
coefficients.
Use thresholding to modify the wavelet compression
from w to another sequence w’.
Use quantization to convert w’ to a sequence q.
Apply entropy coding to compress q into a sequence e.

12. A B C D A+B C+D A-B C-D
L H
STEP 1
STEP 2
A
B
C
D
L H
A+B
A-B
C+D
C-D
LL
LH
HL
HH

13. LL1
LH1
HL1
HH1
HL1
HH1LH1
LH1 HH1
HL1
HH2
HL2
LH2
HH2LH2
LL2 HL2
LL3 HL3
LH3 HH3
LEVEL 1 LEVEL 2
LEVEL 3

14. ORIGINAL IMAGE
20 15 30 20
17 16 31 22
15 18 17 25
21 22 19 18
35 50 5 10
33 53 1 9
33 42 - 3 - 8
43 37 - 1 1
68 103 6 19
76 79 - 4 - 7
2 - 3 4 1
- 10 5 - 2 - 9
1st
HORIZONTAL SEPERATION 1st
VERTICAL SEPERATION

15. APPLICATION

16. LL2 HL2
LH2 HH2
LH
HL
HH
LH
HL
HH
HL2
LH2 HH2
LL3 HL3
LH3 HH3

17. OTHER APPLICATIONS
Wavelets are a powerful statistical tool which can
be used for a wide range of applications, namely
Signal processing.
Image processing.
Smoothing and image denoising.
Fingerprint verification.
Biology for cell membrane recognition, to
distinguish the normal from the pathological
membranes.

18. DNA analysis, protein analysis.
Blood-pressure, heart-rate and ECG analysis.
Finance (which is more surprising), for
detecting the properties of quick variation of values.
In Internet traffic description, for
designing the services size.
Speech recognition.
Computer graphics and multi-fractal
analysis.

19. ADVANTAGES
The advantage of wavelet compression is that, in contrast
to JPEG, wavelet algorithm does not divide image into
blocks, but analyze the whole image.
Wavelet transform is applied to sub images, so it produces
no blocking artifacts.
Wavelets have the great advantage of being able to
separate the fine details in a signal.
Wavelet allows getting best compression ratio, while
maintaining the quality of the images.

20. CONCLUSION
Image compression using wavelet transforms results
in an improved compression ratio as well as image quality.
Wavelet transform is the only method that provides both
spatial and frequency domain information. These
properties of wavelet transform greatly help in
identification and selection of significant and non-
significant coefficient. Wavelet transform techniques
currently provide the most promising approach to high
quality image compression, which is essential for many
real world applications.

21. THANK YOU