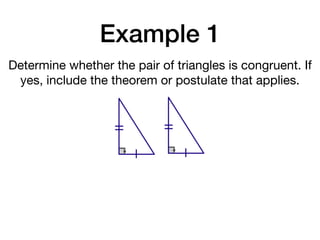
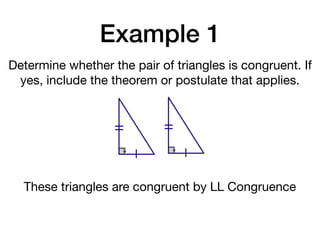
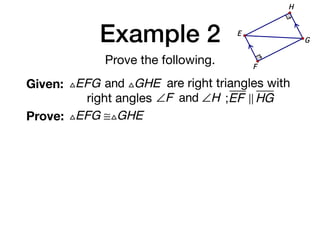
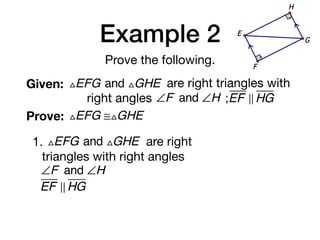
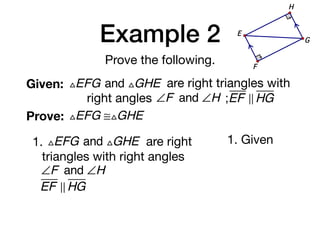
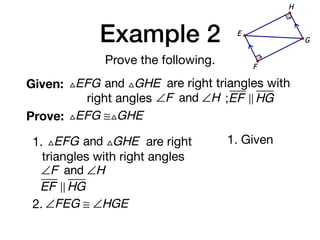
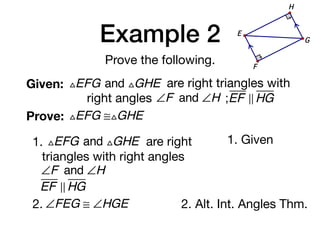
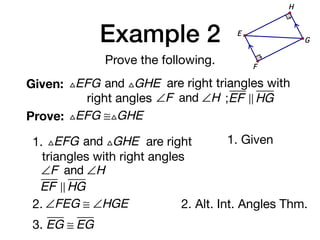
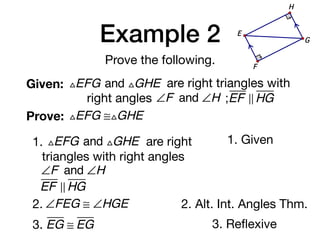
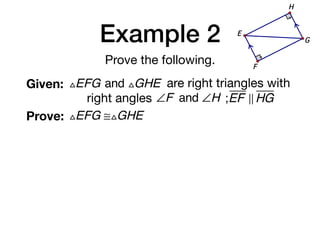
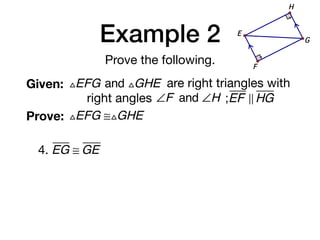
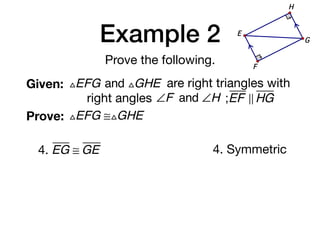
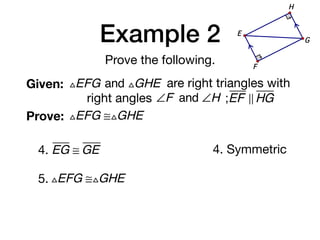
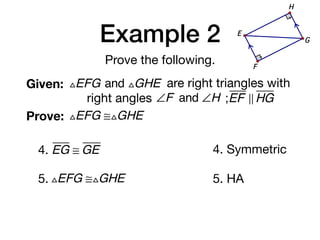
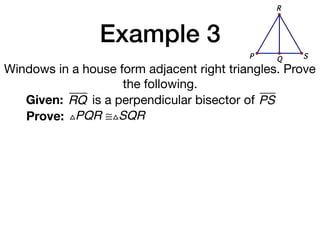
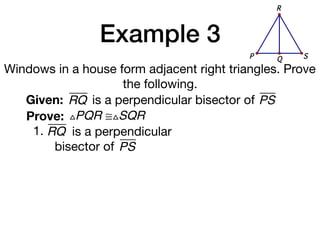
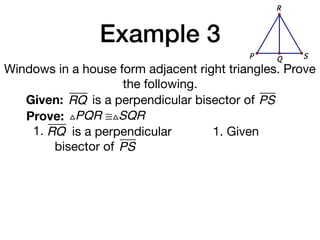
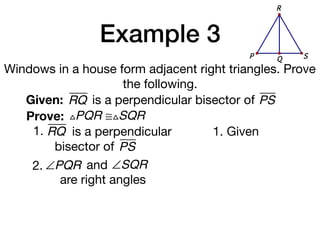
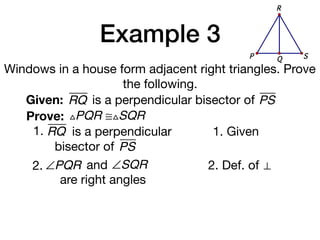
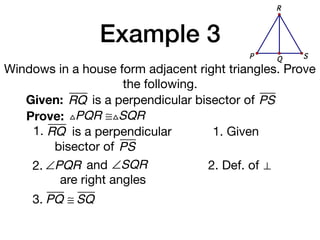
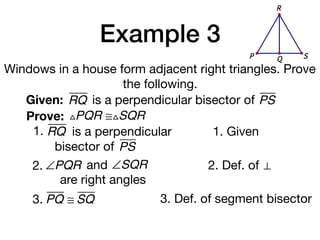
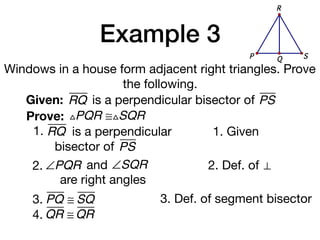
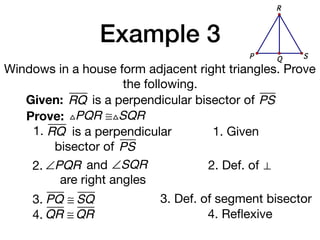
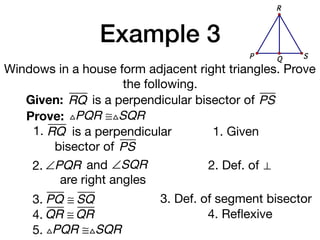
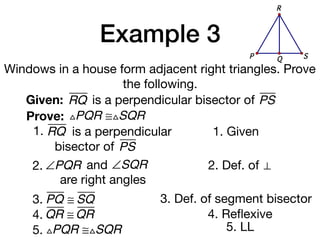
The document discusses four right triangle congruence theorems: leg-leg (LL), hypotenuse-angle (HA), leg-angle (LA), and hypotenuse-leg (HL). It then provides three examples of proving right triangles congruent using these theorems, showing the steps of the proofs.

1. Section 4-5
Proving Right Triangles Congruent

2. Essential Question
• How do you use the right triangle congruence
theorems to prove relationships on geometric
figures?

3. Leg-Leg Congruence (LL)
If the legs of one right triangle are congruent to the
corresponding legs of a second right triangle, then the
triangles are congruent.

4. Hypotenuse-Angle
Congruence (HA)
If the hypotenuse and acute angle of one right triangle
are congruent to the hypotenuse and corresponding
acute angle of another right triangle, then the two
triangles are congruent.

5. Leg-Angle Congruence (LA)
If one leg and an acute angle of one right triangle are
congruent to the corresponding leg and acne angle of
second right triangle, then the triangles are congruent.

6. Hypotenuse -Leg
Congruence (HL)
If the hypotenuse and a leg of one right triangle are
congruent to the hypotenuse and corresponding leg of
another right triangle, then the triangles are congruent.

7. Example 1
Determine whether the pair of triangles is congruent. If
yes, include the theorem or postulate that applies.

8. Example 1
Determine whether the pair of triangles is congruent. If
yes, include the theorem or postulate that applies.
These triangles are congruent by LL Congruence

9. Example 2
Prove the following.
Given: △EFG and △GHE are right triangles with
right angles ∠F and ∠H ;EF ! HG
Prove: △EFG ≅△GHE
G
E
F
H

10. Example 2
Prove the following.
Given: △EFG and △GHE are right triangles with
right angles ∠F and ∠H ;EF ! HG
Prove: △EFG ≅△GHE
G
E
F
H
1. △EFG and △GHE are right
triangles with right angles
∠F and ∠H
EF ! HG

11. Example 2
Prove the following.
Given: △EFG and △GHE are right triangles with
right angles ∠F and ∠H ;EF ! HG
Prove: △EFG ≅△GHE
G
E
F
H
1. △EFG and △GHE are right
triangles with right angles
∠F and ∠H
EF ! HG
1. Given

12. Example 2
Prove the following.
Given: △EFG and △GHE are right triangles with
right angles ∠F and ∠H ;EF ! HG
Prove: △EFG ≅△GHE
G
E
F
H
1. △EFG and △GHE are right
triangles with right angles
∠F and ∠H
EF ! HG
1. Given
2. ∠FEG ≅ ∠HGE

13. Example 2
Prove the following.
Given: △EFG and △GHE are right triangles with
right angles ∠F and ∠H ;EF ! HG
Prove: △EFG ≅△GHE
G
E
F
H
1. △EFG and △GHE are right
triangles with right angles
∠F and ∠H
EF ! HG
1. Given
2. ∠FEG ≅ ∠HGE 2. Alt. Int. Angles Thm.

14. Example 2
Prove the following.
Given: △EFG and △GHE are right triangles with
right angles ∠F and ∠H ;EF ! HG
Prove: △EFG ≅△GHE
G
E
F
H
1. △EFG and △GHE are right
triangles with right angles
∠F and ∠H
EF ! HG
1. Given
2. ∠FEG ≅ ∠HGE 2. Alt. Int. Angles Thm.
3. EG ≅ EG

15. Example 2
Prove the following.
Given: △EFG and △GHE are right triangles with
right angles ∠F and ∠H ;EF ! HG
Prove: △EFG ≅△GHE
G
E
F
H
1. △EFG and △GHE are right
triangles with right angles
∠F and ∠H
EF ! HG
1. Given
2. ∠FEG ≅ ∠HGE 2. Alt. Int. Angles Thm.
3. EG ≅ EG 3. Reflexive

16. Example 2
Prove the following.
Given: △EFG and △GHE are right triangles with
right angles ∠F and ∠H ;EF ! HG
Prove: △EFG ≅△GHE
G
E
F
H

17. Example 2
Prove the following.
Given: △EFG and △GHE are right triangles with
right angles ∠F and ∠H ;EF ! HG
Prove: △EFG ≅△GHE
G
E
F
H
4. EG ≅ GE

18. Example 2
Prove the following.
Given: △EFG and △GHE are right triangles with
right angles ∠F and ∠H ;EF ! HG
Prove: △EFG ≅△GHE
G
E
F
H
4. EG ≅ GE 4. Symmetric

19. Example 2
Prove the following.
Given: △EFG and △GHE are right triangles with
right angles ∠F and ∠H ;EF ! HG
Prove: △EFG ≅△GHE
G
E
F
H
4. EG ≅ GE 4. Symmetric
5. △EFG ≅△GHE

20. Example 2
Prove the following.
Given: △EFG and △GHE are right triangles with
right angles ∠F and ∠H ;EF ! HG
Prove: △EFG ≅△GHE
G
E
F
H
4. EG ≅ GE 4. Symmetric
5. △EFG ≅△GHE 5. HA

21. Example 3
Windows in a house form adjacent right triangles. Prove
the following.
Given: RQ
Prove: △PQR ≅△SQR
is a perpendicular bisector of PS
QP S
R

22. Example 3
Windows in a house form adjacent right triangles. Prove
the following.
Given: RQ
Prove: △PQR ≅△SQR
is a perpendicular bisector of PS
1. RQ is a perpendicular
bisector of PS
QP S
R

23. Example 3
Windows in a house form adjacent right triangles. Prove
the following.
Given: RQ
Prove: △PQR ≅△SQR
1. Given
is a perpendicular bisector of PS
1. RQ is a perpendicular
bisector of PS
QP S
R

24. Example 3
Windows in a house form adjacent right triangles. Prove
the following.
Given: RQ
Prove: △PQR ≅△SQR
1. Given
is a perpendicular bisector of PS
1. RQ is a perpendicular
bisector of PS
QP S
R
2. ∠PQR and ∠SQR
are right angles

25. Example 3
Windows in a house form adjacent right triangles. Prove
the following.
Given: RQ
Prove: △PQR ≅△SQR
1. Given
2. Def. of ⊥
is a perpendicular bisector of PS
1. RQ is a perpendicular
bisector of PS
QP S
R
2. ∠PQR and ∠SQR
are right angles

26. Example 3
Windows in a house form adjacent right triangles. Prove
the following.
Given: RQ
Prove: △PQR ≅△SQR
1. Given
2. Def. of ⊥
3. PQ ≅ SQ
is a perpendicular bisector of PS
1. RQ is a perpendicular
bisector of PS
QP S
R
2. ∠PQR and ∠SQR
are right angles

27. Example 3
Windows in a house form adjacent right triangles. Prove
the following.
Given: RQ
Prove: △PQR ≅△SQR
1. Given
2. Def. of ⊥
3. PQ ≅ SQ 3. Def. of segment bisector
is a perpendicular bisector of PS
1. RQ is a perpendicular
bisector of PS
QP S
R
2. ∠PQR and ∠SQR
are right angles

28. Example 3
Windows in a house form adjacent right triangles. Prove
the following.
Given: RQ
Prove: △PQR ≅△SQR
1. Given
2. Def. of ⊥
3. PQ ≅ SQ 3. Def. of segment bisector
is a perpendicular bisector of PS
1. RQ is a perpendicular
bisector of PS
QP S
R
2. ∠PQR and ∠SQR
are right angles
4. QR ≅ QR

29. Example 3
Windows in a house form adjacent right triangles. Prove
the following.
Given: RQ
Prove: △PQR ≅△SQR
1. Given
2. Def. of ⊥
3. PQ ≅ SQ 3. Def. of segment bisector
is a perpendicular bisector of PS
1. RQ is a perpendicular
bisector of PS
QP S
R
2. ∠PQR and ∠SQR
are right angles
4. QR ≅ QR 4. Reflexive

30. Example 3
Windows in a house form adjacent right triangles. Prove
the following.
Given: RQ
Prove: △PQR ≅△SQR
1. Given
2. Def. of ⊥
3. PQ ≅ SQ 3. Def. of segment bisector
is a perpendicular bisector of PS
1. RQ is a perpendicular
bisector of PS
QP S
R
2. ∠PQR and ∠SQR
are right angles
4. QR ≅ QR 4. Reflexive
5. △PQR ≅△SQR

31. Example 3
Windows in a house form adjacent right triangles. Prove
the following.
Given: RQ
Prove: △PQR ≅△SQR
1. Given
2. Def. of ⊥
3. PQ ≅ SQ 3. Def. of segment bisector
is a perpendicular bisector of PS
1. RQ is a perpendicular
bisector of PS
QP S
R
2. ∠PQR and ∠SQR
are right angles
4. QR ≅ QR 4. Reflexive
5. △PQR ≅△SQR 5. LL