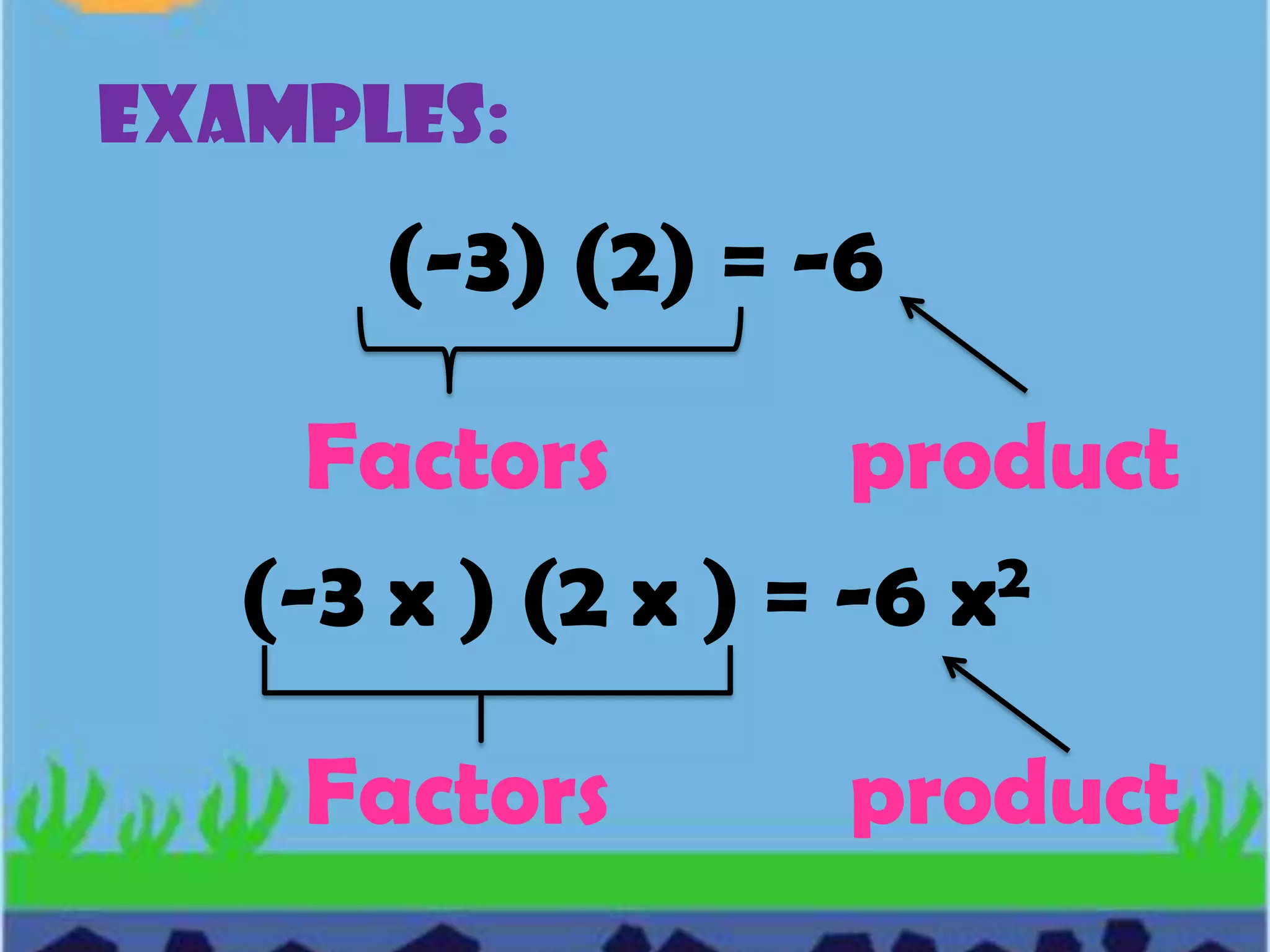
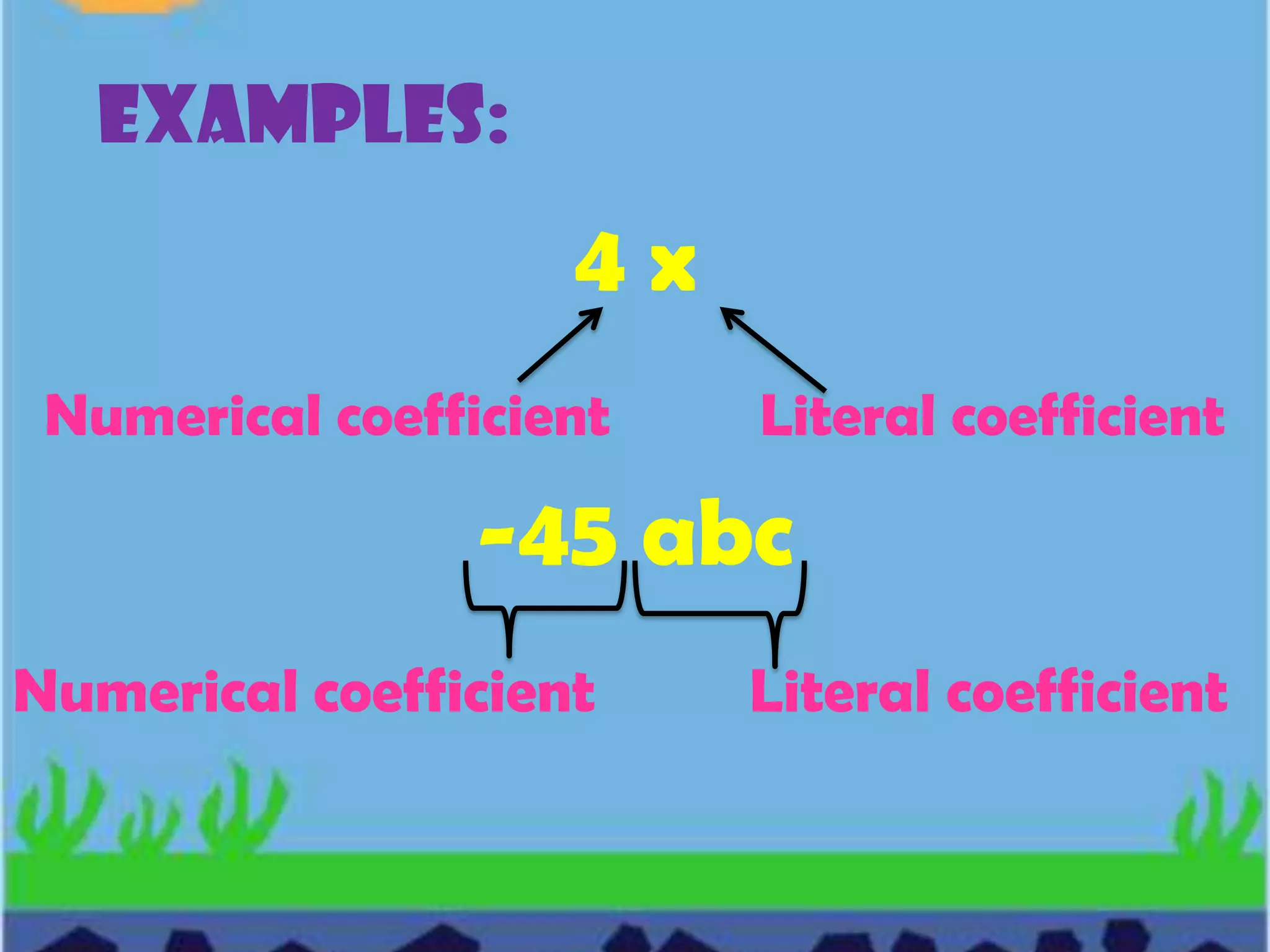
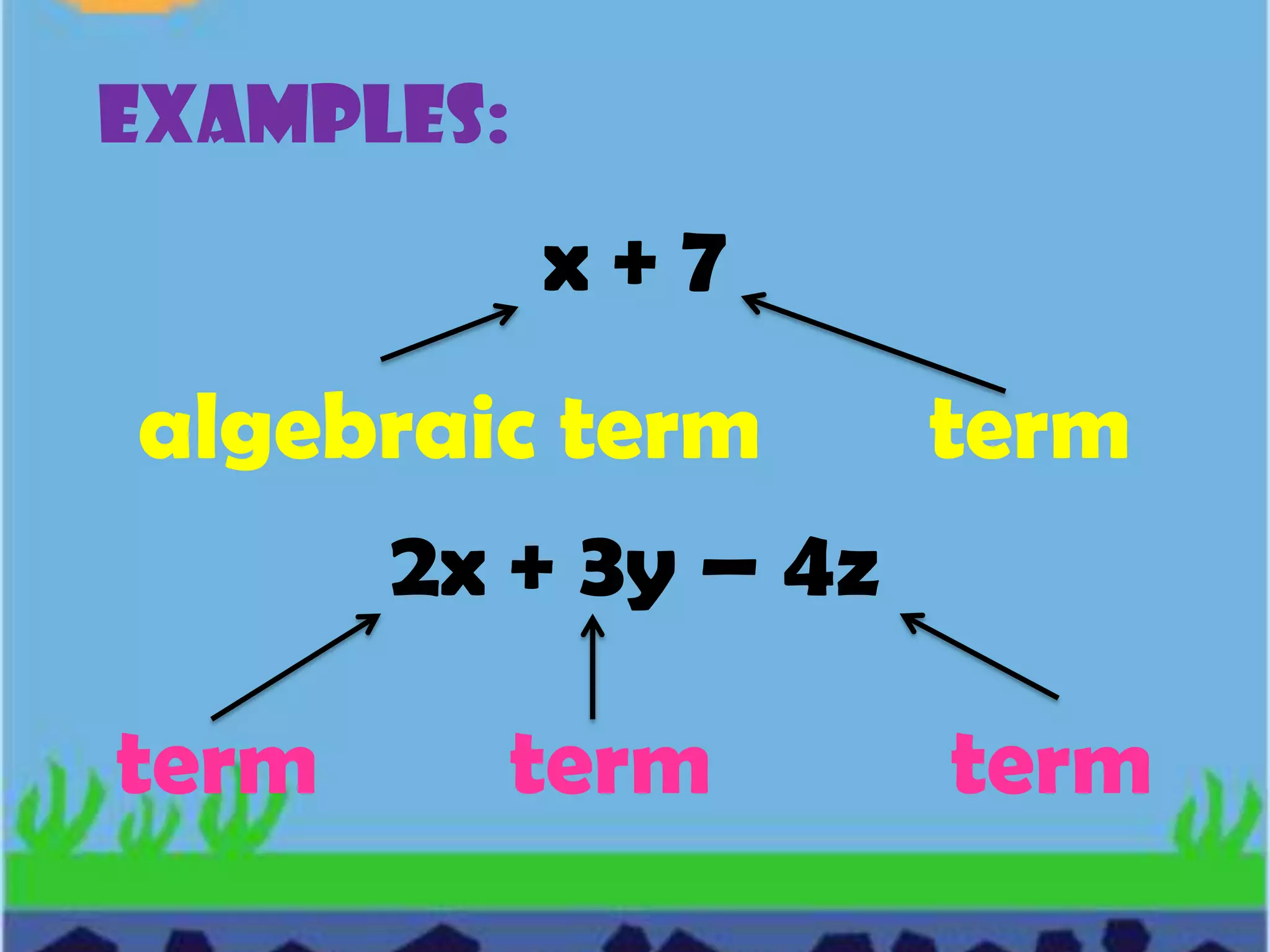
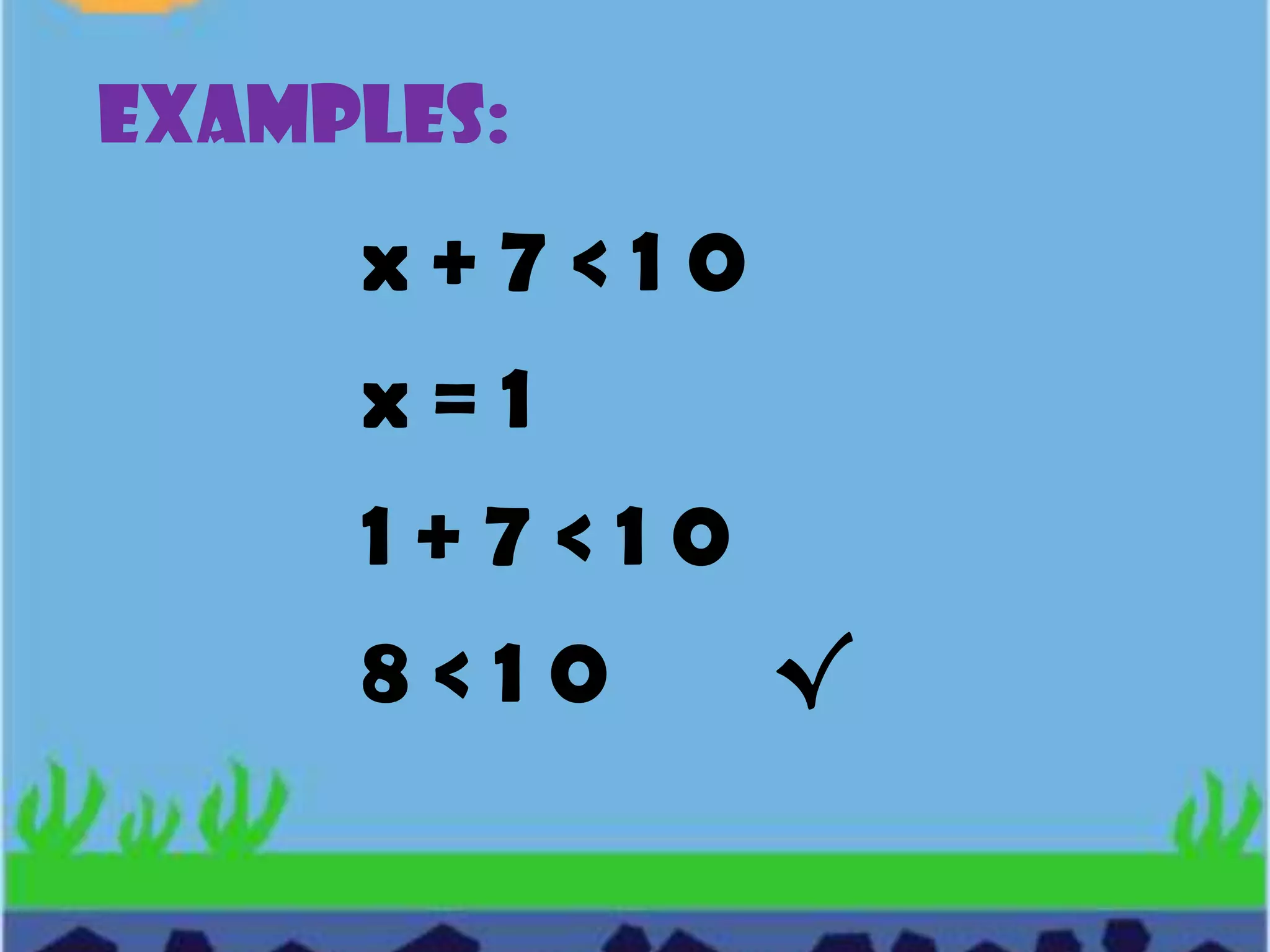Algebra is a branch of mathematics that uses letters and symbols to represent numbers and quantities in expressions and equations. Key terms in algebra include variables, which can represent different numbers; replacement sets, which define the possible values a variable can take; and constants, which always represent the same number. Algebraic expressions combine variables, constants, and operation symbols using grouping symbols and relationship symbols to represent a mathematical relationship between quantities.









![= 3. 141592654…SYMBOLS OF GROUPINGParentheses: ( )Brackets: [ ]Braces: { }Bar or fraction bar: ____](https://image.slidesharecdn.com/algebraicexpression-111015055543-phpapp01/75/Algebraic-expression-10-2048.jpg)
![EXAMPLES:1 1 – { 1 2 – [ 4 – (8 + 9 ) ] – 1 3 }1 1 – { 1 2 – [ 4 – 1 7 ] – 1 3 }1 1 – { 1 2 – 1 3 + 1 3 }1 1 – 1 2- 1](https://image.slidesharecdn.com/algebraicexpression-111015055543-phpapp01/75/Algebraic-expression-11-2048.jpg)