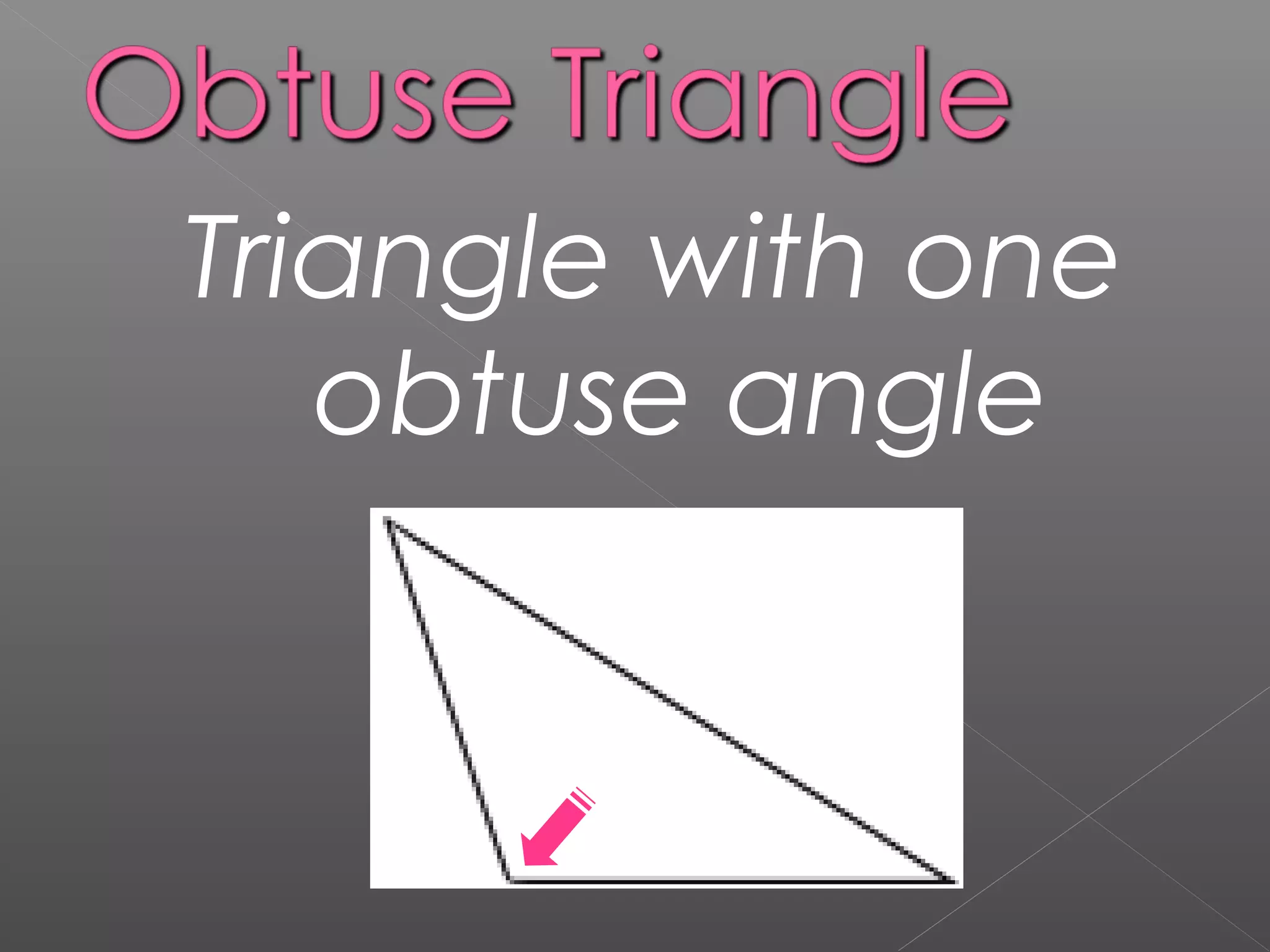
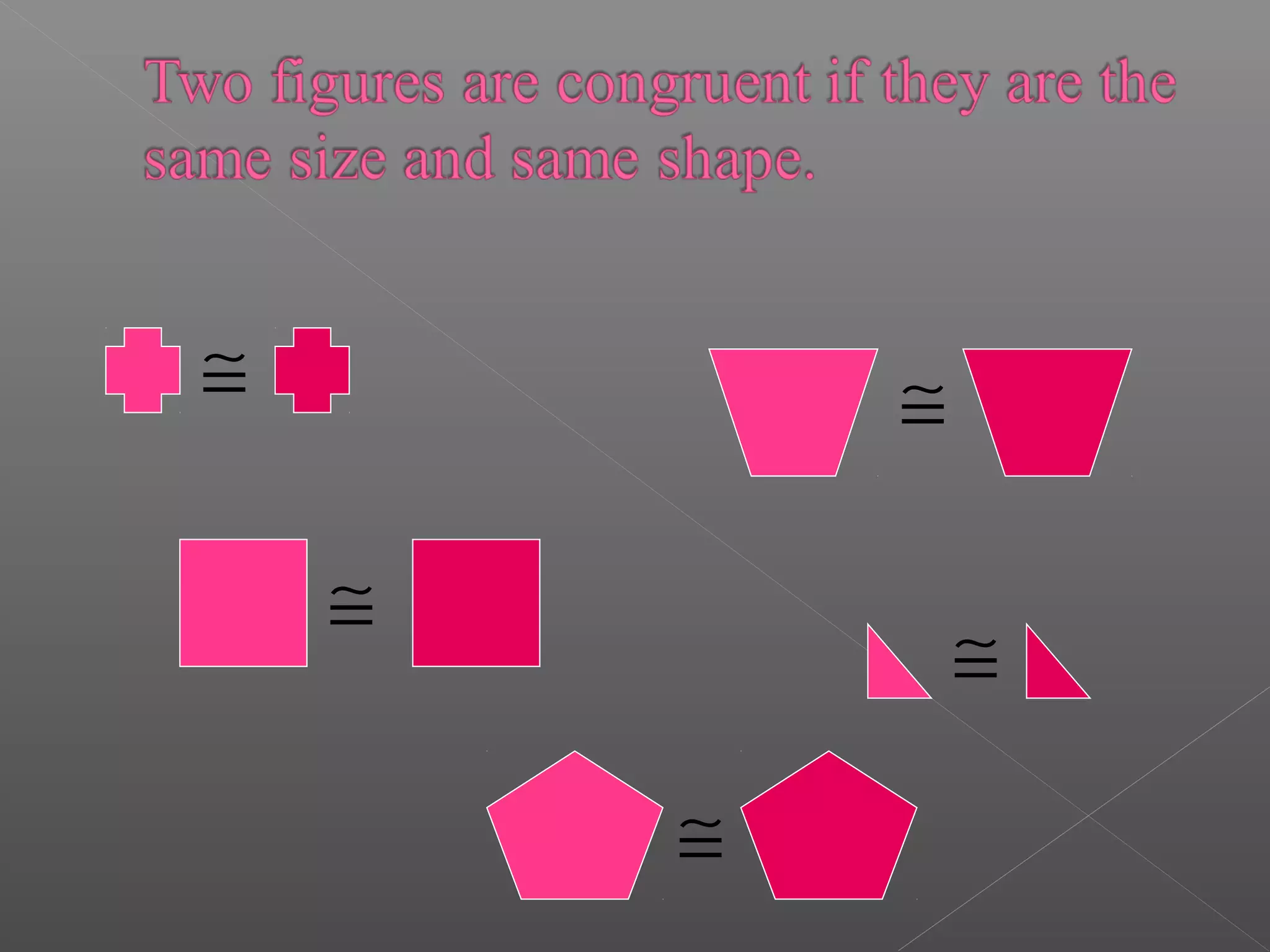
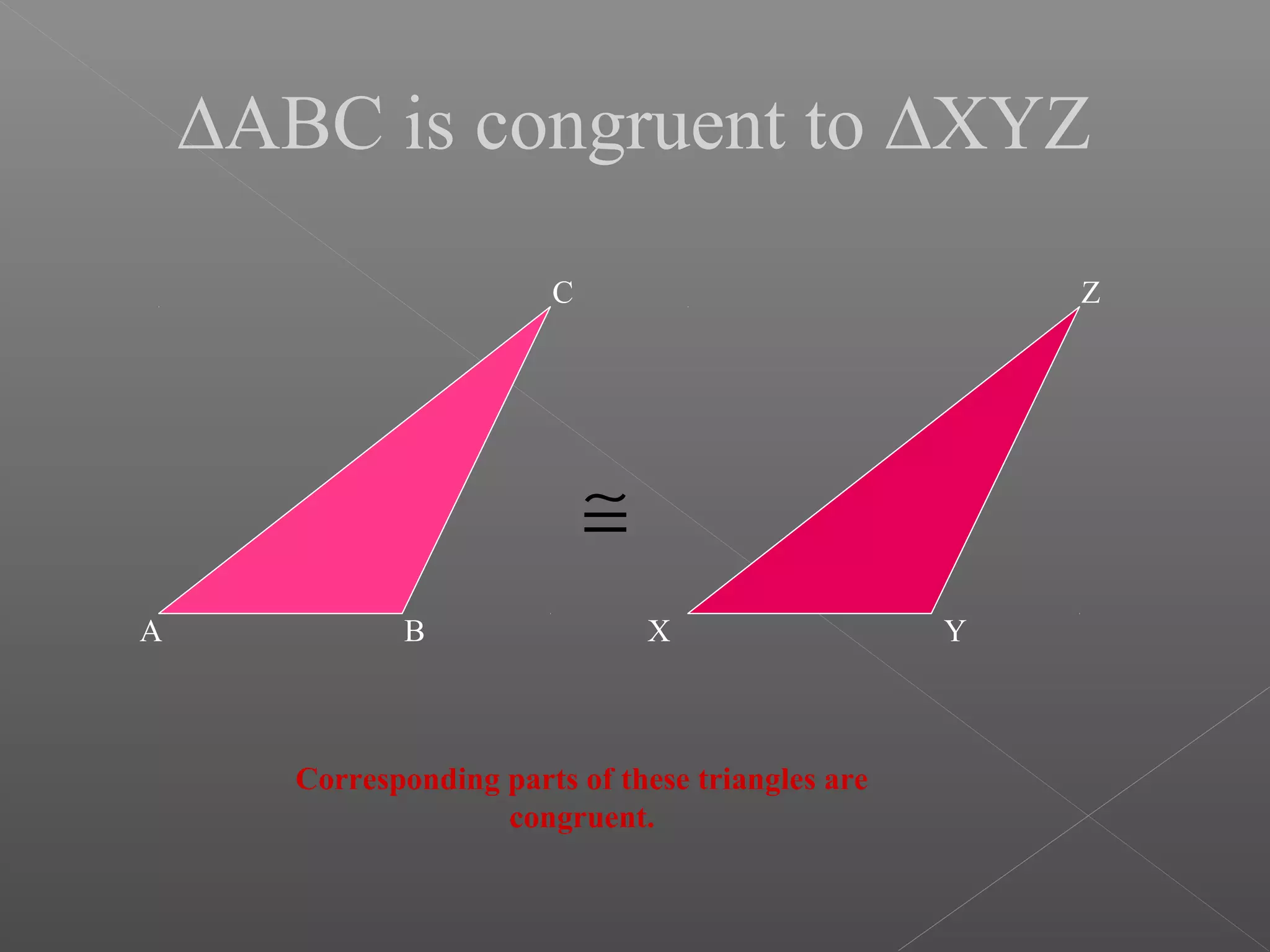
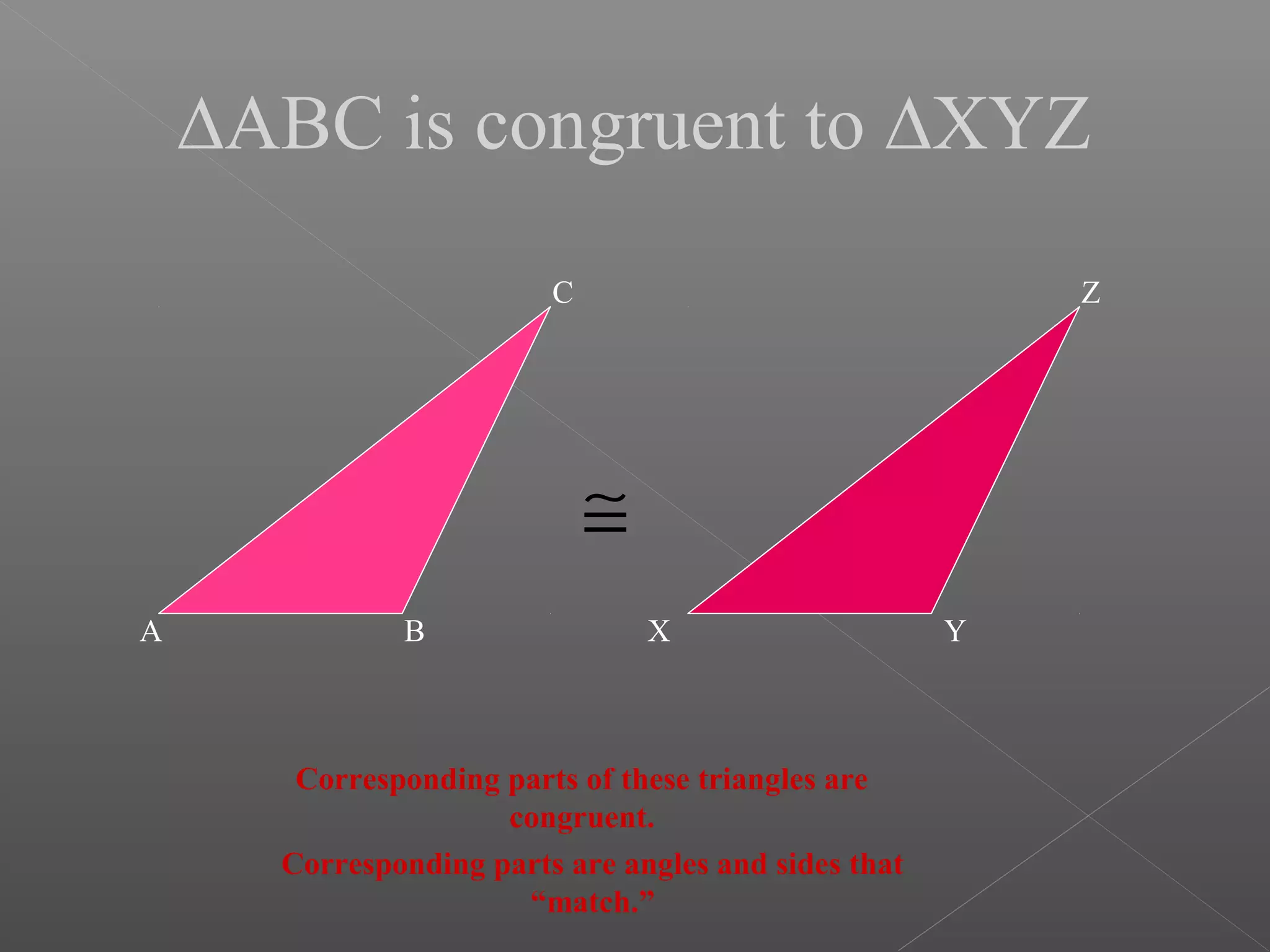
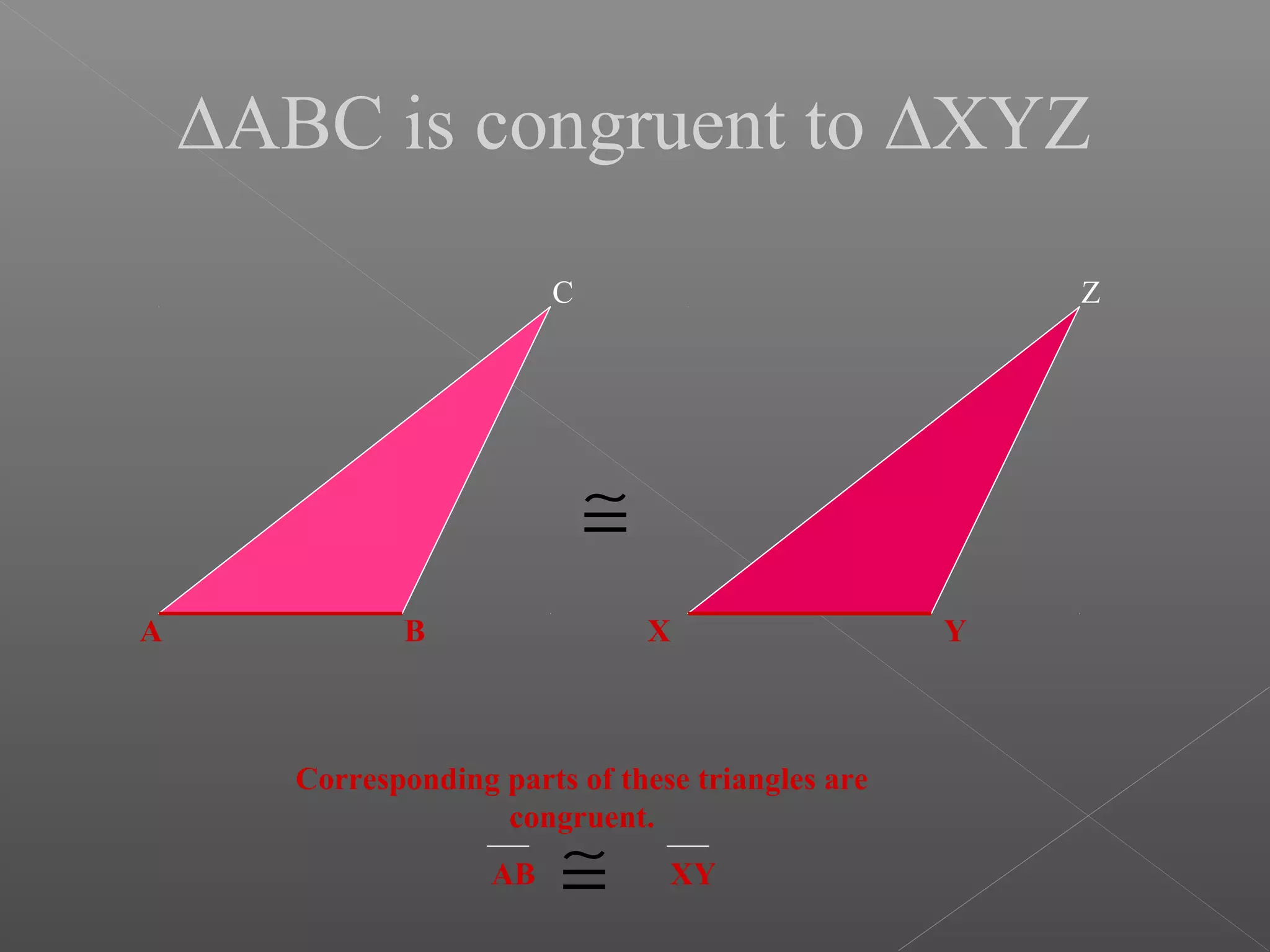
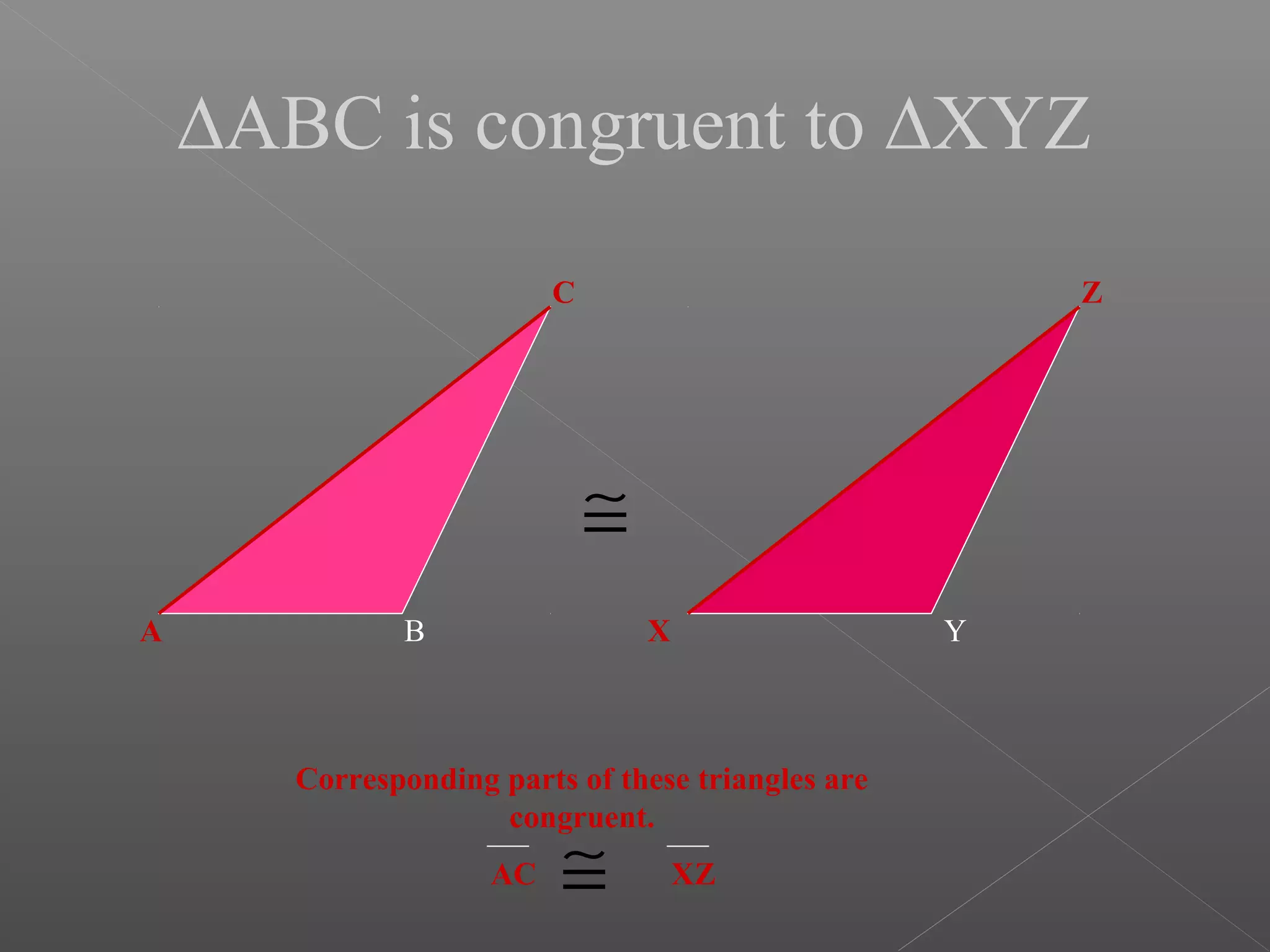
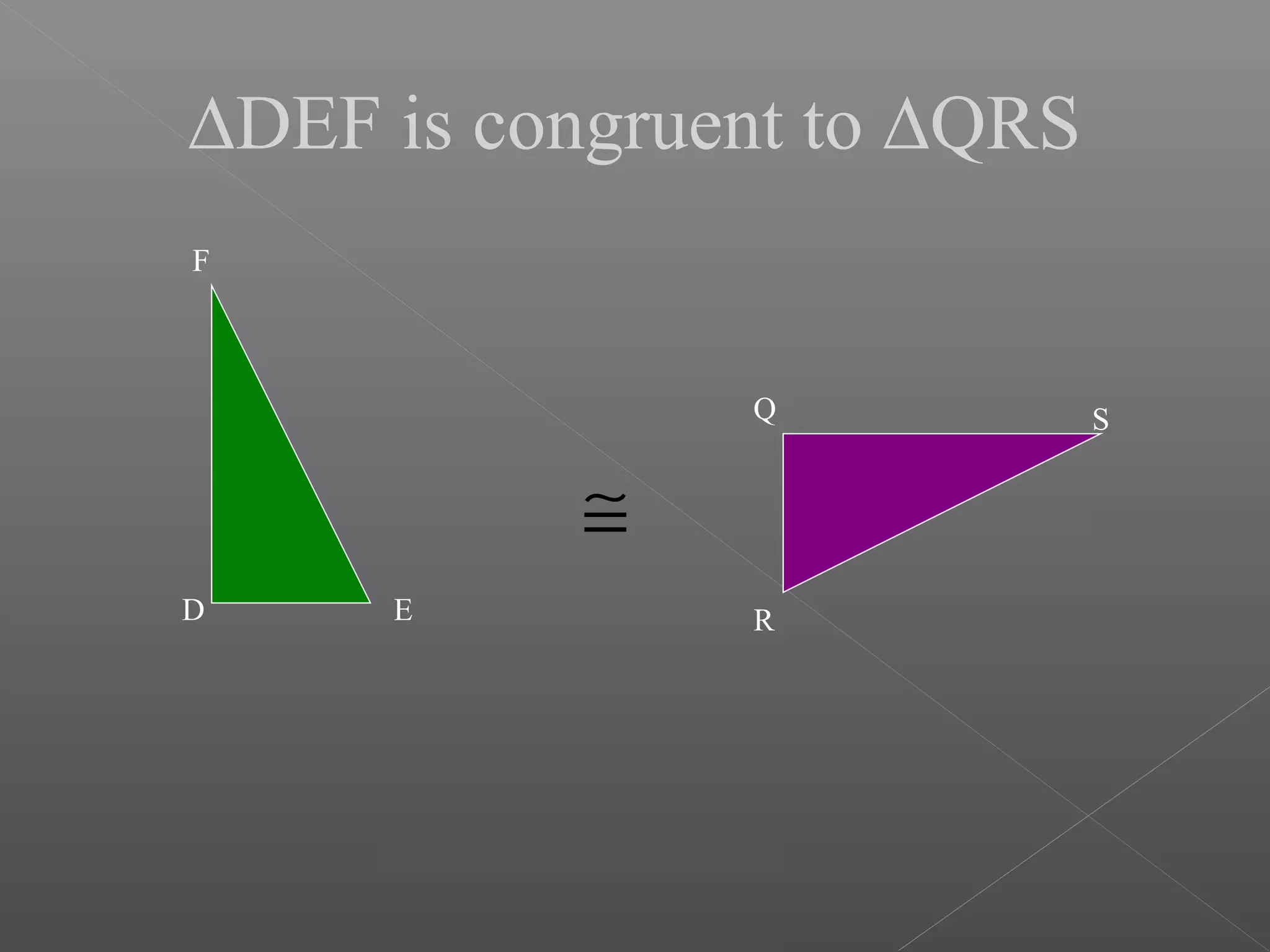
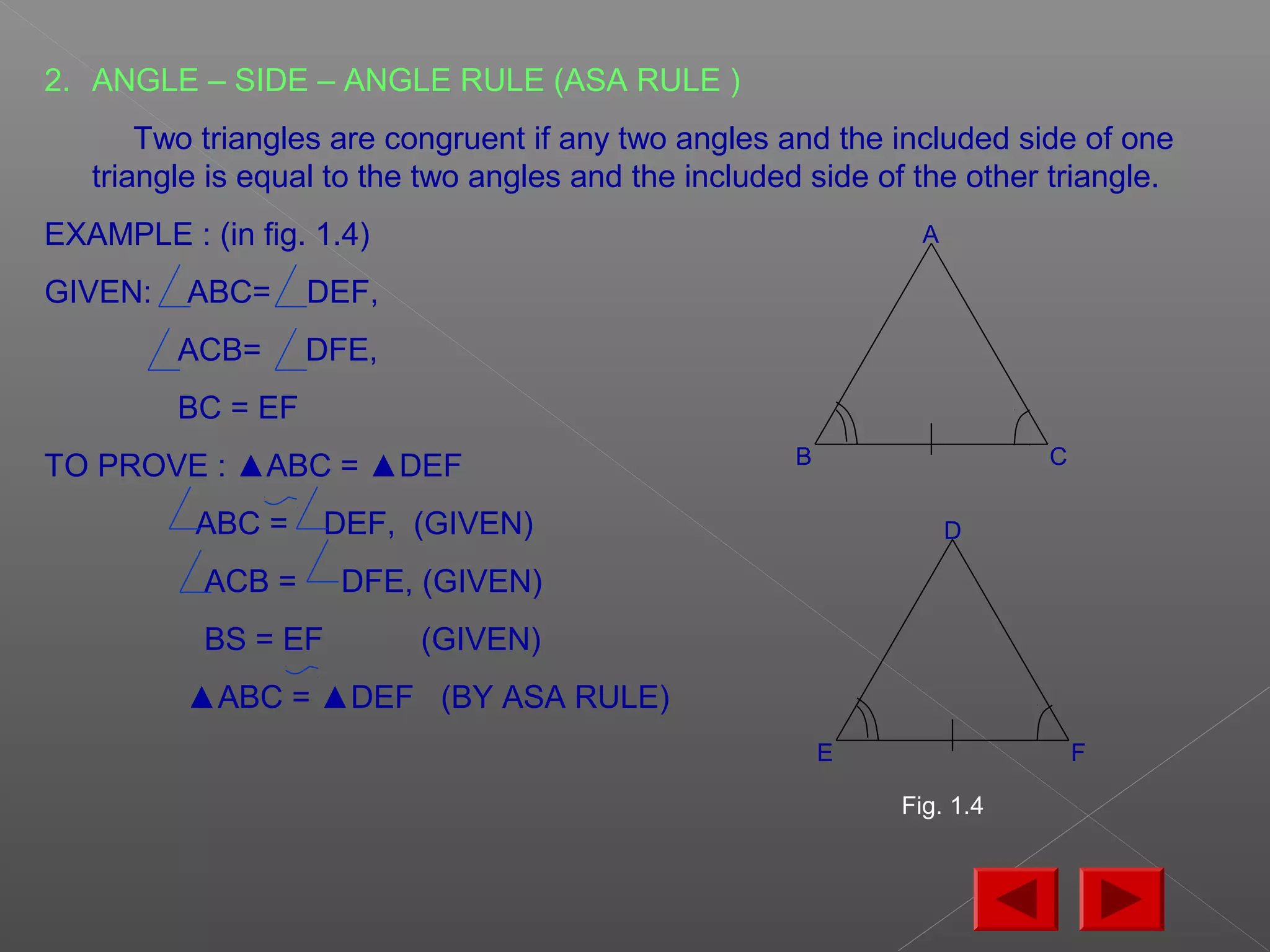
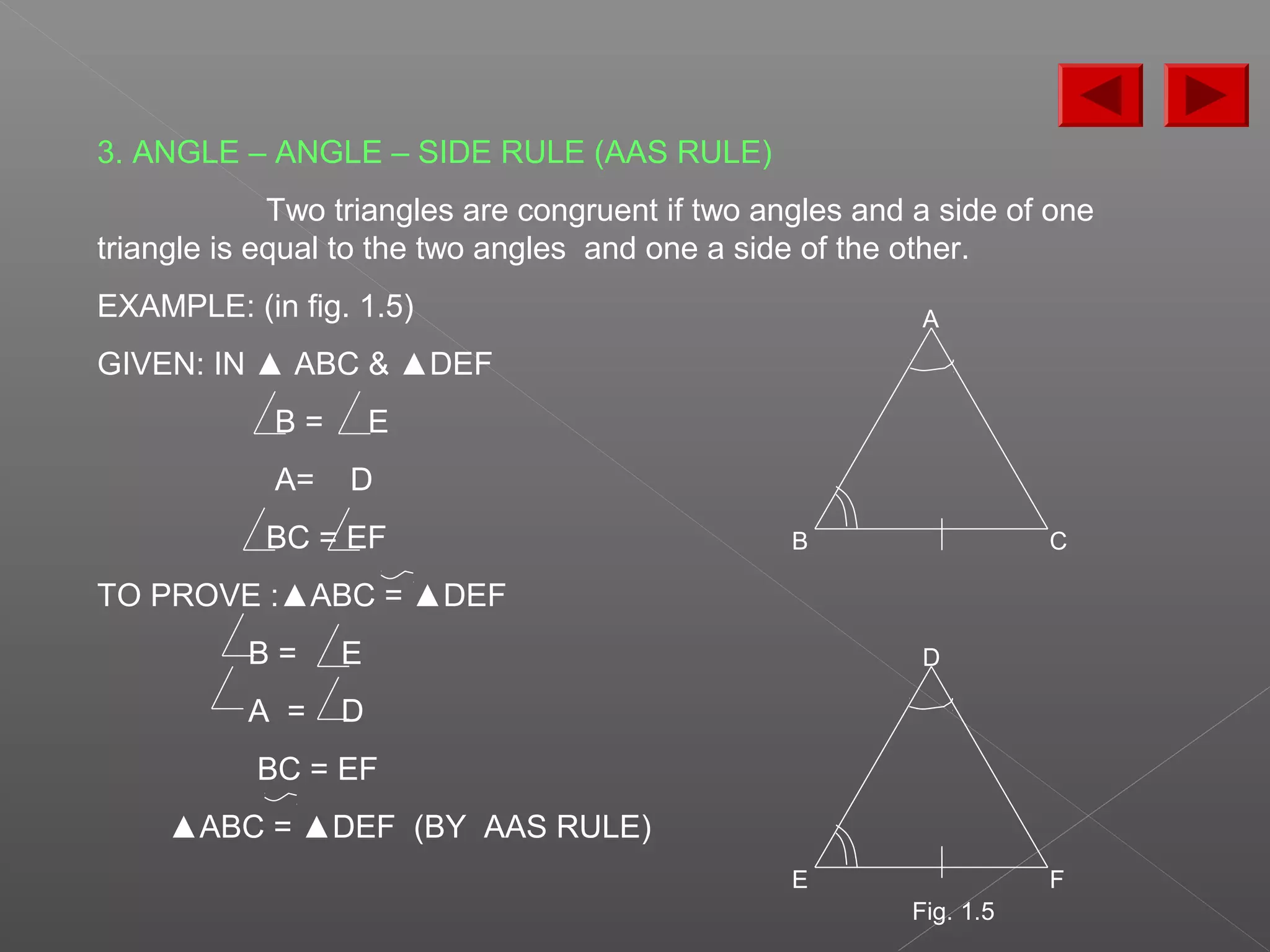
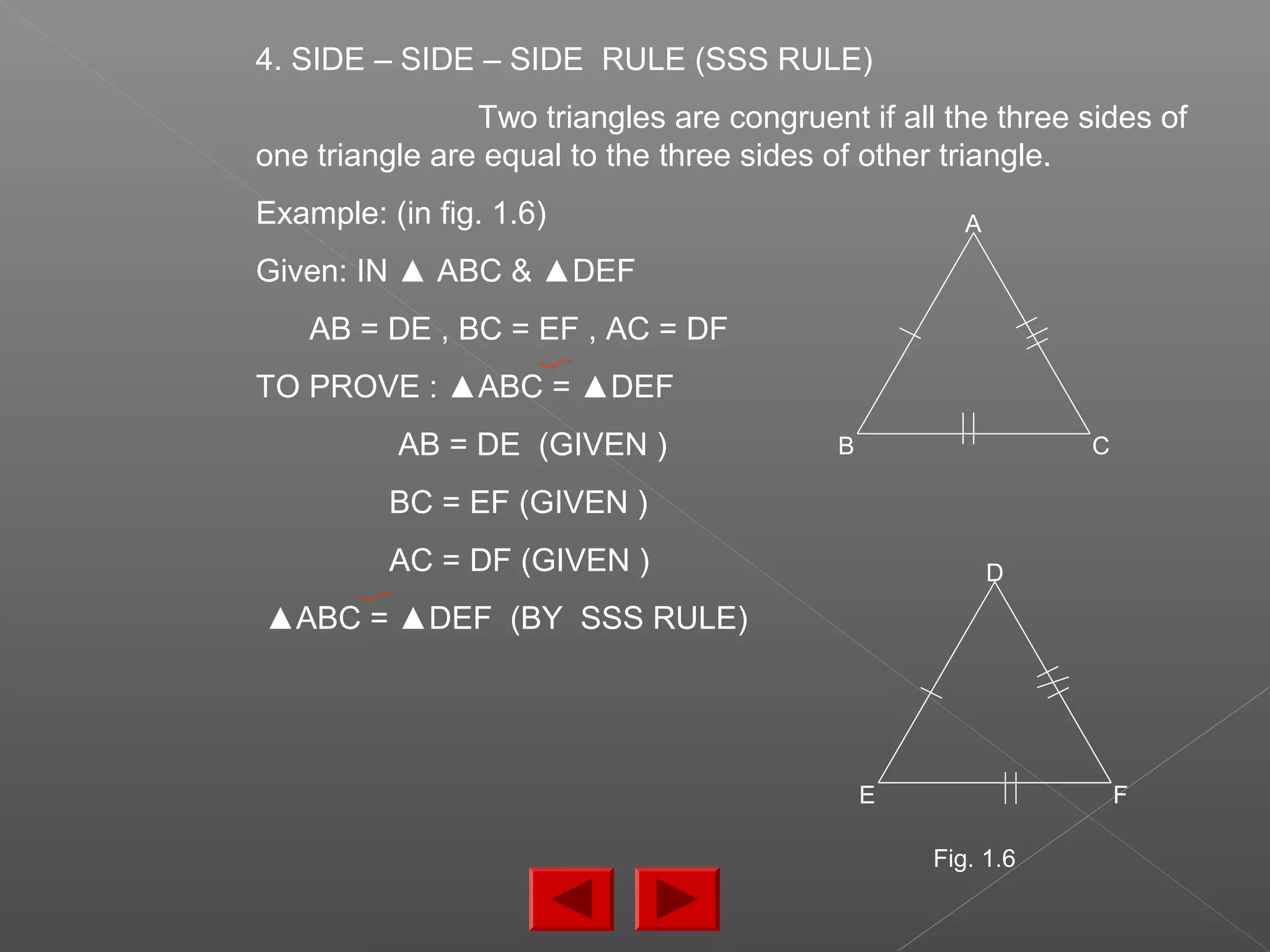
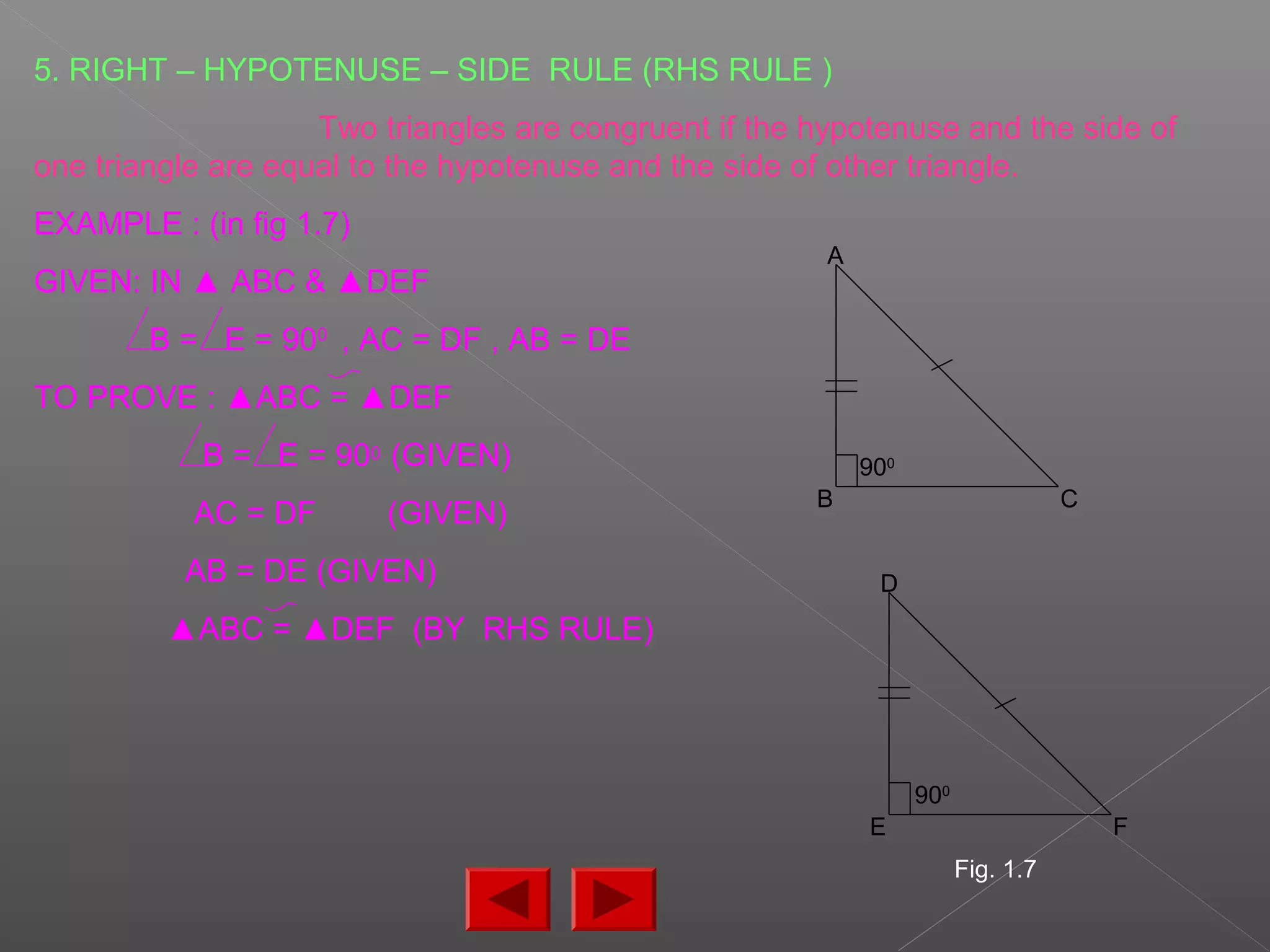
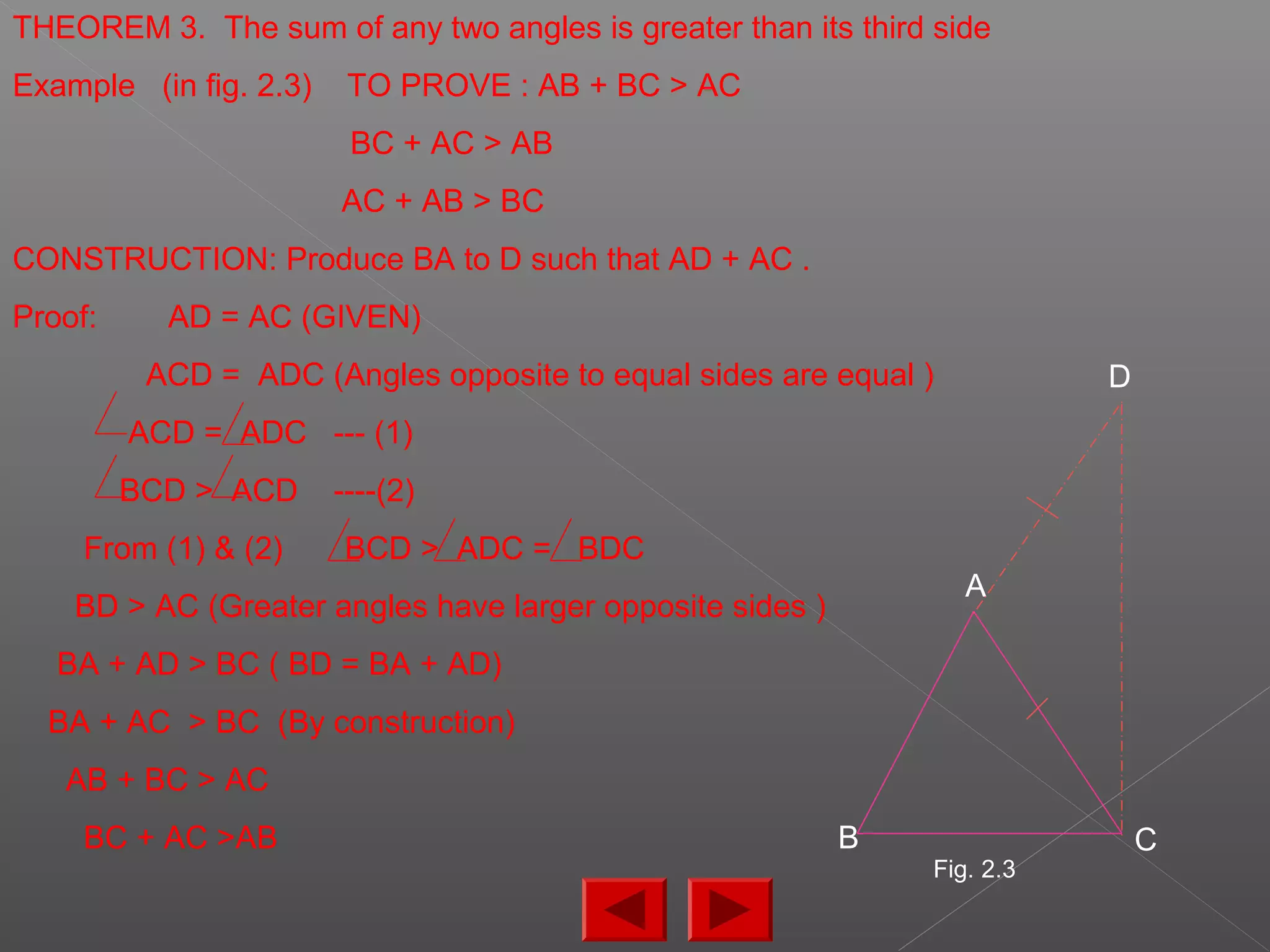
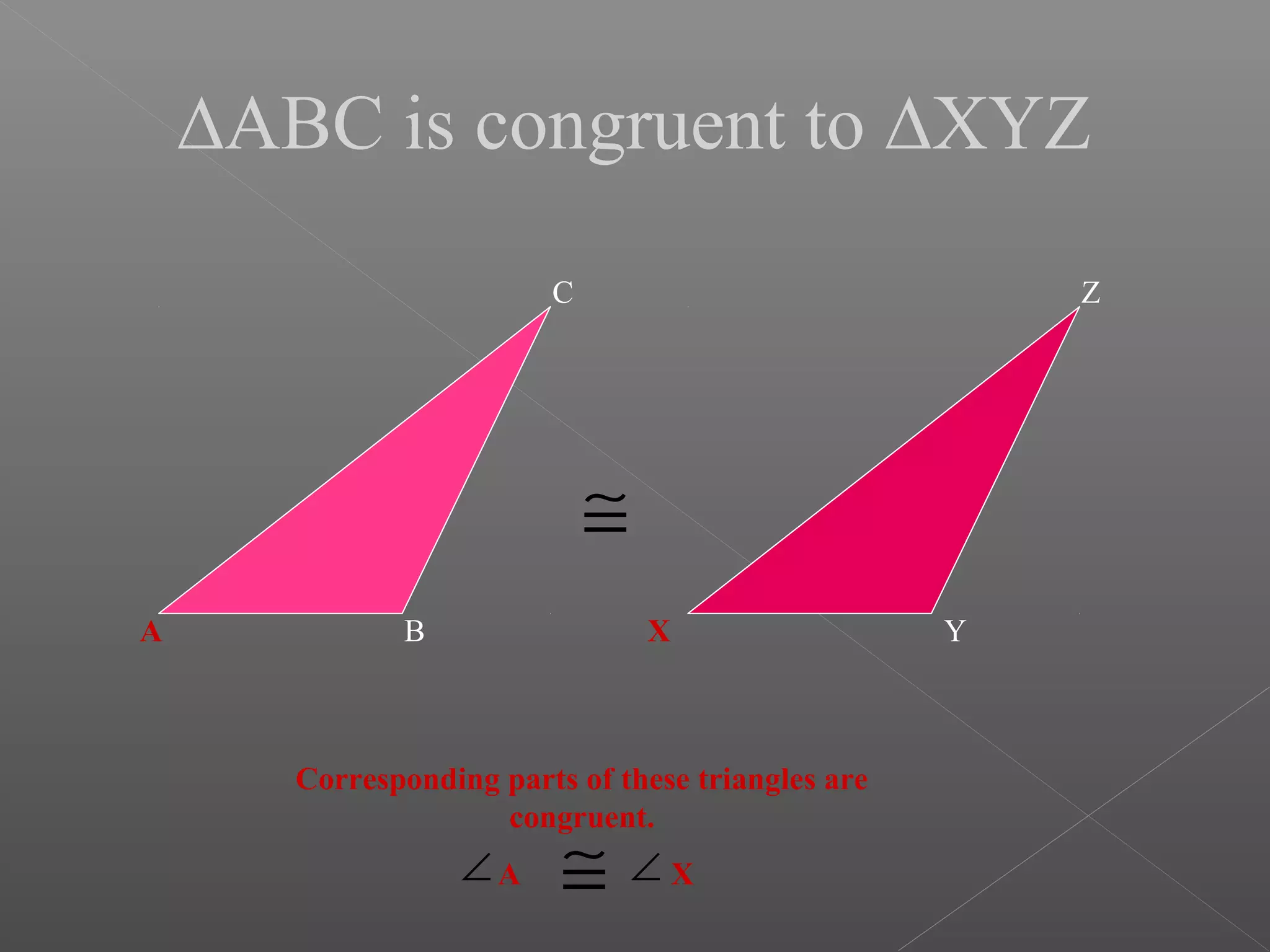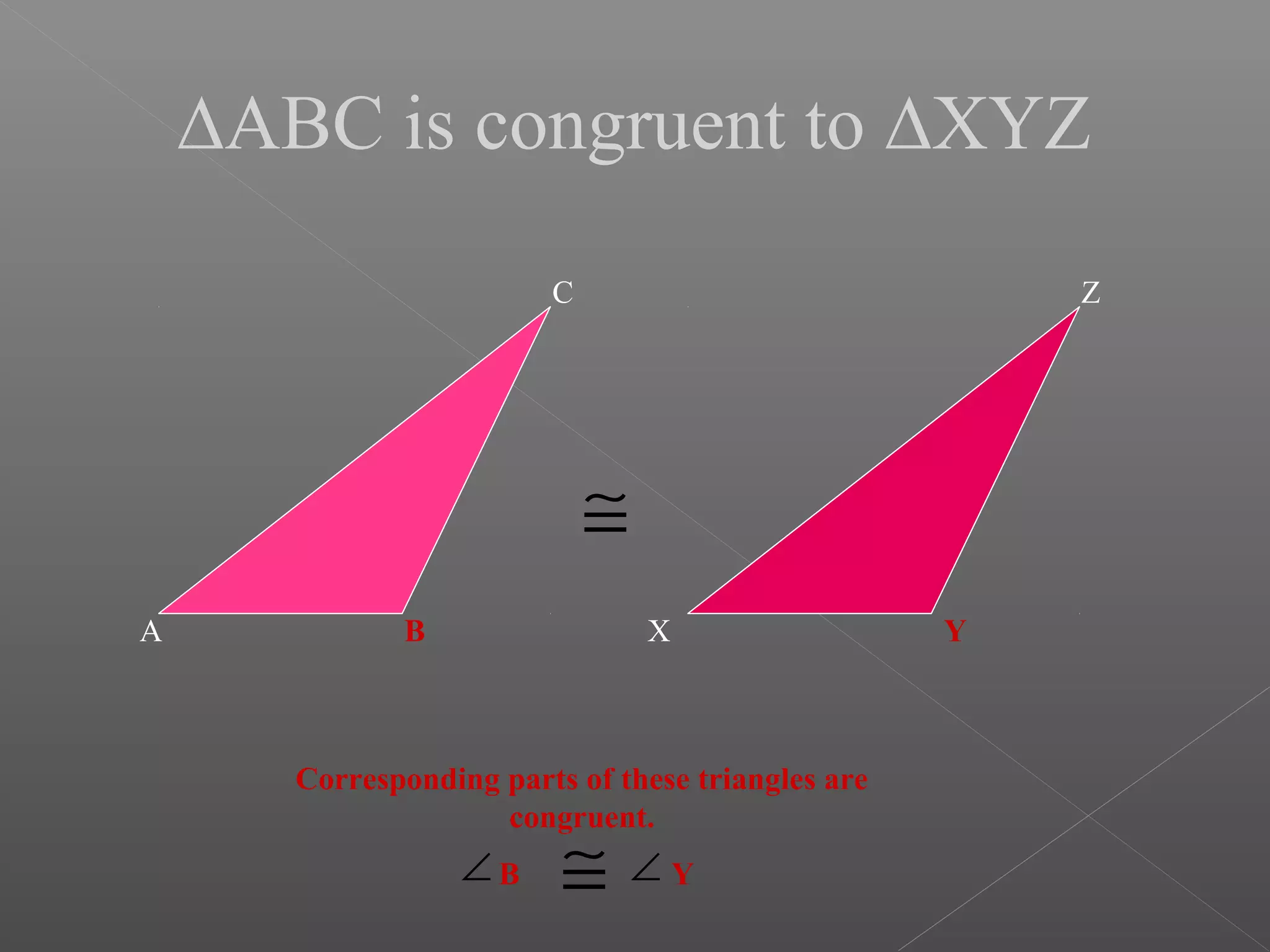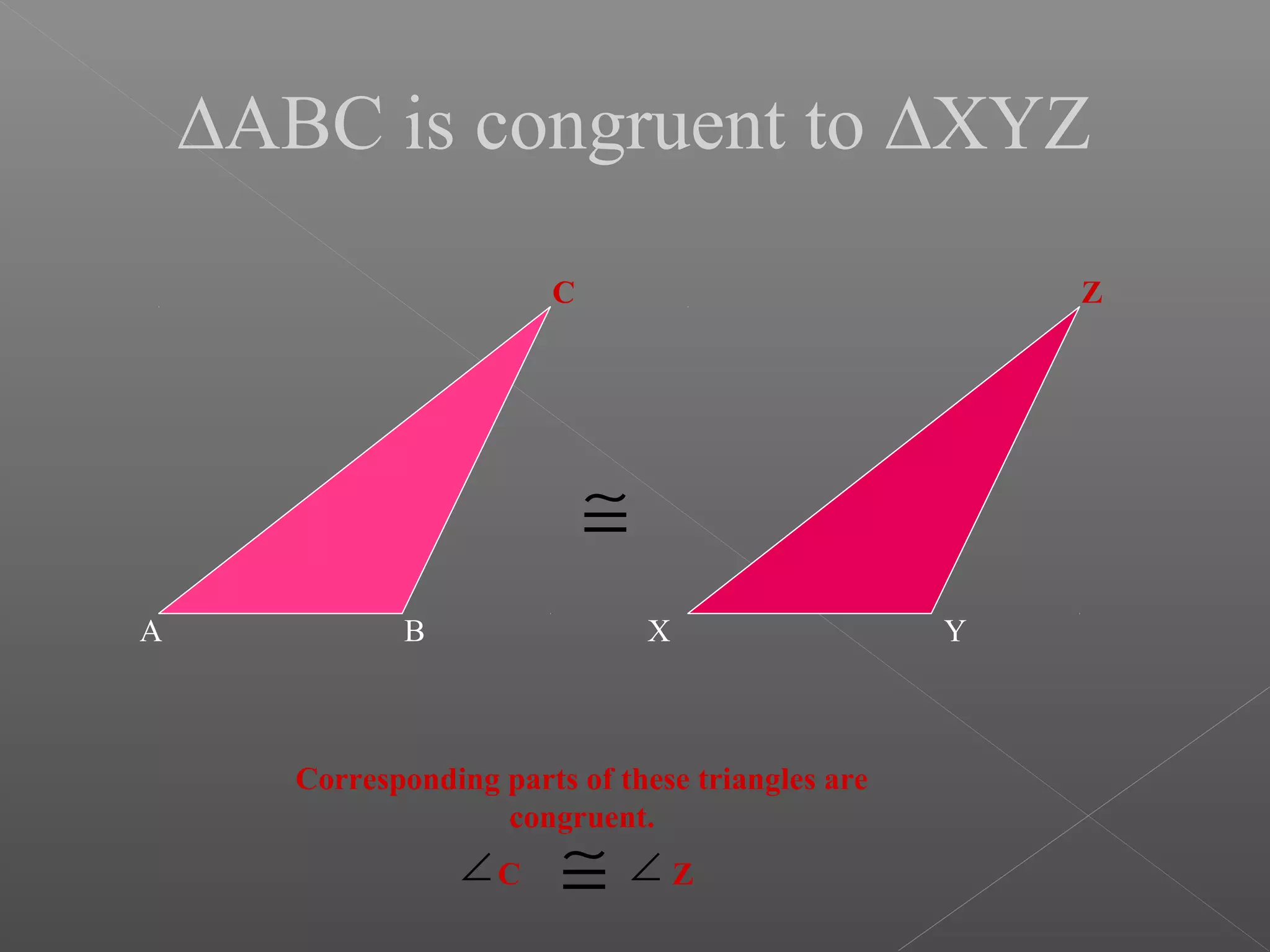The document discusses various properties and theorems related to triangles. It begins by defining different types of triangles based on side lengths and angle measures. It then covers the four congruence rules for triangles: SAS, ASA, AAS, and SSS. The document proceeds to prove several theorems about relationships between sides and angles of triangles, such as opposite sides/angles of isosceles triangles being equal, larger sides having greater opposite angles, and the sum of any two angles being greater than the third side. It concludes by proving that the perpendicular from a point to a line is the shortest segment.

1. Made By – Nitin Chhaperwal
Class 9 R.No-15

2. Can be classified by
the number of
congruent sides

3. Has no congruent
sides

4. Has at least two
congruent sides

5. Has three congruent
sides

6. Can be classified
by the angle
measures

7. Has one right angle

8. Has three acute
angles

9. Triangle with one
obtuse angle

10. Cut any shape
triangle out of a
sheet of paper

11. Tear off the corners.
Piece them together
by having the corners
touch.

12. The sum of the
angles of a triangle
is 180 degrees

13. Congruence
of Triangles

14. ≅
≅
≅
≅
≅
≅

15. Congruent figures can be rotations of
one another.
≅
≅
≅
≅
≅
≅

16. Congruent figures can be reflections of
one another.
≅
≅
≅
≅
≅

17. ≅
A B
C
X Y
Z

18. ∆ABC is congruent to ∆XYZ
A B
C
X Y
Z
≅
Corresponding parts of these triangles are
congruent.

19. ∆ABC is congruent to ∆XYZ
A B
C
X Y
Z
≅
Corresponding parts of these triangles are
congruent.
Corresponding parts are angles and sides that
“match.”

20. ∆ABC is congruent to ∆XYZ
A B
C
X Y
Z
≅
Corresponding parts of these triangles are
congruent.
A X≅∠ ∠

21. ∆ABC is congruent to ∆XYZ
A B
C
X Y
Z
≅
Corresponding parts of these triangles are
congruent.
B Y≅∠ ∠

22. ∆ABC is congruent to ∆XYZ
A B
C
X Y
Z
≅
Corresponding parts of these triangles are
congruent.
C Z≅∠ ∠

23. ∆ABC is congruent to ∆XYZ
A B
C
X Y
Z
≅
Corresponding parts of these triangles are
congruent.
AB XY≅

24. ∆ABC is congruent to ∆XYZ
A B
C
X Y
Z
≅
Corresponding parts of these triangles are
congruent.
BC YZ≅

25. ∆ABC is congruent to ∆XYZ
A B
C
X Y
Z
≅
Corresponding parts of these triangles are
congruent.
AC XZ≅

26. ∆DEF is congruent to ∆QRS
D E
F
≅
Q
R
S

27. ∆DEF is congruent to ∆QRS
D E
F
Q
R
S
≅
Corresponding parts of these triangles are
congruent.

28. ∆DEF is congruent to ∆QRS
D E
F
Q
R
S
≅
Corresponding parts of these triangles are
congruent.
D Q≅∠ ∠

29. ∆DEF is congruent to ∆QRS
D E
F
Q
R
S
≅
Corresponding parts of these triangles are
congruent.
E R≅∠ ∠

30. ∆DEF is congruent to ∆QRS
D E
F
Q
R
S
≅
Corresponding parts of these triangles are
congruent.
F S≅∠ ∠

31. ∆DEF is congruent to ∆QRS
D E
F
Q
R
S
≅
Corresponding parts of these triangles are
congruent.
DE QR≅

32. ∆DEF is congruent to ∆QRS
D E
F
Q
R
S
≅
Corresponding parts of these triangles are
congruent.
DF QS≅

33. ∆DEF is congruent to ∆QRS
D E
F
Q
R
S
≅
Corresponding parts of these triangles are
congruent.
FE SR≅

34. 1. SIDE – ANGLE – SIDE RULE (SAS RULE)
Two triangles are congruent if any two sides and the includes angle of
one triangle is equal to the two sides and the included angle of other
triangle.
EXAMPLE :- (in fig 1.3)
GIVEN: AB=DE, BC=EF ,
B= E
SOLUTION: IF AB=DE, BC=EF , B= E then by SAS Rule
▲ABS = ▲DEF
4 cm4 cm
600
600
A
B C
D
FE
Fig. 1.3

35. 2. ANGLE – SIDE – ANGLE RULE (ASA RULE )
Two triangles are congruent if any two angles and the included side of one
triangle is equal to the two angles and the included side of the other triangle.
EXAMPLE : (in fig. 1.4)
GIVEN: ABC= DEF,
ACB= DFE,
BC = EF
TO PROVE : ▲ABC = ▲DEF
ABC = DEF, (GIVEN)
ACB = DFE, (GIVEN)
BS = EF (GIVEN)
▲ABC = ▲DEF (BY ASA RULE)
A
B C
D
E F
Fig. 1.4

36. 3. ANGLE – ANGLE – SIDE RULE (AAS RULE)
Two triangles are congruent if two angles and a side of one
triangle is equal to the two angles and one a side of the other.
EXAMPLE: (in fig. 1.5)
GIVEN: IN ▲ ABC & ▲DEF
B = E
A= D
BC = EF
TO PROVE :▲ABC = ▲DEF
B = E
A = D
BC = EF
▲ABC = ▲DEF (BY AAS RULE)
D
E F
A
B C
Fig. 1.5

37. 4. SIDE – SIDE – SIDE RULE (SSS RULE)
Two triangles are congruent if all the three sides of
one triangle are equal to the three sides of other triangle.
Example: (in fig. 1.6)
Given: IN ▲ ABC & ▲DEF
AB = DE , BC = EF , AC = DF
TO PROVE : ▲ABC = ▲DEF
AB = DE (GIVEN )
BC = EF (GIVEN )
AC = DF (GIVEN )
▲ABC = ▲DEF (BY SSS RULE)
D
E F
A
B C
Fig. 1.6

38. 5. RIGHT – HYPOTENUSE – SIDE RULE (RHS RULE )
Two triangles are congruent if the hypotenuse and the side of
one triangle are equal to the hypotenuse and the side of other triangle.
EXAMPLE : (in fig 1.7)
GIVEN: IN ▲ ABC & ▲DEF
B = E = 900
, AC = DF , AB = DE
TO PROVE : ▲ABC = ▲DEF
B = E = 900 (GIVEN)
AC = DF (GIVEN)
AB = DE (GIVEN)
▲ABC = ▲DEF (BY RHS RULE)
D
E F
A
B C
900
900
Fig. 1.7

39. 1. The angles opposite to equal sides are always equal.
Example: (in fig 1.8)
Given: ▲ABC is an isosceles triangle in which AB = AC
TO PROVE: B = C
CONSTRUCTION : Draw AD bisector of BAC which meets BC at D
PROOF: IN ▲ABC & ▲ACD
AB = AD (GIVEN)
BAD = CAD (GIVEN)
AD = AD (COMMON)
▲ABD = ▲ ACD (BY SAS RULE)
B = C (BY CPCT)
A
B D C
Fig. 1.8

40. 2. The sides opposite to equal angles of a triangle are always equal.
Example : (in fig. 1.9)
Given : ▲ ABC is an isosceles triangle in which B = C
TO PROVE: AB = AC
CONSTRUCTION : Draw AD the bisector of BAC which meets BC at D
Proof : IN ▲ ABD & ▲ ACD
B = C (GIVEN)
AD = AD (GIVEN)
BAD = CAD (GIVEN)
▲ ABD = ▲ ACD (BY ASA RULE)
AB = AC (BY CPCT)
A
B D C
Fig. 1.9

41. When two quantities are unequal then on comparing
these quantities we obtain a relation between their
measures called “ inequality “ relation.

42. Theorem 1 . If two sides of a triangle are unequal the larger side has the
greater angle opposite to it. Example: (in fig. 2.1)
Given : IN ▲ABC , AB>AC
TO PROVE : C = B
Draw a line segment CD from vertex such that AC = AD
Proof : IN ▲ACD , AC = AD
ACD = ADC --- (1)
But ADC is an exterior angle of ▲BDC
ADC > B --- (2)
From (1) &(2)
ACD > B --- (3)
ACB > ACD ---4
From (3) & (4)
ACB > ACD > B , ACB > B ,
C > B
A
B
D
C
Fig. 2.1

43. THEOREM 2. In a triangle the greater angle has a large side opposite to it
Example: (in fig. 2.2)
Given: IN ▲ ABC B > C
TO PROVE : AC > AB
PROOF : We have the three possibility for sides AB and AC of ▲ABC
(i) AC = AB
If AC = AB then opposite angles of the equal sides are equal than
B = C
AC ≠ AB
(ii) If AC < AB
We know that larger side has greater angles opposite to it.
AC < AB , C > B
AC is not greater then AB
(iii) If AC > AB
We have left only this possibility AC > AB
A
CB
Fig. 2.2

44. THEOREM 3. The sum of any two angles is greater than its third side
Example (in fig. 2.3) TO PROVE : AB + BC > AC
BC + AC > AB
AC + AB > BC
CONSTRUCTION: Produce BA to D such that AD + AC .
Proof: AD = AC (GIVEN)
ACD = ADC (Angles opposite to equal sides are equal )
ACD = ADC --- (1)
BCD > ACD ----(2)
From (1) & (2) BCD > ADC = BDC
BD > AC (Greater angles have larger opposite sides )
BA + AD > BC ( BD = BA + AD)
BA + AC > BC (By construction)
AB + BC > AC
BC + AC >AB
A
CB
D
Fig. 2.3

45. THEOREM 4. Of all the line segments that can be drawn to a given line from an external
point , the perpendicular line segment is the shortest.
Example: (in fig 2.4)
Given : A line AB and an external point. Join CD and draw CE AB
TO PROVE CE < CD
PROOF : IN ▲CED, CED = 900
THEN CDE < CED
CD < CE ( Greater angles have larger side opposite to them. )
B
A
C
ED Fig. 2.4