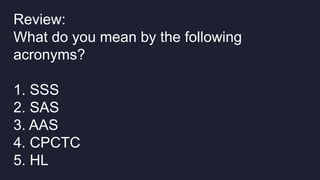
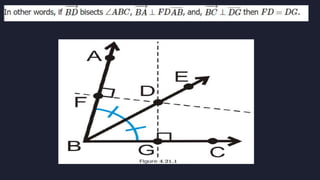
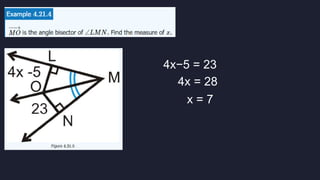
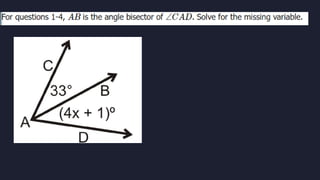
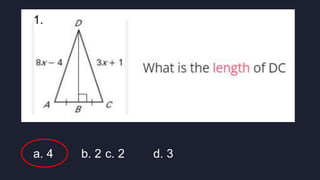
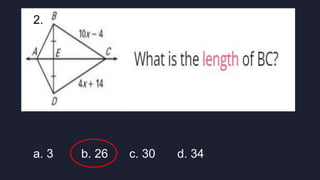
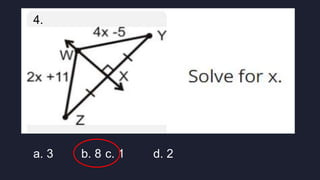
This document discusses using triangle congruence and angle bisectors to construct perpendicular lines. It defines an angle bisector as a line that cuts an angle exactly in half and states that any point on an angle bisector is equidistant from the sides of the angle, according to the Angle Bisector Theorem. The document also reviews triangle congruence theorems and solving simple equations before asking multiple choice questions to test understanding.

1. Applying Triangle Congruence to
Construct Perpendicular Lines
and Angle Bisector

2. Objectives: At the end of the lesson, 75 % of
the students will be able to:
1. Define angle bisector.
2. Draw an angle bisector equidistant from
the sides of the angle.
3. Appreciate congruences and exact
measurements of angles and lines.

4. Review:
What do you mean by the following
acronyms?
1. SSS
2. SAS
3. AAS
4. CPCTC
5. HL

5. Unequal distribution of wealth

6. Angle Bisector Theorem
An angle bisector cuts an angle exactly in
half. One important property of angle
bisectors is that if a point is on the bisector of
an angle, then the point is equidistant from
the sides of the angle. This is called the
Angle Bisector Theorem.

8. Angle Bisector Theorem Converse: If a point is in the
interior of an angle and equidistant from the sides, then
it lies on the bisector of that angle.

9. 4x−5 = 23
4x = 28
x = 7

10. x + 7 = 2(3x – 4)
x + 7 = 6x - 8
15x = 5
x = 3

12. a. 4 b. 2 c. 2 d. 3
1.

13. a. 3 b. 26 c. 30 d. 34
2.

14. a. 2 b. 4 c. 6 d. 8
3.

15. a. 3 b. 8 c. 1 d. 2
4.

16. What is the name of the triangle and its perpendicular
bisector?
The point at which the perpendicular bisectors of a
triangle meet are known as the circumcenter of the
triangle and it is equidistant from all the vertices.