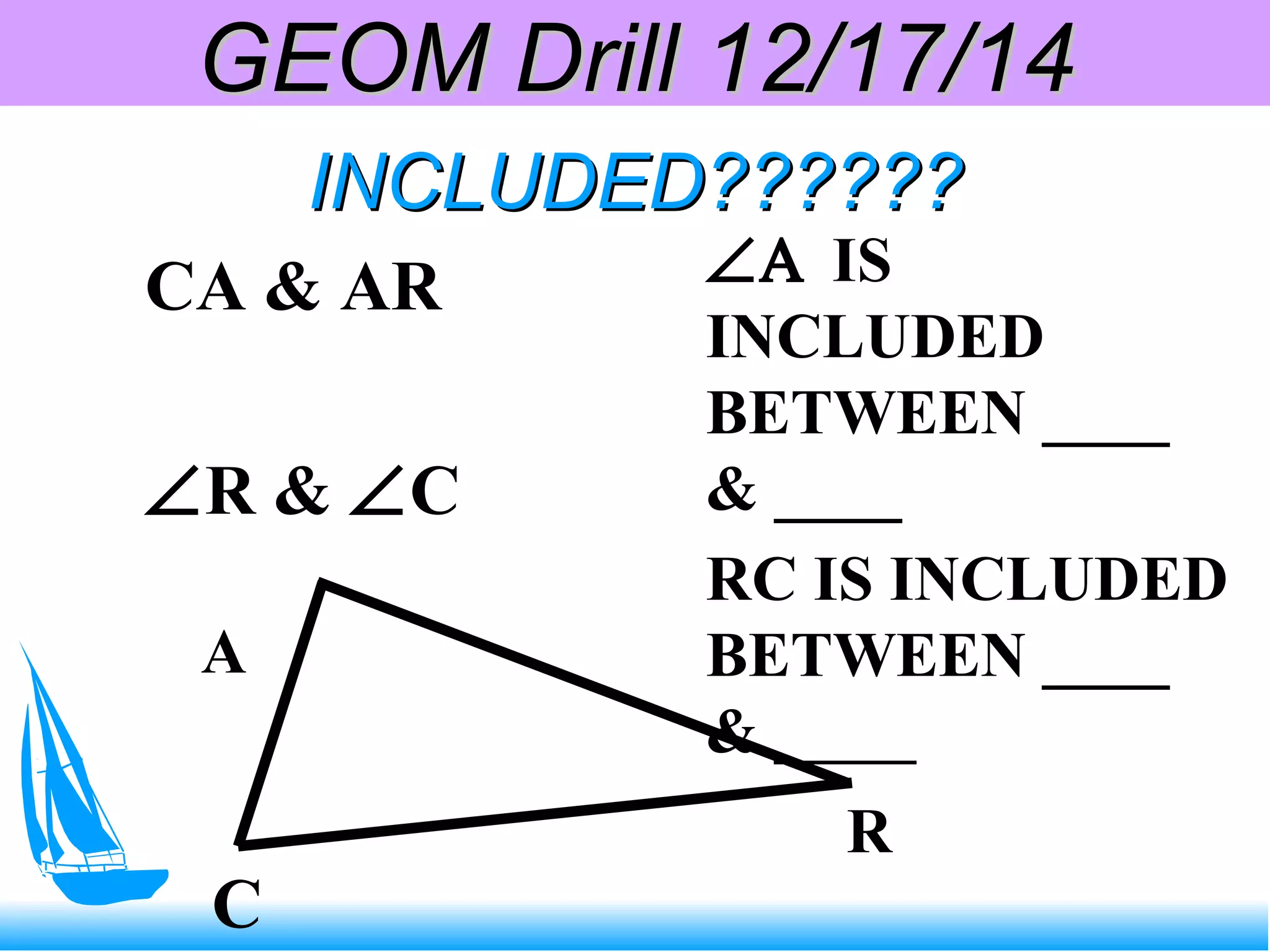
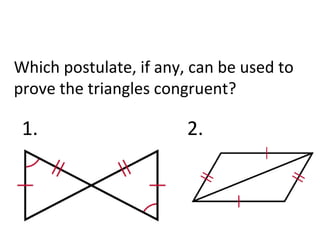
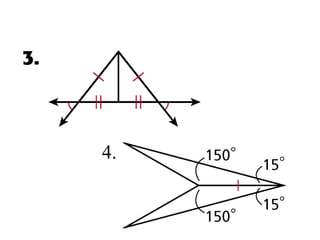
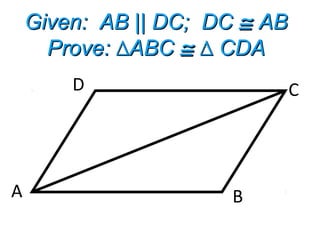
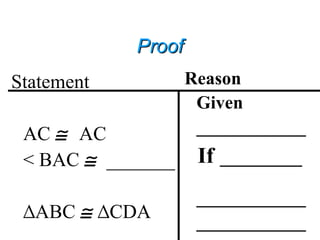
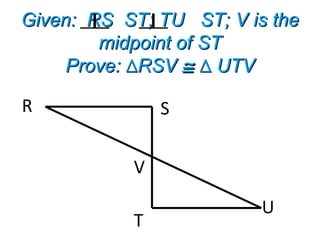
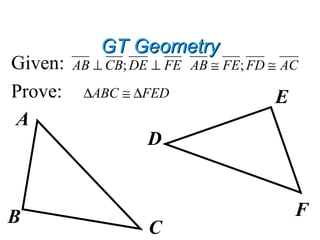
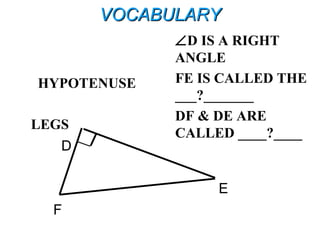
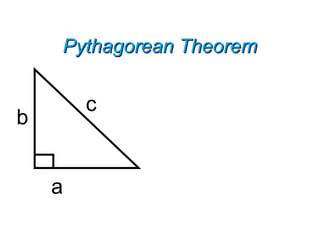
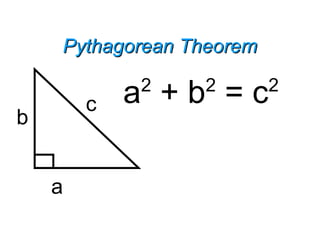
This document contains information about proving triangles congruent using various postulates and theorems of geometry including: - SSS (side-side-side) postulate - SAS (side-angle-side) postulate - ASA (angle-side-angle) postulate - AAS (angle-angle-side) theorem - Hypotenuse-Leg theorem It also defines key terms like hypotenuse and legs of a right triangle and presents the Pythagorean theorem.

1. INCLUDED??????INCLUDED??????
CA & AR
∠R & ∠C
∠Α IS
INCLUDED
BETWEEN ____
& ____
RC IS INCLUDED
BETWEEN ____
& _____
C
A
R
GEOM Drill 12/17/14GEOM Drill 12/17/14

2. How do we know twoHow do we know two
figures are congruent?figures are congruent?
If all corresponding sides
and angles are congruent

3. Objective:Objective:
To determine ways to
prove triangles
congruent

4. POSTULATE - SSS POST.POSTULATE - SSS POST.
If three sides of one triangle
are congruent to three sides
of another triangle then the
triangles are congruent.

5. POSTULATE - SAS POST.POSTULATE - SAS POST.
If two sides and the included
angle of one triangle are
congruent to two sides and the
included angle of another
triangle then the triangles are
congruent.

6. POSTULATE - ASA POST.POSTULATE - ASA POST.
If two angles and the included
side of one triangle are
congruent to two angles and the
included side of another triangle
then the triangles are
congruent.

7. To determine if triangles are
congruent, what would you
have to measure?
SSS
SAS
ASA
All sides & all angles.

8. Which postulate, if any, can be used to
prove the triangles congruent?
1. 2.

9. 4.

10. GT Geometry DrillGT Geometry DrillWrite down the name of the figure described.
Only 1 figure. I will keep giving hints
Hint 1 : I am a special polygon
Hint 2: I have three sides
Hint 3: I have an angle that is neither obtuse
or acute
Hint 4: My sides have a special relationship
Right Triangle

11. VOCABULARYVOCABULARY
HYPOTENUSE
LEGS
∠D IS A RIGHT
ANGLE
FE IS CALLED THE
___?_______
DF & DE ARE
CALLED ____?____
F
D
E

12. Geometry ObjectiveGeometry Objective
STW continue to prove
triangle congruent

13. Given: AB || DC; DCGiven: AB || DC; DC ≅≅ ABAB
Prove: ABC∆Prove: ABC∆ ≅≅ CDA∆ CDA∆
D C
A B

14. ProofProof
Statement
AC ≅ AC
< BAC ≅ _______
∆ABC ≅ CDA∆
Reason
Given
____________
If _________
____________
____________

15. Given: RS ST; TU ST; V is theGiven: RS ST; TU ST; V is the
midpoint of STmidpoint of ST
Prove: RSV∆Prove: RSV∆ ≅≅ UTV∆ UTV∆
R S
T
U
V
⊥ ⊥

16. ProofProof
Statement Reason

17. AAS THEOREMAAS THEOREM
If two angles and a non-included
side of one triangle are
congruent to two angles and a
non-included side of another
triangle then the triangles are
congruent.

18. GT GeometryGT Geometry
Given:
Prove:
A
B
C
D
E
F
FEDECBAB ⊥⊥ ; ACFDFEAB ≅≅ ;
FEDABC ∆≅∆

19. Pythagorean TheoremPythagorean Theorem
a
b
c

20. Pythagorean TheoremPythagorean Theorem
a
b
c a2
+ b2
= c2

21. HLTHEOREMHLTHEOREM
If the hypotenuse and a leg of
one right triangle are
congruent to the hypotenuse
and a leg of another right
triangle , then the triangles are
congruent.