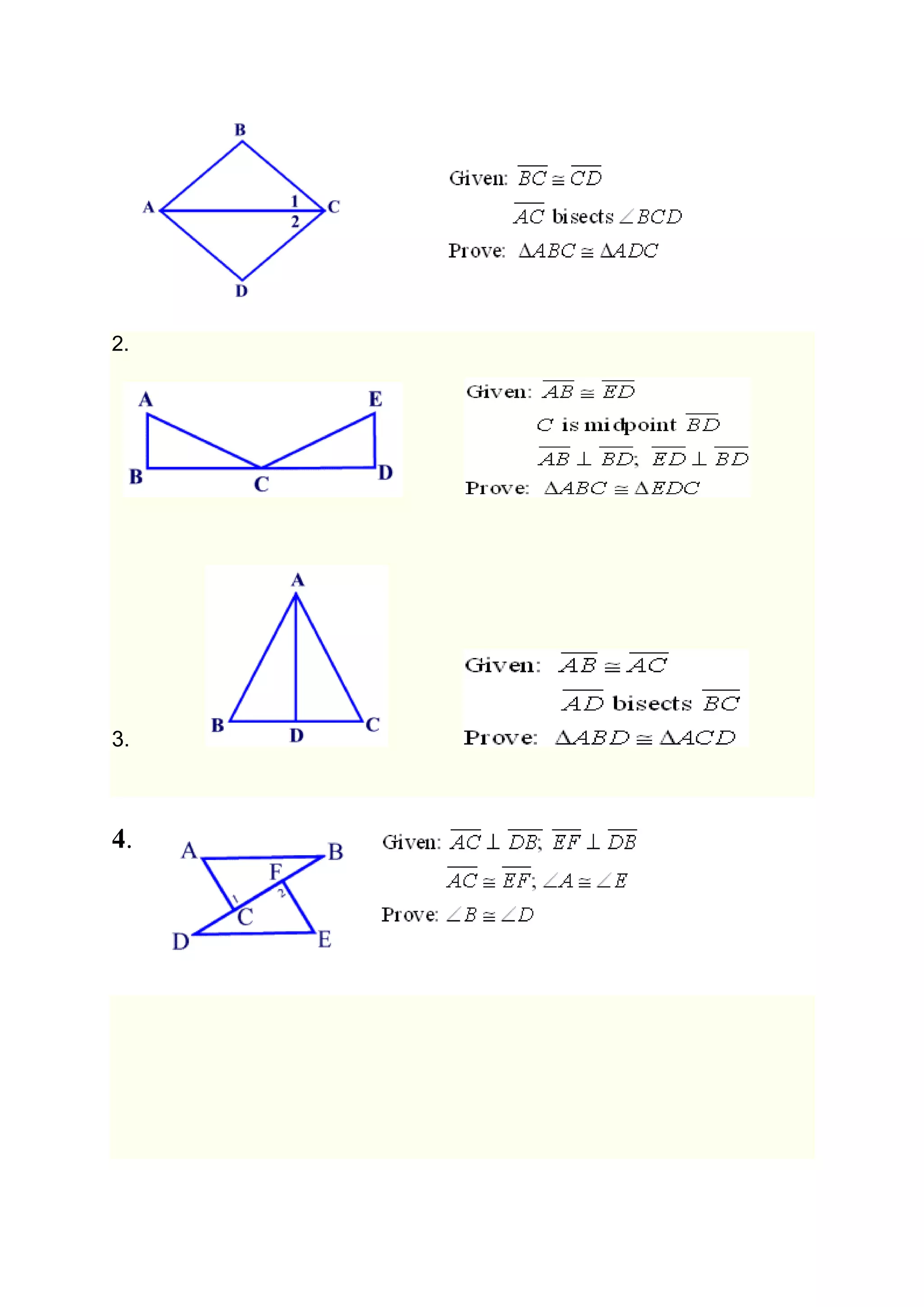
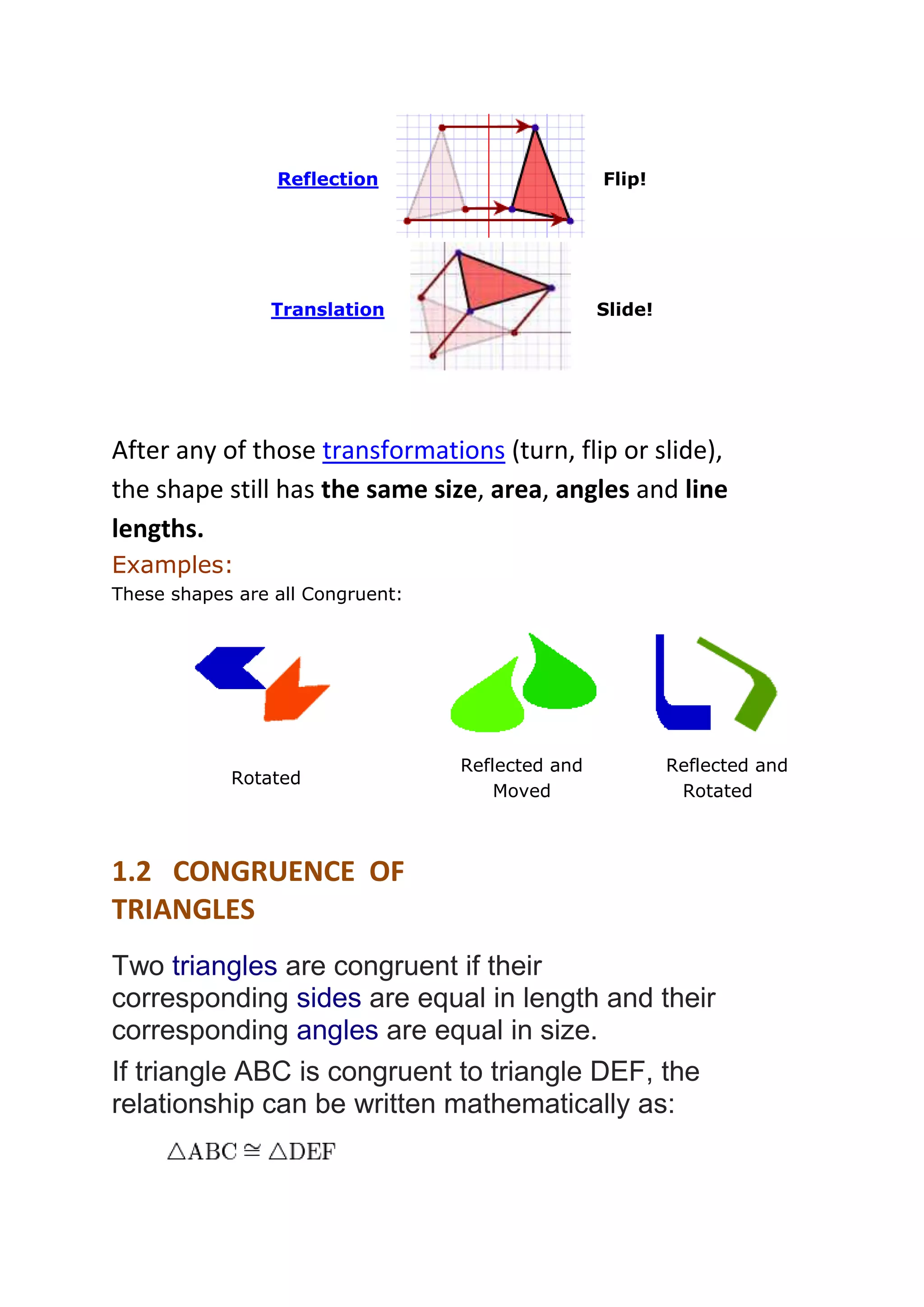
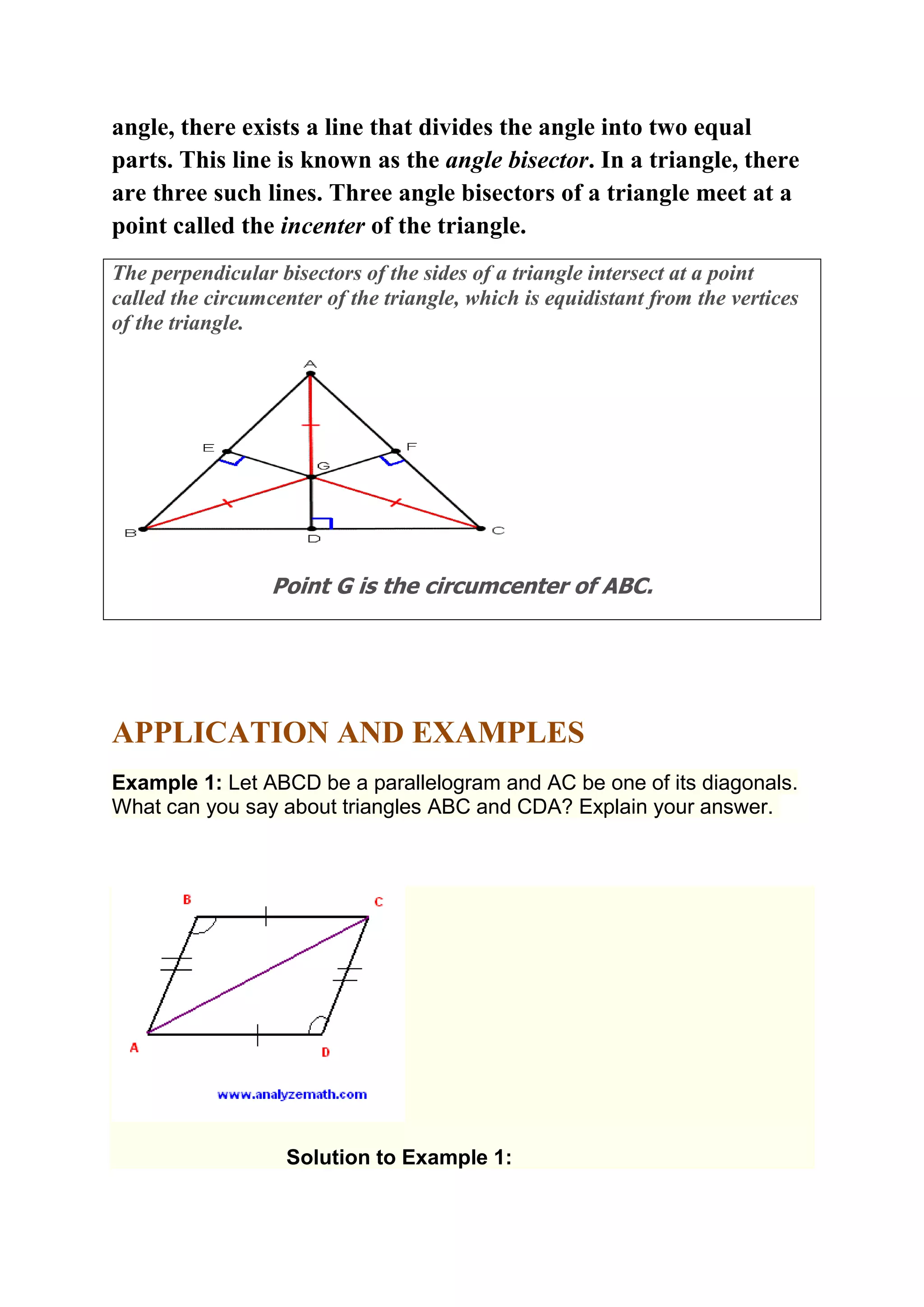
This document provides information about congruent triangles. It defines congruent triangles as two triangles that have the same shape and size, with corresponding sides and angles being equal. It describes several triangle congruence theorems including SSS, SAS, ASA, AAS, and RHS, which establish that triangles are congruent if certain combinations of sides and/or angles are equal. It also discusses isosceles triangles, angle bisectors, and provides examples applying the congruence theorems to prove triangles are congruent or not.

1. MATHEMATICS
Standard -8
By
Shelin Elizabeth Varghese
B.Ed Mathematics
Reg No:13304013

2. CONTENTS
 CONGRUENT TRIANGLES
 CONGRUENCE OF TRIANGLES
 SSS CONGRUENCE
 SAS CONGRUENCE
 ASA CONGRUENCE
 AAS CONGRUENCE
 RHS CONGRUENCE
 ISOSCELES TRIANGLE
 BISECTORS
 APPLICATION AND EXAMPLES

3.  CONGRUENT TRIANGLES
1.1 CONCEPT OF CONGRUENCE
In our daily life you observe various figures and objects. These
figures or objects can be categorised in terms of their shapes and sizes
in the following manner.
(i) Figures, which have different shapes and sizes as shown in Fig.
11.1
(ii) Objects, which have same shapes but different sizes as shown in
Fig. 11.2

4. (iii) Two one-rupee coins.
.
Two figures, which have the same shape and same size are called
congruent figures and this property is called congruence.
What is "Congruent" ... ?
Equal in size and shape. Two objects are congruent if they
have the same dimensions and shape.
If one shape can become another using Turns, Flips and/or
Slides, then the shapes are Congruent.
Rotation
Turn!

5. Reflection
Flip!
Translation
Slide!
After any of those transformations (turn, flip or slide),
the shape still has the same size, area, angles and line
lengths.
Examples:
These shapes are all Congruent:
Rotated
Reflected and
Moved
Reflected and
Rotated
1.2 CONGRUENCE OF
TRIANGLES
Two triangles are congruent if their
corresponding sides are equal in length and their
corresponding angles are equal in size.
If triangle ABC is congruent to triangle DEF, the
relationship can be written mathematically as:

6. Refresh your mind
CONGRUENT TRIANGLES - ENGLISH - Simple paper folding proof..avi
1.3 SSS CONGRUENCE
SSS (Side-Side-Side): If three pairs of sides of two triangles are equal in
length, then the triangles are congruent.
For example:
is
congruent
to:
and
because they all have exactly the same sides.
But:
is NOT congruent to:
because the two triangles do not have exactly the same sides.
1.4 SAS CONGRUENCE
SAS (Side-Angle-Side): If two pairs of sides of two triangles are equal
in length, and the included angles are equal in measurement, then
the triangles are congruent.
For example:

7. is congruent to:
1.5 ASA CONGRUENCE
ASA (Angle-Side-Angle): If two pairs of angles of two
triangles are equal in measurement, and the included
sides are equal in length, then the triangles are congruent.
For example:
is congruent
to:
1.6 AAS CONGRUENCE
AAS (Angle-Angle-Side): If two pairs of angles of two triangles
are equal in measurement, and a pair of corresponding non-included
sides are equal in length, then the triangles are
congruent.
For example:
is congruent to:

8. 1.7 RHS CONGRUENCE
RHS (Right-angle-Hypotenuse-Side): If two right-angled
triangles have their hypotenuses equal in length, and a pair of
shorter sides are equal in length, then the triangles are
congruent.
For example:
is congruent to:
Refresh your mind!
CONGRUENT TRIANGLES (ANIMATION).avi

9. SSA DOESN’T WORK
AB is the same length as PQ, BC is the same length as QR, and the angle A is the same measure as P. And yet the
triangles are clearly not congruent - they have a different shape and size.
Caution ! Don't Use "AAA" !
AAA means we are given all three angles of a triangle, but no sides.
This is not enough information to decide if two triangles are congruent!
Because the triangles can have the same angles but be different sizes:
is not congruent
to:
 CHECK YOUR PROGRESS
Prove that the points of intersection of the two diagonals of a parallelogram is the
midpoint of both the diagonals.
ISOSCELES TRIANGLE
An isosceles triangle is a triangle that has two sides of

10. equal length. The angles opposite the equal sides are also
equal.
Theorem 1
If a triangle has two sides of equal length, then the angles
opposite to these sides are congruent.
Proof
Let ABC be a triangle with sides AC and BC of
equal length (Figure
1).
We need to prove that angles BAC and ABC are
congruent.
Consider the triangle BAC.
The side AC of the triangle ABC corresponds to
the side BC of the triangle BAC.
The side BC of the triangle ABC corresponds to
the side AC of the triangle BAC.
The side AB is common to the
triangles ABC and BAC.
Since all three of the corresponding sides of the
triangles ABC and BAC are of equal length,
these two triangles are congruent, in accordance
to the postulate 3 (SSS) of the triangle
congruency.
Hence, the corresponding
angles BAC and ABC are congruent.
The proof is completed.
Figure 1. To the
Theorem 1
Thus we proved that in isosceles triangle two angles opposite to the
equal sides are congruent.
Theorem 2
If in a triangle two angles are congruent, then the sides opposite

11. to these angles are of equal length.
Proof
Let ABC be a triangle with congruent
angles BAC and ABC (Figure
2).
We need to prove that angles BAC and ABC are
congruent.
Consider the triangle BAC.
The angle BAC of the triangle ABC corresponds
to the angle ABC of the triangle BAC.
The angle ABC of the triangle ABC corresponds
to the angle BAC of the triangle BAC.
The side AB is common to the
triangles ABC and BAC.
Since two angles and the included sides of the
triangles ABC and BAC are congruent,
these two triangles are congruent, in accordance
to the postulate 2 (ASA) of the triangle
congruency .
Hence, the corresponding sides AC and BC are of
equal length.
The proof is completed.
Figure 2. To the
Theorem 2
Thus we proved that in isosceles triangle two sides opposite to the
congruent angles are of equal length.
BISECTORS
A line which cuts an angle into two equal halves. For every

12. angle, there exists a line that divides the angle into two equal
parts. This line is known as the angle bisector. In a triangle, there
are three such lines. Three angle bisectors of a triangle meet at a
point called the incenter of the triangle.
The perpendicular bisectors of the sides of a triangle intersect at a point
called the circumcenter of the triangle, which is equidistant from the vertices
of the triangle.
Point G is the circumcenter of ABC.
APPLICATION AND EXAMPLES
Example 1: Let ABCD be a parallelogram and AC be one of its diagonals.
What can you say about triangles ABC and CDA? Explain your answer.
Solution to Example 1:

13.  In a parallelogram, opposite sides are congruent. Hence sides
BC and AD are congruent, and also sides AB and CD are congruent.
 In a parallelogram opposite angles are congruent. Hence angles
ABC and CDA are congruent.
 Two sides and an included angle of triangle ABC are congruent to
two corresponding sides and an included angle in triangle CDA.
According to the above postulate the two triangles ABC and CDA are
congruent.
Example 2: Let ABCD be a square and AC be one of its diagonals.
What can you say about triangles ABC andCDA? Explain your
answer
Solution to Example 2:
 In a square, all four sides are congruent. Hence sides AB and CD are
congruent, and also sides BC and DA are congruent
 The two triangles also have a common side: AC. Triangles ABC has
three sides congruent to the corresponding three sides in triangle
CDA. According to the above postulate the two triangles are
congruent. The triangles are also right triangles and isosceles.
Example 3: ABC is an isosceles triangle. BB' is the angle bisector. Show
that triangles ABB' and CBB' are congruent.

14. Solution to Example 3:
 Since ABC is an isosceles triangle its sides AB and BC are congruent
and also its angles BAB' and BCB' are congruent. Since BB' is an
angle bisector, angles ABB' and CBB' are congruent.
Two angles and an included side in triangles ABB' are congruent to
two corresponding angles and one included side in triangle CBB'.
According to the above postulate triangles ABB' and CBB' are
congruent.
Example 4: What can you say about triangles ABC and QPR shown
below.
Solution to Example 4:
 In triangle ABC, the third angle ABC may be calculated using the
theorem that the sum of all three angles in a triangle is equal to
180 derees. Hence
angle ABC = 180 - (25 + 125) = 30 degrees
 The two triangles have two congruent corresponding angles and
one congruent side.

15. angles ABC and QPR are congruent. Also angles BAC and PQR
are congruent. Sides BC and PR are congruent.
 Two angles and one side in triangle ABC are congruent to two
corresponding angles and one side in triangle PQR. According to
the above theorem they are congruent.
Example 5: Show that the two right triangles shown below are congruent.
Solution to Example 5:
 We first use Pythagora's theorem to find the length of side AB in
triangle ABC.
length of AB = sqrt [5 2 - 3 2] = 4
 One side and the hypotenuse in triangle ABC are congruent to a
corresponding side and hypotenuse in the right triangle A'B'C'.
According to the above theorem, triangles ABC and B'A'C' are
congruent.
TERMINAL EXERCISE
1.

16. 2.
3.
4.