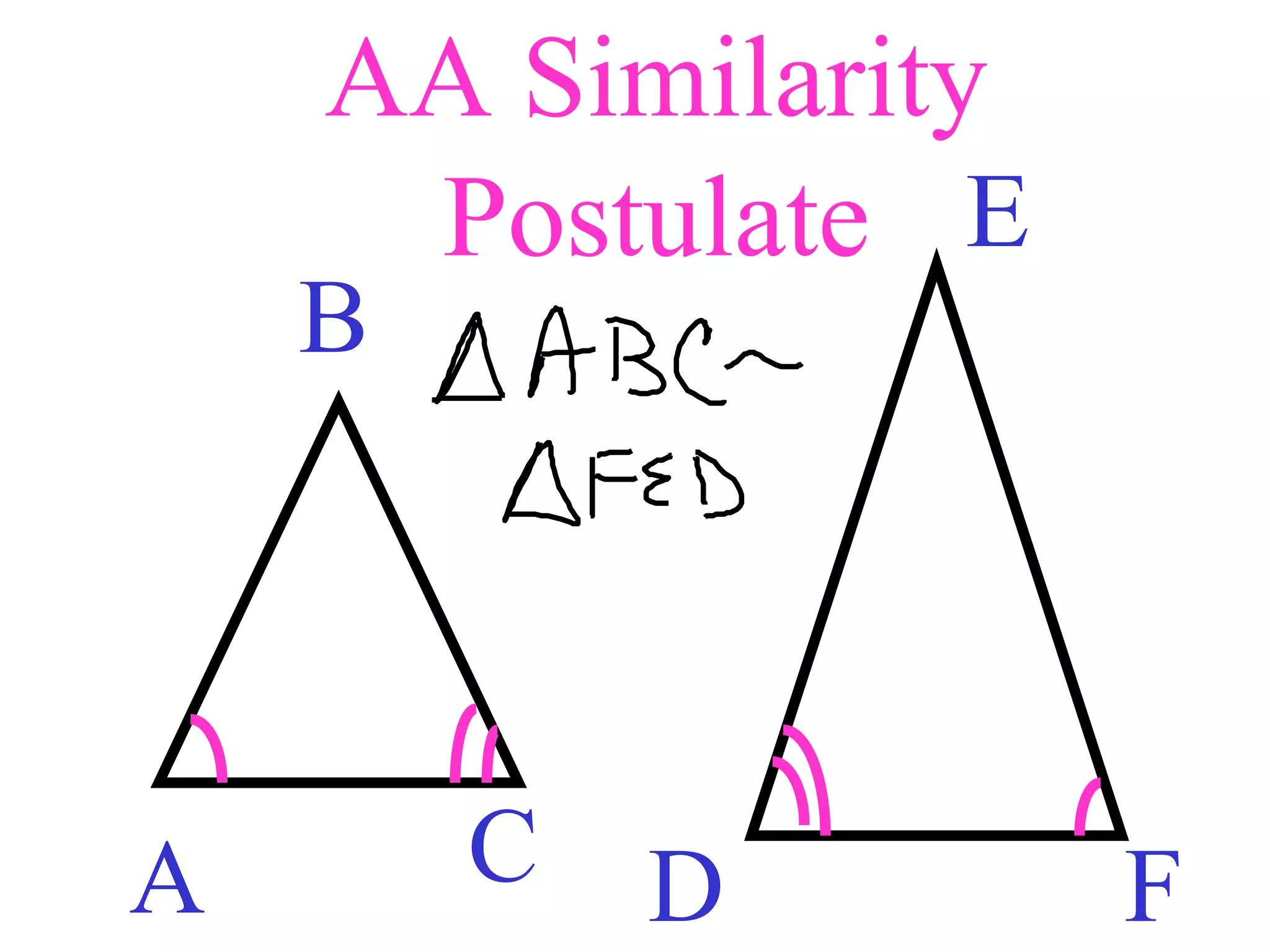
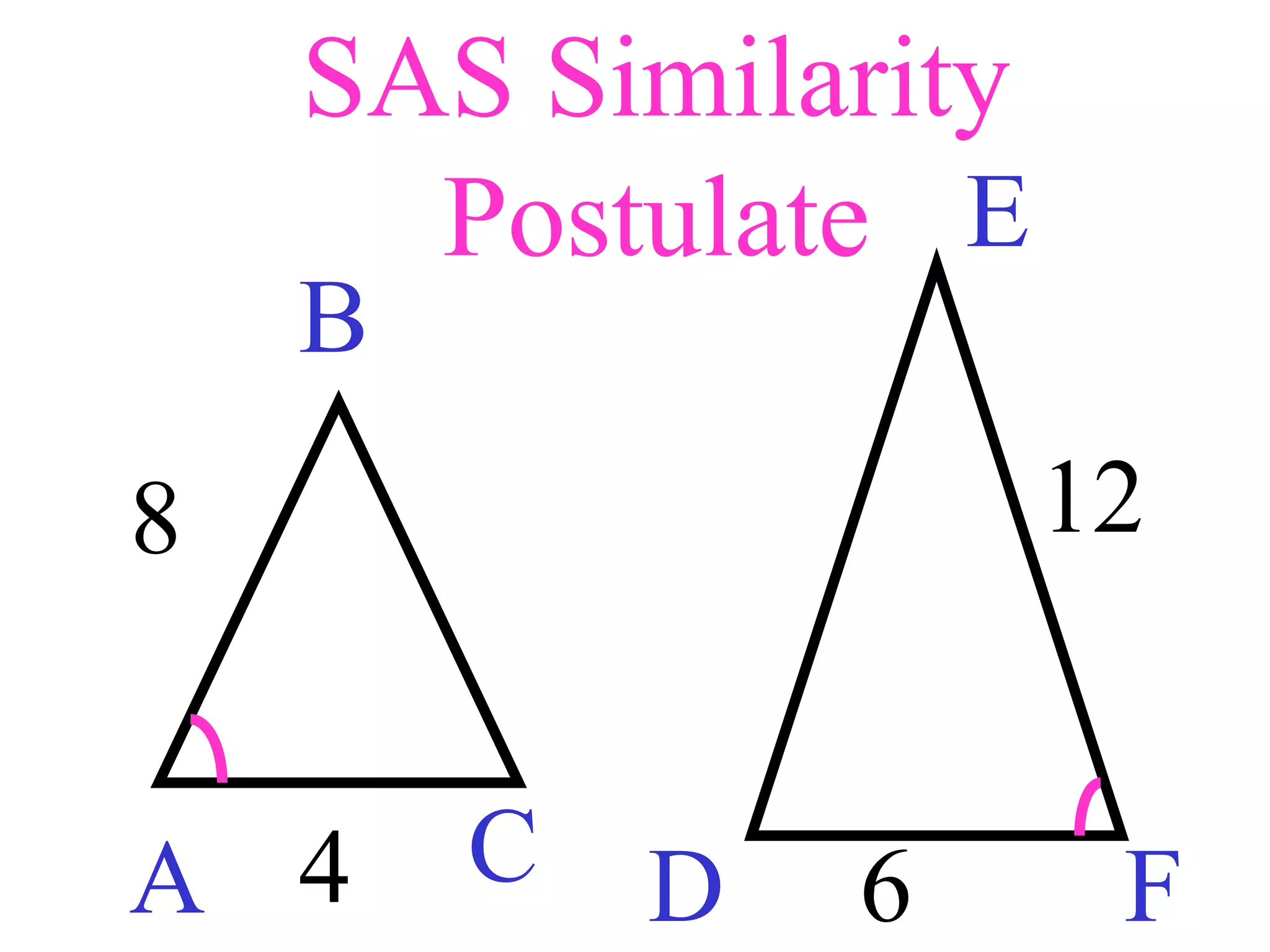
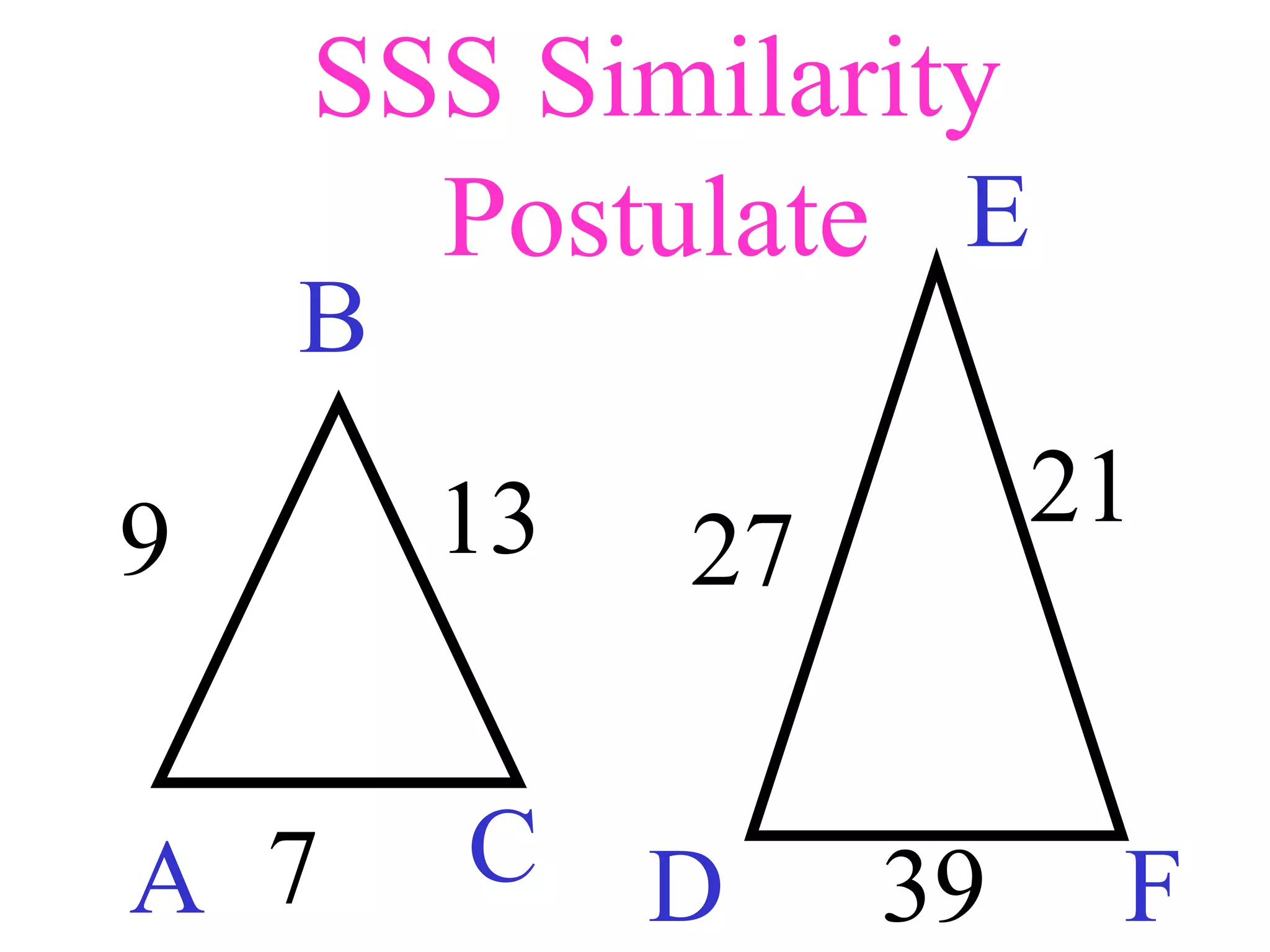
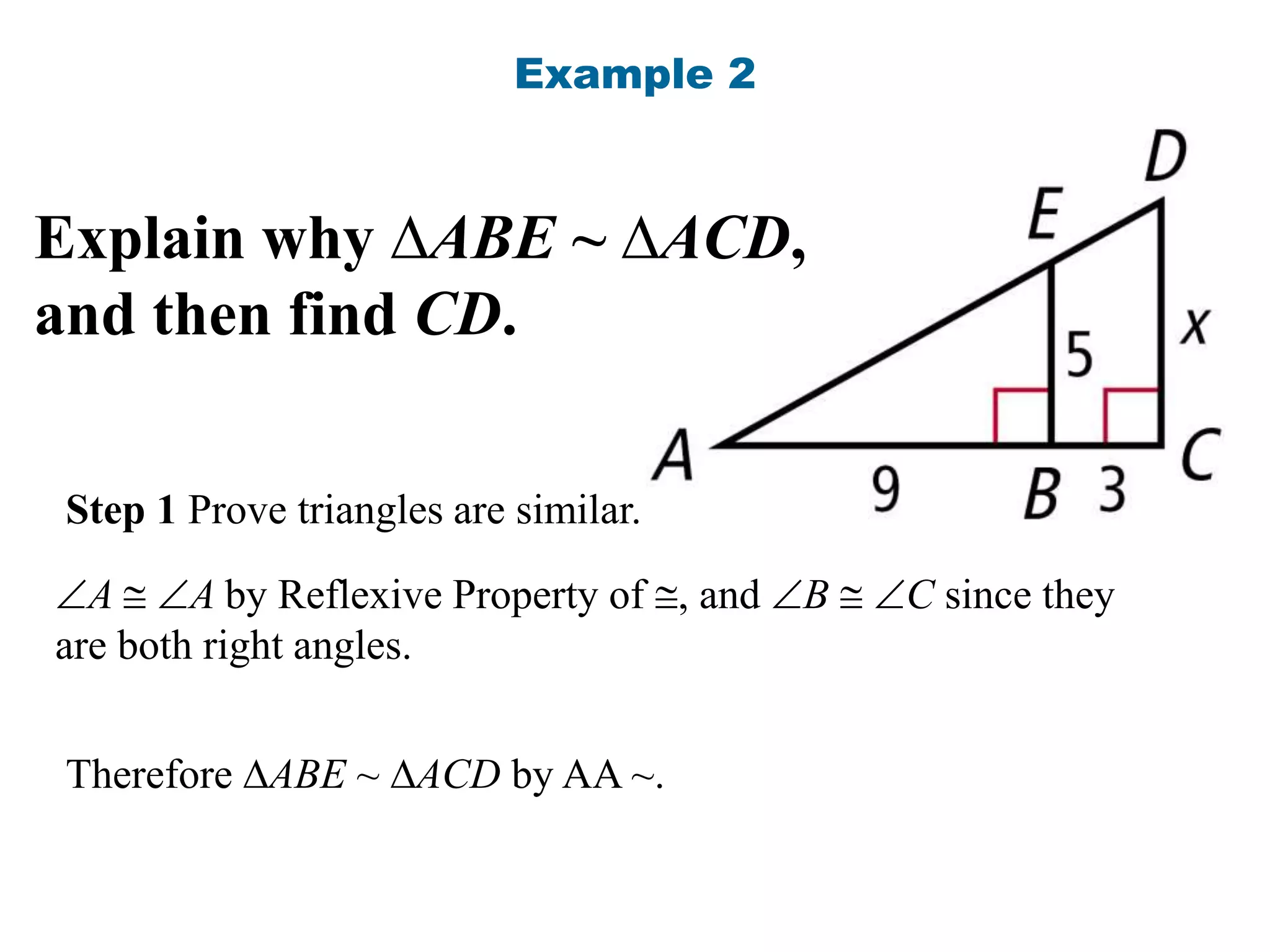
The document contains information about using similarity postulates to determine if triangles are similar and find unknown side lengths. It provides examples of using the AA, SAS, and SSS similarity postulates to show triangles are similar. It also shows using proportional sides to find missing lengths. The objective is for students to use similarity postulates to decide if triangles are similar and find unknowns.

1. #3.19 Geo. Drill 3/5/14
• Given that the following two
pentagons are similar, find x.
8
12
4
6
x
14
5
4
10

2. #3.19 Geo. Drill 3/5/14
• Given that the following two
pentagons are similar, find x.
8
12
4
6
x
14
5
4
10

3. Geometry Drill
•Can you list the
5 ways to prove
triangles
congruent

4. Objective
• Students will use the
similarity postulates to
decide which triangles
are similar and find
unknowns.

5. Congruence vs.
Similarity
•Congruence implies
that all angles and
sides have equal
measure whereas...

6. Congruence vs.
Similarity
•Similarity implies
that only the angles
are of equal measure
and the sides are
proportional

7. AA Similarity
Postulate
•Two triangles are
similar if two pairs
of corresponding
angles are congruent

8. AA Similarity
Postulate E
B
A
C
D
F

9. SAS Similarity
Postulate
•Two triangles are similar if
two pairs of corresponding
sides are proportional and
the included angles are
congruent

10. SAS Similarity
Postulate E
B
12
8
A 4
C
D
6
F

11. SSS Similarity
Postulate
•Two triangles are similar if
all three pairs of
corresponding sides are
proportional.

12. SSS Similarity
Postulate E
B
9
13
A 7
C
21
27
D
39
F

13. Example 1
•∆APE ~ ∆DOG. If the
perimeter of ∆APE is 12
and the perimeter of ∆DOG
is 15 and OG=6, find the
PE.

14. Example 2
Explain why ∆ABE ~ ∆ACD,
and then find CD.
Step 1 Prove triangles are similar.
A  A by Reflexive Property of , and B  C since they
are both right angles.
Therefore ∆ABE ~ ∆ACD by AA ~.

15. Step 2 Find CD.
Corr. sides are proportional.
Seg. Add. Postulate.
x(9) = 5(3 + 9)
9x = 60
60 20
x

9
3
Substitute x for CD, 5 for
BE, 3 for CB, and 9 for BA.
Cross Products Prop.
Simplify.
Divide both sides by 9.

16. Explain why ∆RSV ~ ∆RTU and then
find RT.
Step 1 Prove triangles are similar.
It is given that S  T.
R  R by Reflexive Property of .
Therefore ∆RSV ~ ∆RTU by AA ~.

17. Check It Out! Example 3 Continued
Step 2 Find RT.
Corr. sides are proportional.
Substitute RS for 10, 12 for TU, 8 for
SV.
RT(8) = 10(12)
8RT = 120
RT = 15
Cross Products Prop.
Simplify.
Divide both sides by 8.

18. Writing Proofs with Similar Triangles
Given: 3UT = 5RT and 3VT = 5ST
Prove: ∆UVT ~ ∆RST

19. Example 4 Continued
Statements
Reasons
1. 3UT = 5RT
1. Given
2.
2. Divide both sides by 3RT.
3. 3VT = 5ST
3. Given.
4.
4. Divide both sides by3ST.
5. RTS  VTU
5. Vert. s Thm.
6. ∆UVT ~ ∆RST
6. SAS ~ Steps 2, 4, 5

20. Given: M is the midpoint of JK. N is the
midpoint of KL, and P is the midpoint of JL.
Prove: ∆JKL ~ ∆NPM

21. Statements
Reasons
1. M is the mdpt. of JK,
N is the mdpt. of KL,
and P is the mdpt. of JL.
1. Given
2.
2. ∆ Midsegs. Thm
3.
4. ∆JKL ~ ∆NPM
3. Div. Prop. of =.
4. SSS ~

22. Example 5: Engineering Application
The photo shows a gable roof. AC || FG. ∆ABC ~ ∆FBG.
Find BA to the nearest tenth of a foot.
From p. 473, BF  4.6 ft.
BA = BF + FA
 6.3 + 17
 23.3 ft
Therefore, BA = 23.3 ft.

23. Check It Out! Example 5
What if…? If AB = 4x, AC = 5x, and BF = 4, find FG.
Corr. sides are proportional.
Substitute given quantities.
4x(FG) = 4(5x)
FG = 5
Cross Prod. Prop.
Simplify.

24. Conclusion
•Similarity
•AA
•SAS
•SSS

25. Classwork/Homework
•Page 474-475 #’s 110, 17,18, 23, 24,
44-46