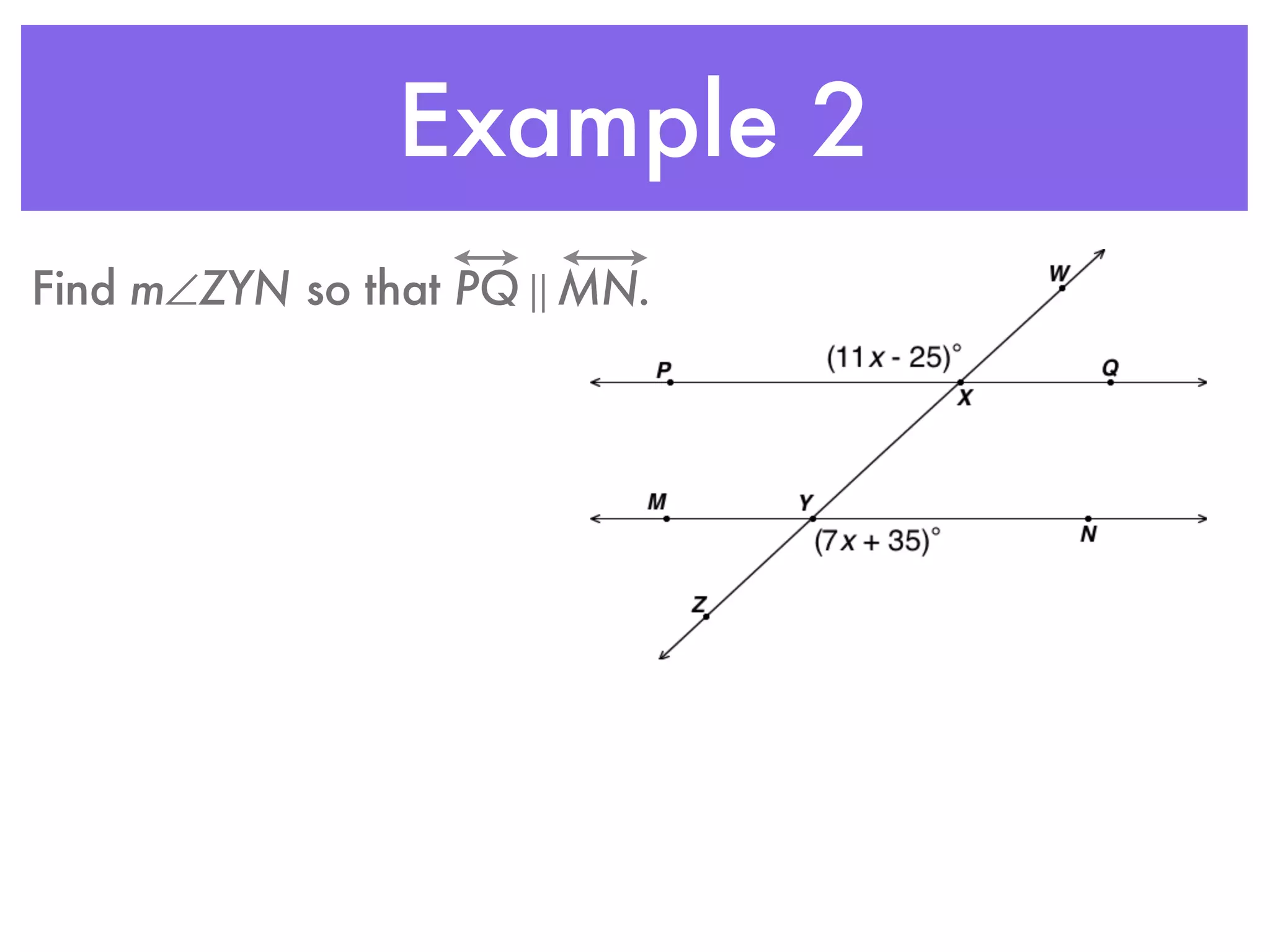
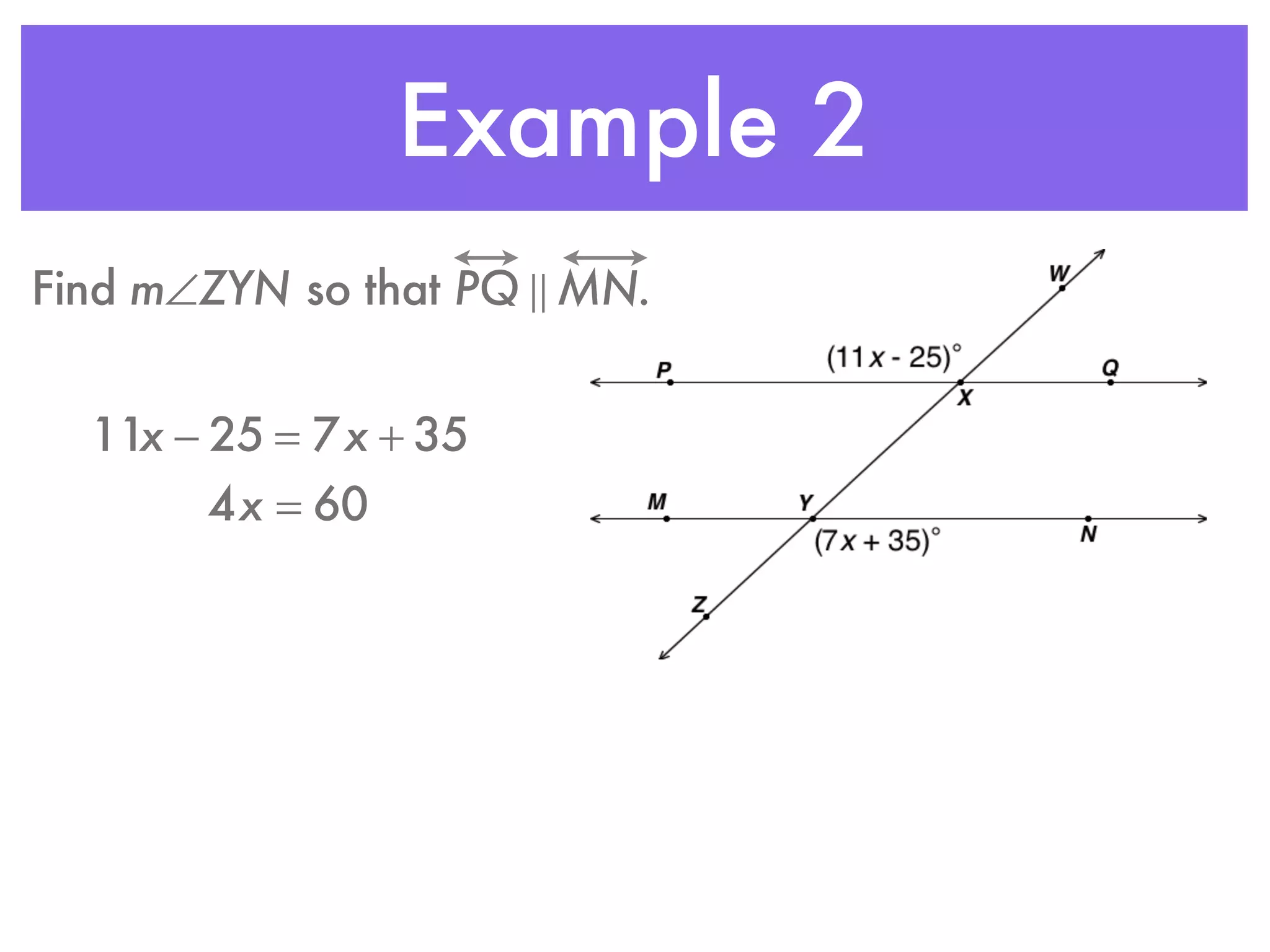
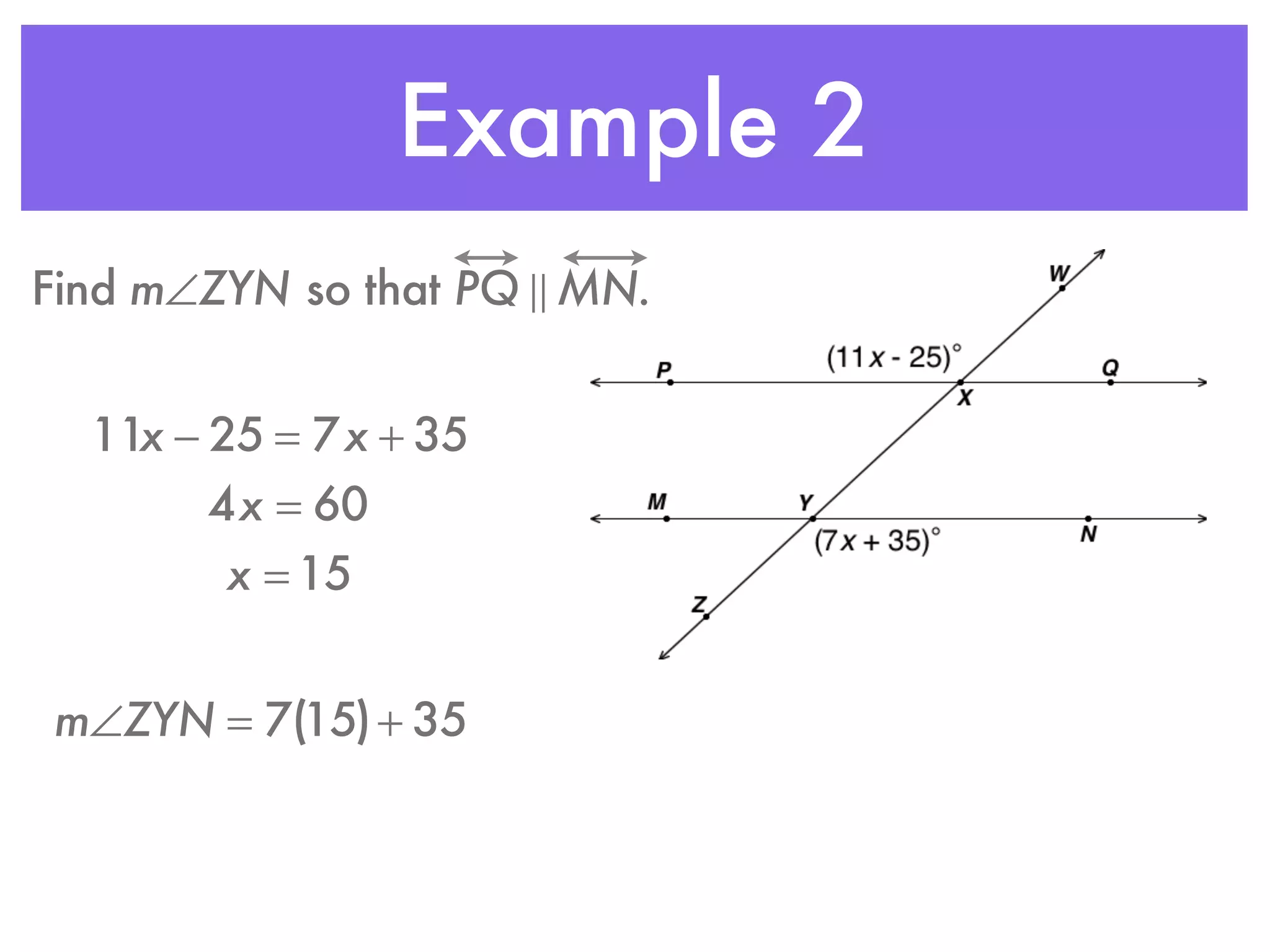
This document discusses proving that lines are parallel. It defines six postulates and theorems related to parallel lines, including the converse of corresponding angles, alternate exterior angles, consecutive interior angles, and alternate interior angles. An example problem demonstrates using the corresponding angles converse to show that two lines are parallel based on congruent corresponding angles. A second example finds the measure of an angle given that two lines are parallel based on the alternate interior angles theorem.

1. Section 2-9
Proving Lines Parallel

2. Essential Questions
• How do you recognize angle pairs that
occur with parallel lines?
• How do you prove that two lines are
parallel?

3. Postulates & Theorems
1. Converse of Corresponding Angles Postulate

4. Postulates & Theorems
1. Converse of Corresponding Angles Postulate
If two lines are cut by a transversal so that
corresponding angles are congruent, then the lines are
parallel.

5. Postulates & Theorems
2. Parallel Postulate

6. Postulates & Theorems
2. Parallel Postulate
If given a line and a point not on the line, then there
exists exactly one line through the point that is parallel
to the given line.

7. Postulates & Theorems
3. Alternate Exterior Angles Converse

8. Postulates & Theorems
3. Alternate Exterior Angles Converse
If two lines in a plane are cut by a transversal so that a
pair of alternate exterior angles is congruent, then the
two lines are parallel.

9. Postulates & Theorems
4. Consecutive Interior Angles Converse

10. Postulates & Theorems
4. Consecutive Interior Angles Converse
If two lines in a plane are cut by a transversal so that a
pair of consecutive interior angles is supplementary,
then the lines are parallel.

11. Postulates & Theorems
5. Alternate Interior Angles Converse

12. Postulates & Theorems
5. Alternate Interior Angles Converse
If two lines in a plane are cut by a transversal so that a
pair of alternate interior angles is congruent, then the
two lines are parallel.

13. Postulates & Theorems
6. Perpendicular Transversal Converse

14. Postulates & Theorems
6. Perpendicular Transversal Converse
In a plane, if two lines are perpendicular to the same
line, then they are parallel.

15. Example 1
Given the following information, is it possible to prove
that any of the lines shown are parallel? If so, state the
postulate or theorem that justifies your answer.
a. ∠1≅ ∠3

16. Example 1
Given the following information, is it possible to prove
that any of the lines shown are parallel? If so, state the
postulate or theorem that justifies your answer.
a. ∠1≅ ∠3
a ! b since these
congruent angles are
also corresponding,
the Corresponding
Angles Converse
holds

17. Example 1
Given the following information, is it possible to prove
that any of the lines shown are parallel? If so, state the
postulate or theorem that justifies your answer.
b. m∠1= 103° and m∠4 = 100°

18. Example 1
Given the following information, is it possible to prove
that any of the lines shown are parallel? If so, state the
postulate or theorem that justifies your answer.
b. m∠1= 103° and m∠4 = 100°
are
alternate interior
angles, but not
congruent, so a is not
parallel to c
∠1and ∠4

19. Example 2
Find m∠ZYN so that PQ ! MN.

20. Example 2
Find m∠ZYN so that PQ ! MN.
11x − 25 = 7x + 35

21. Example 2
Find m∠ZYN so that PQ ! MN.
11x − 25 = 7x + 35
4x = 60

22. Example 2
Find m∠ZYN so that PQ ! MN.
11x − 25 = 7x + 35
4x = 60
x = 15

23. Example 2
Find m∠ZYN so that PQ ! MN.
11x − 25 = 7x + 35
4x = 60
x = 15
m∠ZYN = 7(15)+ 35

24. Example 2
Find m∠ZYN so that PQ ! MN.
11x − 25 = 7x + 35
4x = 60
x = 15
m∠ZYN = 7(15)+ 35 = 105 + 35

25. Example 2
Find m∠ZYN so that PQ ! MN.
11x − 25 = 7x + 35
4x = 60
x = 15
m∠ZYN = 7(15)+ 35 = 105 + 35 = 140

26. Example 2
Find m∠ZYN so that PQ ! MN.
11x − 25 = 7x + 35
4x = 60
x = 15
m∠ZYN = 7(15)+ 35 = 105 + 35 = 140
m∠ZYN = 140°