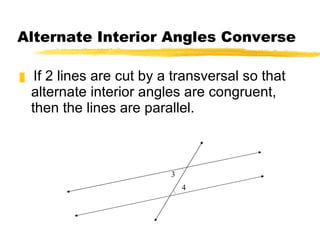
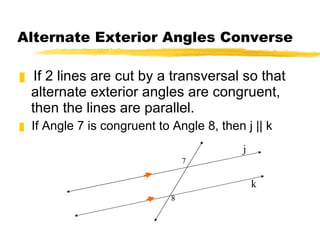
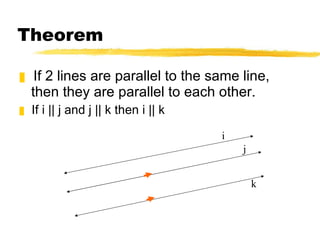
This document discusses different ways to prove that two lines are parallel using properties of parallel lines cut by a transversal. It introduces the converse theorems for corresponding angles, alternate interior angles, consecutive interior angles, and alternate exterior angles being congruent to show lines are parallel. It also presents two additional theorems: if two lines are parallel to the same line then they are parallel to each other, and if two lines are perpendicular to the same line then they are parallel to each other. The document provides example problems and homework assignments to practice these concepts.

1. 3.4 & 3.5 Proving Lines are Parallel Objectives: - Prove that 2 lines are parallel - Use properties of parallel lines to solve real life problems

2. Corresponding Angles Converse If lines are cut by a transversal so that corresponding angles are congruent, then the lines are parallel.

3. Alternate Interior Angles Converse If 2 lines are cut by a transversal so that alternate interior angles are congruent, then the lines are parallel. 3 4

4. Consecutive Interior Angles Converse If lines are cut by a transversal so that consecutive interior angles are supplementary, then the lines are parallel. If Angle 5 + Angle 6 = 180, then j || k 5 6 k j

5. Alternate Exterior Angles Converse If 2 lines are cut by a transversal so that alternate exterior angles are congruent, then the lines are parallel. If Angle 7 is congruent to Angle 8, then j || k 7 8 k j

6. Do examples on p. 151-152 Do p. 153 1-9, p. 154 19 Look at Example 1, p. 157

7. Theorem If 2 lines are parallel to the same line, then they are parallel to each other. If i || j and j || k then i || k k j i

8. Another theorem In a plane, if 2 lines are perpendicular to the same line, then they are parallel to each other. If m | p and n | p then m || n m n p

9. Do examples on p. 158 Do p. 160 1-20, 30, 31, 39 Homework: Worksheets